Three particles of equal masses are initial at the vertices of equilateral triangle of side 2√3m in horizontal plane. They start moving towards centroid O with equal speed 2m/sec. After collision at O, A stops and C retraces its path with same speed. Distance between B and C just after one second of the collision is αm. Here α is an integer. Find α. 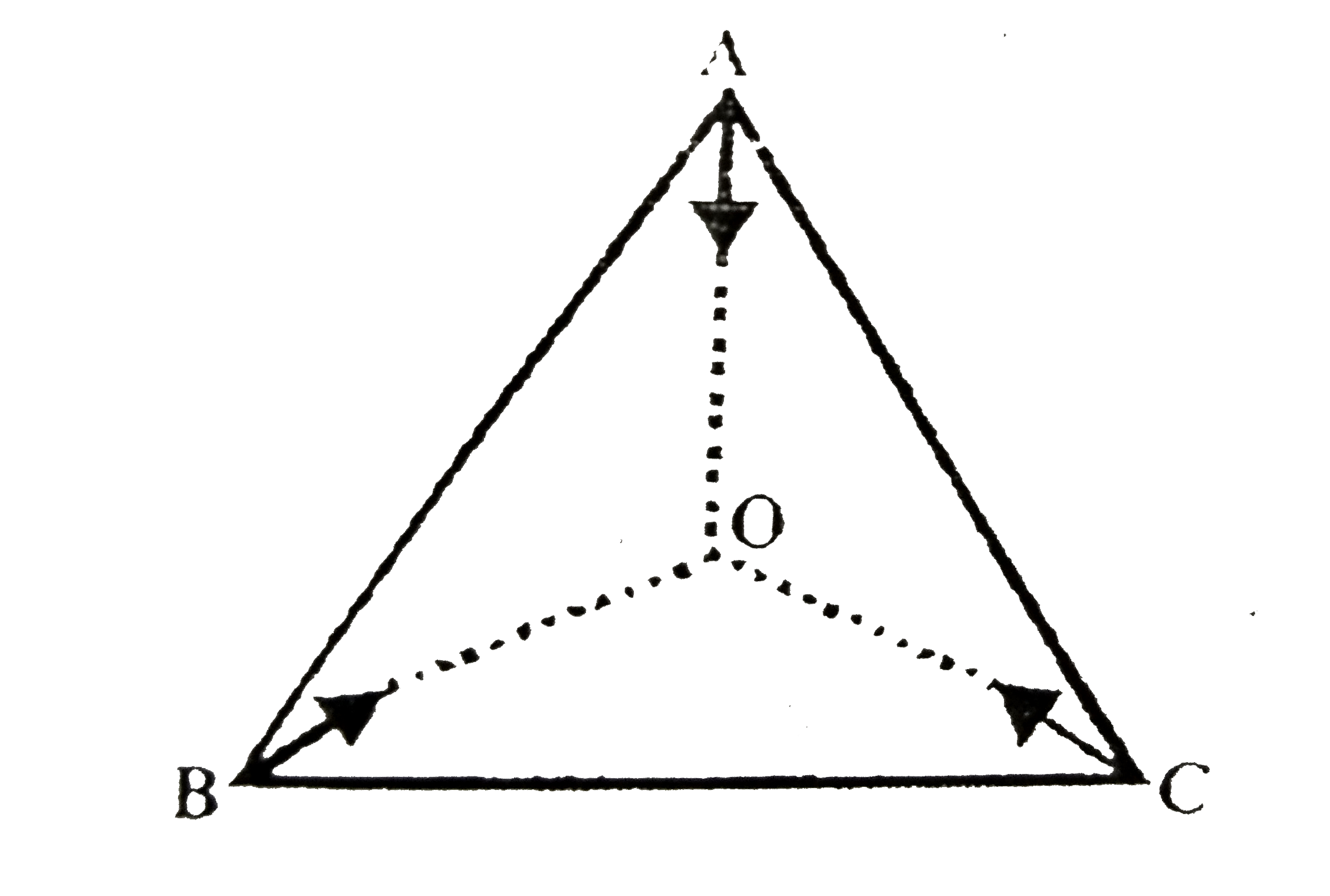
The correct Answer is:4
Before collision, linear momentum of the system is zero. Therefore, after collision momentum of B will be equal and opposite to momentum of C (since PA=0)
Topper's Solved these Questions
- TEST PAPERSBook:RESONANCE ENGLISHChapter:TEST PAPERSExercise:PART - II PHYSICS
Explore 106 Videos
- SIMPLE HARMONIC MOTION Book:RESONANCE ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:Advanced Level Problems
Explore 13 Videos
- TEST SERIESBook:RESONANCE ENGLISHChapter:TEST SERIESExercise:PHYSICS
Explore 130 Videos
Similar Questions
Three particles A, B and C of equal mass move with equal speed V along the medians of an equilateral triangle as shown in hgure. They collide at the centroid G of the triangle. After the collision, A comes to test, B retraces its path with the speed V. What is the velocity of C ?
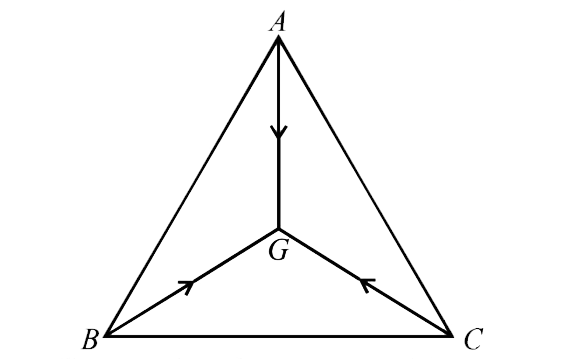
View SolutionThree particles A, B and C of equal mass move with equal speed 10 m/sec along the medians of an equilateral triangle as shown in the figure. They collide at the centroid G of the triangle. After the collision, A comes to rest, B retraces its path with the speed 10 m/sec. The velocity of C is _______ m/sec.

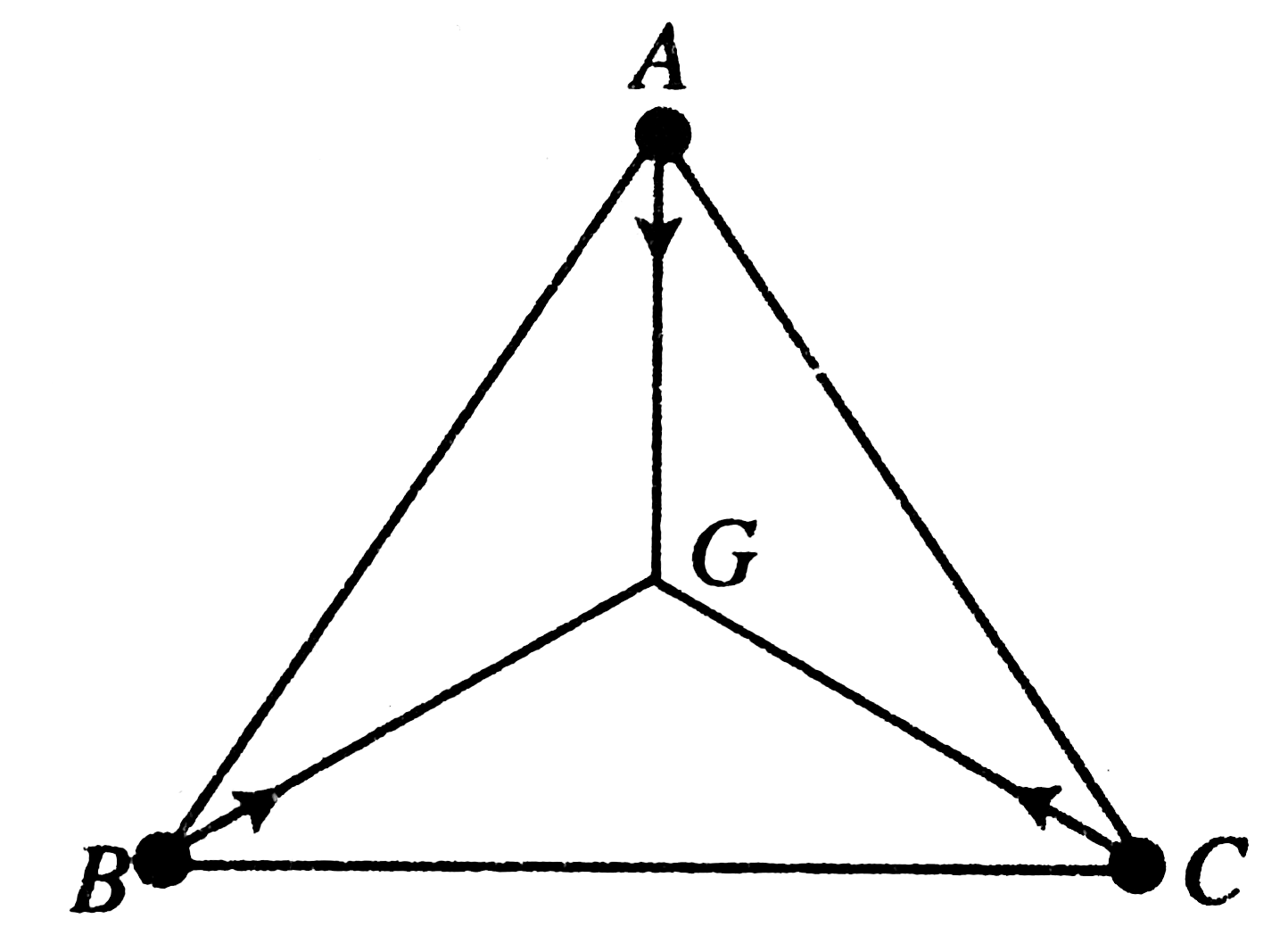
View SolutionThree particlesA,B and C of equal mass move with equal speed V=5ms−1 along the medians of an equilateral triangle as shown in the figure. They collide at the centroid G of the triangle. After the collision, A comes to rest, B retraces its path with the speed V=5ms−1. What is the speed of C?
View SolutionThree particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
View SolutionTwo particles A and B of equal size but of masses mkg and 2mkg are moving directly towards each other with speeds 21m/s and 4m/s respectively. After collision, A moves with a speed of 1m/s in the original direction. Then:
View SolutionThree identical particles are located at the vertices of an equilateral triangle. Each particle moves along a meridian with equal speed towards the centroid and collides inelastically. (a) all the three particles will bounce back along the meridians with lesser speed. (b) all the three particles will become stationary. (c) all the particles will continue to move in their original directions but with lesser speed (d) nothing can be said
View SolutionLet there are three equal masses situated at the vertices of an equilateral triangle, as shown in Fig. Now particle A starts with a velocity v1 towards line AB, particle B starts with the velocity v2, towards line BC and particle C starts with velocity v3 towards line CA. Find the displacement of the centre of mass of the three particles A,B and C after time t. What would it be if v1=v2=v3?
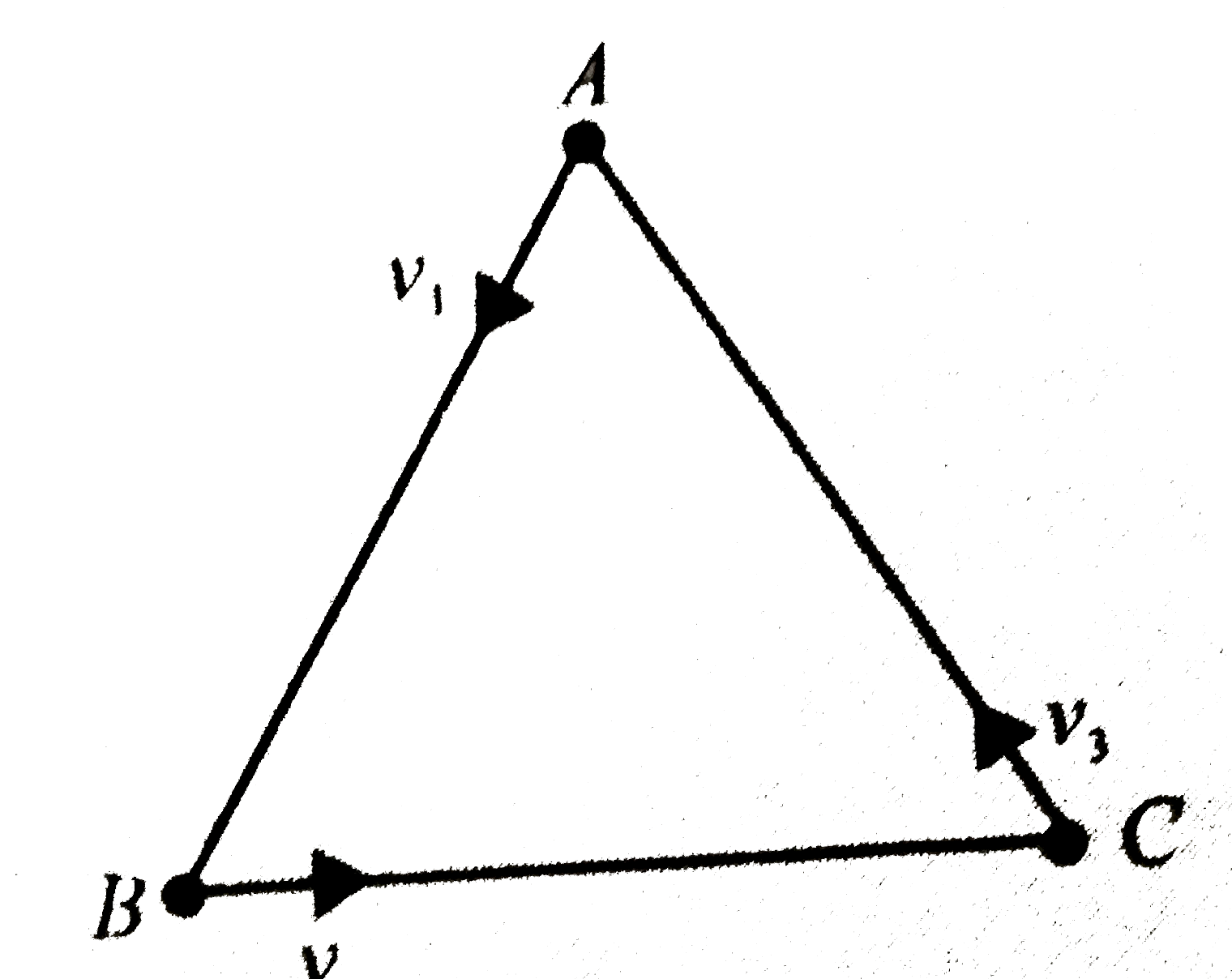
View SolutionThree equal masses of 1 kg each are placed at the vertices of an equilateral triangle and other particle of mass 2kg is placed on centroid of triangle which is at a distance of √2 m from each of the vertices of the triangle .The force in newton , acting on the particle of mass 2 kg is
View SolutionA bomb initially at rest at a height of 40 m above the ground suddenly explodes into two identical fragments. One of them starts moving vertically downwards with an initial speed of 10 m/s. If acceleration due to gravity is 10 m/s2, the separation between the fragments, 2 seconds after the explosion is
View SolutionTwo particles of mass 2m and m moving with speed v and 2v respectively pependicular to each other collides perfectly inelastically, then

Find the angle with the horizontal to which the particles move after collision.
View Solution

