Two particles A and B of equal size but of masses mkg and 2mkg are moving directly towards each other with speeds 21m/s and 4m/s respectively. After collision, A moves with a speed of 1m/s in the original direction. Then:
The velocity of B after collisionis 6 m/s opposite its direction of mation before collision.
The coefficient of restitution is 0.2
The loss of kinetic energy due to collision is 200 J
The impulse of the force between the two balls is 40 N-s
To solve the problem step by step, we will apply the principles of conservation of momentum and the definition of the coefficient of restitution.
Step 1: Understand the Problem
We have two particles A and B with masses m and 2m, moving towards each other with speeds 21ms and 4ms, respectively. After the collision, particle A moves at 1ms in its original direction, and we need to find the speed of particle B after the collision and the coefficient of restitution.
Step 2: Set Up the Conservation of Momentum Equation
According to the law of conservation of momentum:
\(
\text{Initial Momentum} = \text{Final Momentum}
\)
The initial momentum before the collision can be expressed as:
\(
m \cdot 21 + 2m \cdot (-4) = m \cdot 21 - 8m = 13m
\)
The final momentum after the collision is:
\(
m \cdot 1 + 2m \cdot V_{B2}
\)
Setting the initial momentum equal to the final momentum gives us:
\(
13m = m \cdot 1 + 2m \cdot V_{B2}
\)
Step 3: Solve for \( V_{B2} \)
Now, we can simplify the equation:
\(
13m = m + 2m \cdot V_{B2}
\)
Dividing through by \( m \) (assuming \( m \neq 0 \)):
\(
13 = 1 + 2V_{B2}
\)
Subtracting 1 from both sides:
\(
12 = 2V_{B2}
\)
Dividing by 2:
\(
V_{B2} = 6 \, \text{m/s}
\)
Step 4: Calculate the Coefficient of Restitution
The coefficient of restitution \( e \) is defined as:
\(
e = \frac{\text{Velocity of separation}}{\text{Velocity of approach}}
\)
The velocity of separation is:
\(
V_{B2} - V_{A2} = 6 - 1 = 5 \, \text{m/s}
\)
The velocity of approach is:
\(
V_{A1} + |V_{B1}| = 21 + 4 = 25 \, \text{m/s}
\)
Thus, the coefficient of restitution is:
\(
e = \frac{5}{25} = \frac{1}{5} = 0.2
\)
Final Results
- The speed of particle B after the collision \( V_{B2} = 6 \, \text{m/s} \).
- The coefficient of restitution \( e = 0.2 \).
We have two particles A and B with masses m and 2m, moving towards each other with speeds 21ms and 4ms, respectively. After the collision, particle A moves at 1ms in its original direction, and we need to find the speed of particle B after the collision and the coefficient of restitution.
According to the law of conservation of momentum:
\(
\text{Initial Momentum} = \text{Final Momentum}
\)
The initial momentum before the collision can be expressed as:
\(
m \cdot 21 + 2m \cdot (-4) = m \cdot 21 - 8m = 13m
\)
The final momentum after the collision is:
\(
m \cdot 1 + 2m \cdot V_{B2}
\)
Setting the initial momentum equal to the final momentum gives us:
\(
13m = m \cdot 1 + 2m \cdot V_{B2}
\)
Now, we can simplify the equation:
\(
13m = m + 2m \cdot V_{B2}
\)
Dividing through by \( m \) (assuming \( m \neq 0 \)):
\(
13 = 1 + 2V_{B2}
\)
Subtracting 1 from both sides:
\(
12 = 2V_{B2}
\)
Dividing by 2:
\(
V_{B2} = 6 \, \text{m/s}
\)
The coefficient of restitution \( e \) is defined as:
\(
e = \frac{\text{Velocity of separation}}{\text{Velocity of approach}}
\)
The velocity of separation is:
\(
V_{B2} - V_{A2} = 6 - 1 = 5 \, \text{m/s}
\)
The velocity of approach is:
\(
V_{A1} + |V_{B1}| = 21 + 4 = 25 \, \text{m/s}
\)
Thus, the coefficient of restitution is:
\(
e = \frac{5}{25} = \frac{1}{5} = 0.2
\)
- The speed of particle B after the collision \( V_{B2} = 6 \, \text{m/s} \).
- The coefficient of restitution \( e = 0.2 \).
Similar Questions
Two steel balls A and B of mass 10 kg and 10 g rolls towards each other with 5m/s and 1 m/s respectively on a smooth floor. After collision, with what speed B moves [perfectly elastic collision]?
View SolutionTwo identical balls each of mass 4 kg are moving towards each other with speeds 2 m/s and 3 m/s respectively. They undergo head on perfectly elastic collision. Then impulse imparted by one ball on other is
View SolutionTwo balls of masses m each are moving at right angle to each other with velocities 6 m/s and 8 m/s respectively. If collision between them is perfectly inelastic, the velocity of combined mass is
View SolutionTwo particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
View SolutionTwo particles of mass 1kg and 2kg are moving along the same line with speeds 2m/s and 4m/s respectively. Calculate the speed of the centre of mass of the system if both the particles are moving in the same direction.
View SolutionTwo particles of mass 1kg and 2kg are moving along the same line with speeds 2m/s and 4m/s respectively. Calculate the speed of the centre of mass of the system if both the particles are moving in the same direction.
View SolutionTwo balls of masses 2kg and 4kg are moved towards each other with velocities 4m/s and 2m/s, respectively, on a frictionless surface. After colliding, the 2kg ball returns back with velocity 2m/s. then find
a. velocity of the 4kg after collision
b. coefficient of restitution e,
c. impulse of deformation JD
d. maximum potential energy of deformation,
e. impulse of reformation JR
View SolutionTwo particles of masses 2kg and 4kg are approaching towards each other with ccelerations 1m/s2 and 2m/s2, respectively, on a smooth horizontal suface. Then find the acceleration of centre of mass of the system and direction of acceleration of CM.
View SolutionTwo particles of masses m1=6kg&m2=4kg move towards each other with u1=3m/sec&u2=6m/sec respectively. If they collide elastically, find the impulse of the particles.
View SolutionTwo particles A and B of masses 2kg and 3kg moving on a smooth horizontal surface with speed 1m/s and 2m/s collides perfectly inelastically, then
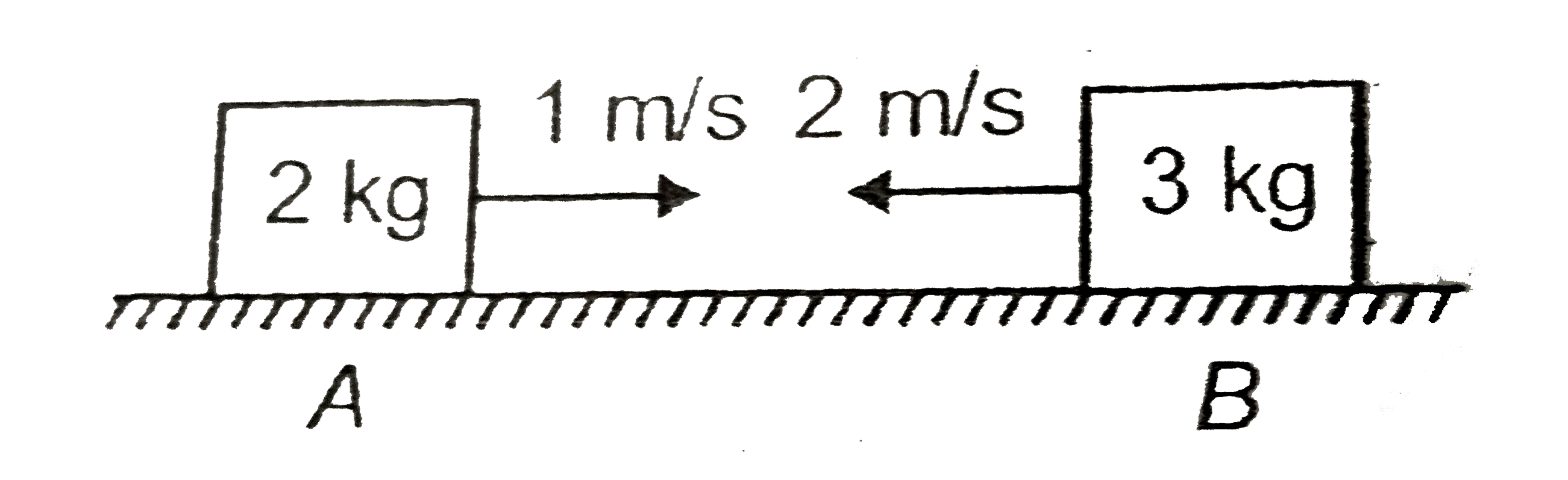
View Solution

