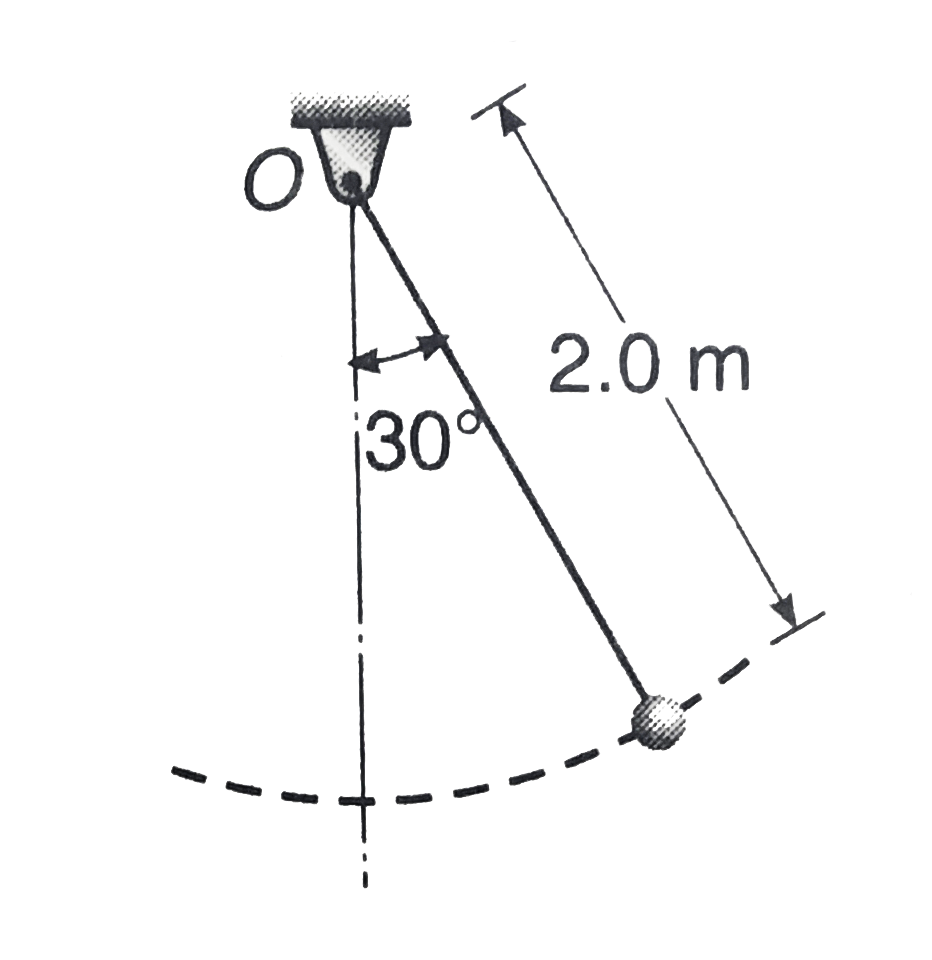
The bob of the pendulum shown in figure describes an arc of a circle in a vertical plane. If the tension in the cord is 2.5 times the weight of the bob for the position shown. Find the velocity and the acceleration of the bob in that position.
16.75ms−1,5.66ms−2
5.66ms−1,16.75ms−2
2.88ms−1,16.75ms−2
5.66ms−1,8.34ms−2
The correct Answer is:A, B
2.5mg−mgcos30∘=mv2r
:. 11.63g=v2r=v22
v=5.66m/s
Fnet=√(2.5mg)2+(mg)2+(2)(2.5mg)(mg)cos150∘
=1.7mg
anet=Fnetm=1.7g≈16.75m/s2

Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Level 2 Single Correct
Explore 18 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Level 2 More Than One Correct
Explore 5 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Level 1 Objective
Explore 14 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
The bob of a 0.2 m pendulum describs an arc of circle in a vertical plane. If the tension in the cord is √3 times the weight of the bob when the cord makes an angle 30∘ with the vertical, the acceleration of the bob in that position is g/n. Find value of n.
View SolutionTime period of small oscillation (in a verical plane normal to the plane of strings) of the bob in the arrangement shown will be
_E01_023_Q01.png)
View Solution
Knowledge Check
A pendulum bob is suspended inside a lift moving upward with constant velocity. If mass of the bob is 50 g then its weight inside the compartment is
AzeroB0.1 NC0.5 ND0.05 N
Let θ denote the angular displacement of a simple pendulum oscillating in a vertical plane. If the mass of the bob is m, the tension in the string is mgcosθ
View SolutionA simple pendulum suspended from the roof off a lift oscillates with frequency υ when the lift is at rest. If the lift falls freely under gravity, its frequency of oscillation becomes
View SolutionThe string of a pendulum is horizontal. The mass of the bob is m. Now the string is released. The tension in the string in the lowest position is -
View SolutionA bob of mass m is projected with a horizontal velocity v=√gl2 as shown in figure. In consequence, it moves in a circular path in a vertical plane by the inextensible string which passes over the smooth fixed peg. Find the maximum angle that the bob swings in the left hand side.
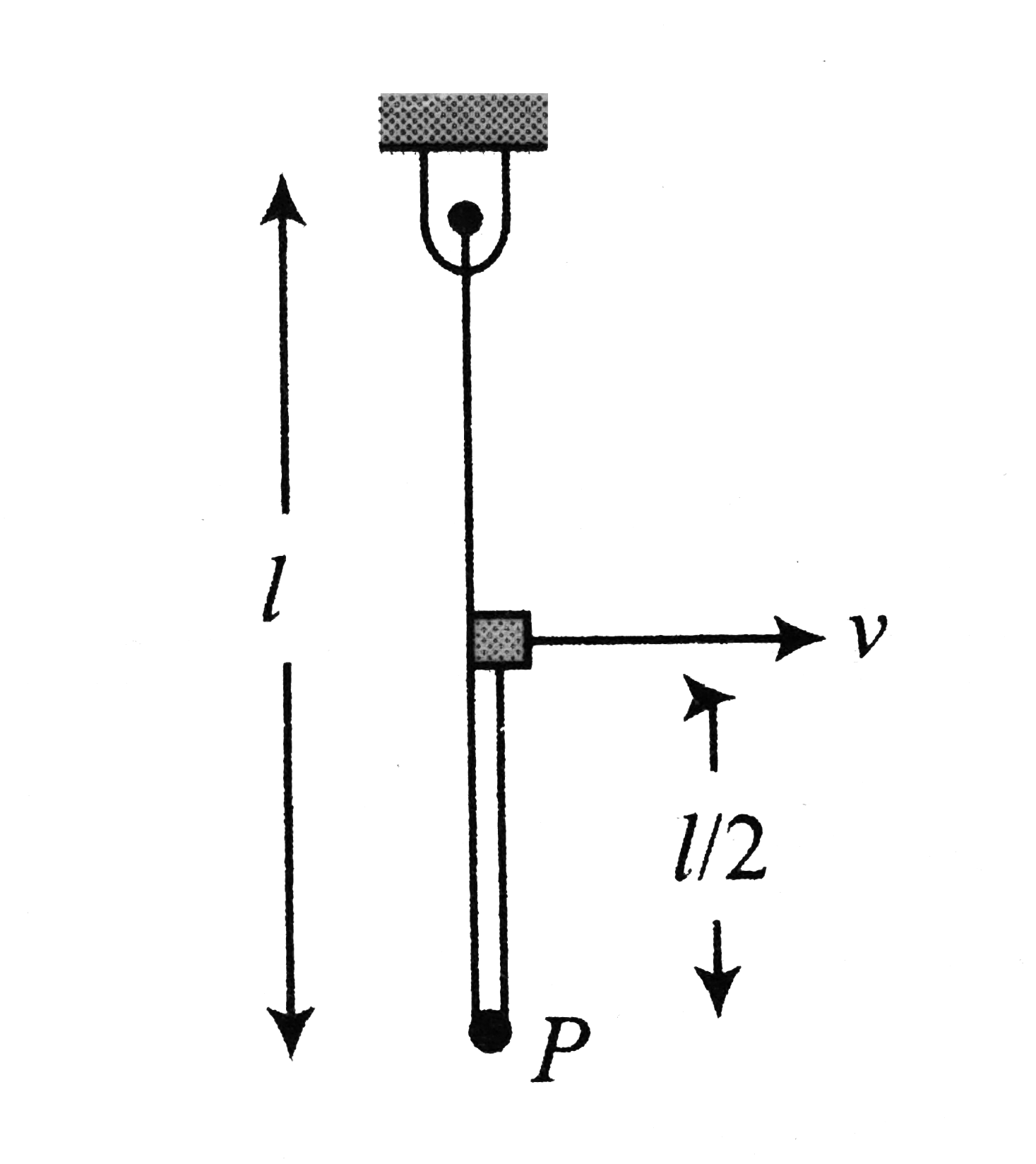
View SolutionSuppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.
View SolutionA simple pendulum is constructed by attaching a bob of mass m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionA simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View Solution