A ball tied to the end of the string swings in a verticla plane in a vertical circle under the influence of gravity.
When the string makes an angle 90∘ with the vertical, the tangential acceleration is zero and radial acceleration is somewhere between minimum and maximum
When the string makes an angle 90∘ with the vertical, the tangential acceleration is maximum and radial acceleration is somewhere between maximum and minimum
At no place in circular motion, tangential acceleration is equal to radial acceleration
When radial acceleration has its maximum value, the tangential acceleration is zero
The correct Answer is:B, D
To solve the problem regarding a ball tied to a string swinging in a vertical circle, we will analyze the forces acting on the ball at various points in its motion and determine the truth of the given statements.
1. Understanding the Forces:
- When the ball is at any point in the vertical circle, two main forces act on it: the tension (T) in the string and the gravitational force (mg) acting downward.
2. Identifying Components of Forces:
- At an angle θ from the vertical, the gravitational force can be resolved into two components:
- Radial (centripetal) component: mgcosθ
- Tangential component: mgsinθ
3. Centripetal Acceleration:
- The centripetal acceleration (a_c) required to keep the ball moving in a circle is given by:
ac=v2R
- At any point in the circle, the net force providing this centripetal acceleration is the difference between the tension and the radial component of the weight:
T−mgcosθ=mv2R
4. Tangential Acceleration:
- The tangential acceleration (a_t) is given by:
at=gsinθ
- This indicates that the tangential acceleration is maximum when θ = 90° (the lowest point in the swing).
5. Analyzing Specific Angles:
- At θ = 0° (top of the swing):
- Tangential acceleration: at=gsin0=0
- Centripetal acceleration: ac=v2R (maximum)
- At θ = 90° (lowest point):
- Tangential acceleration: at=gsin90=g (maximum)
- Centripetal acceleration: ac=T−mgR (depends on tension)
6. Evaluating the Statements:
- Statement 1: When the string makes an angle of 90 degrees with the vertical, tangential acceleration is zero.
- False: Tangential acceleration is maximum at this point.
- Statement 2: When the string makes an angle of 90 degrees with the vertical, the tangential acceleration is maximum and radial acceleration is somewhere between maximum and minimum.
- True: This is correct.
- Statement 3: At no place in circular motion is tangential acceleration equal to radial acceleration.
- False: They can be equal at certain points, such as at the highest point if conditions allow.
- Statement 4: When radial acceleration has its maximum value, tangential acceleration is zero.
- True: This is correct, as seen at the top of the swing.
7. Conclusion:
- The true statements are: Statement 2 and Statement 4.
- When the ball is at any point in the vertical circle, two main forces act on it: the tension (T) in the string and the gravitational force (mg) acting downward.
- At an angle θ from the vertical, the gravitational force can be resolved into two components:
- Radial (centripetal) component: mgcosθ
- Tangential component: mgsinθ
- The centripetal acceleration (a_c) required to keep the ball moving in a circle is given by:
ac=v2R
- At any point in the circle, the net force providing this centripetal acceleration is the difference between the tension and the radial component of the weight:
T−mgcosθ=mv2R
- The tangential acceleration (a_t) is given by:
at=gsinθ
- This indicates that the tangential acceleration is maximum when θ = 90° (the lowest point in the swing).
- At θ = 0° (top of the swing):
- Tangential acceleration: at=gsin0=0
- Centripetal acceleration: ac=v2R (maximum)
- At θ = 90° (lowest point):
- Tangential acceleration: at=gsin90=g (maximum)
- Centripetal acceleration: ac=T−mgR (depends on tension)
- Statement 1: When the string makes an angle of 90 degrees with the vertical, tangential acceleration is zero.
- False: Tangential acceleration is maximum at this point.
- Statement 2: When the string makes an angle of 90 degrees with the vertical, the tangential acceleration is maximum and radial acceleration is somewhere between maximum and minimum.
- True: This is correct.
- Statement 3: At no place in circular motion is tangential acceleration equal to radial acceleration.
- False: They can be equal at certain points, such as at the highest point if conditions allow.
- Statement 4: When radial acceleration has its maximum value, tangential acceleration is zero.
- True: This is correct, as seen at the top of the swing.
- The true statements are: Statement 2 and Statement 4.
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Level 2 Comprehension Based
Explore 5 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Level 2 Subjective
Explore 13 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Level 2 Single Correct
Explore 18 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
A stone of mass m tied to the end of a string, is whirled around in a horizontal circle. (Neglect the force due to gravity). The length of the string is reduced gradually keeping the angular momentum of the stone about the centre of the circle constant. Then, the tension in the string is given by T=Arn where A is a constant, r is the instantaneous radius of the circle and n=....
View SolutionA ball attached to one end of a string swings in a vertical plane such that its acceleration at point A (extreme position) is equal to its acceleration at point B (mean position), The angle θ is
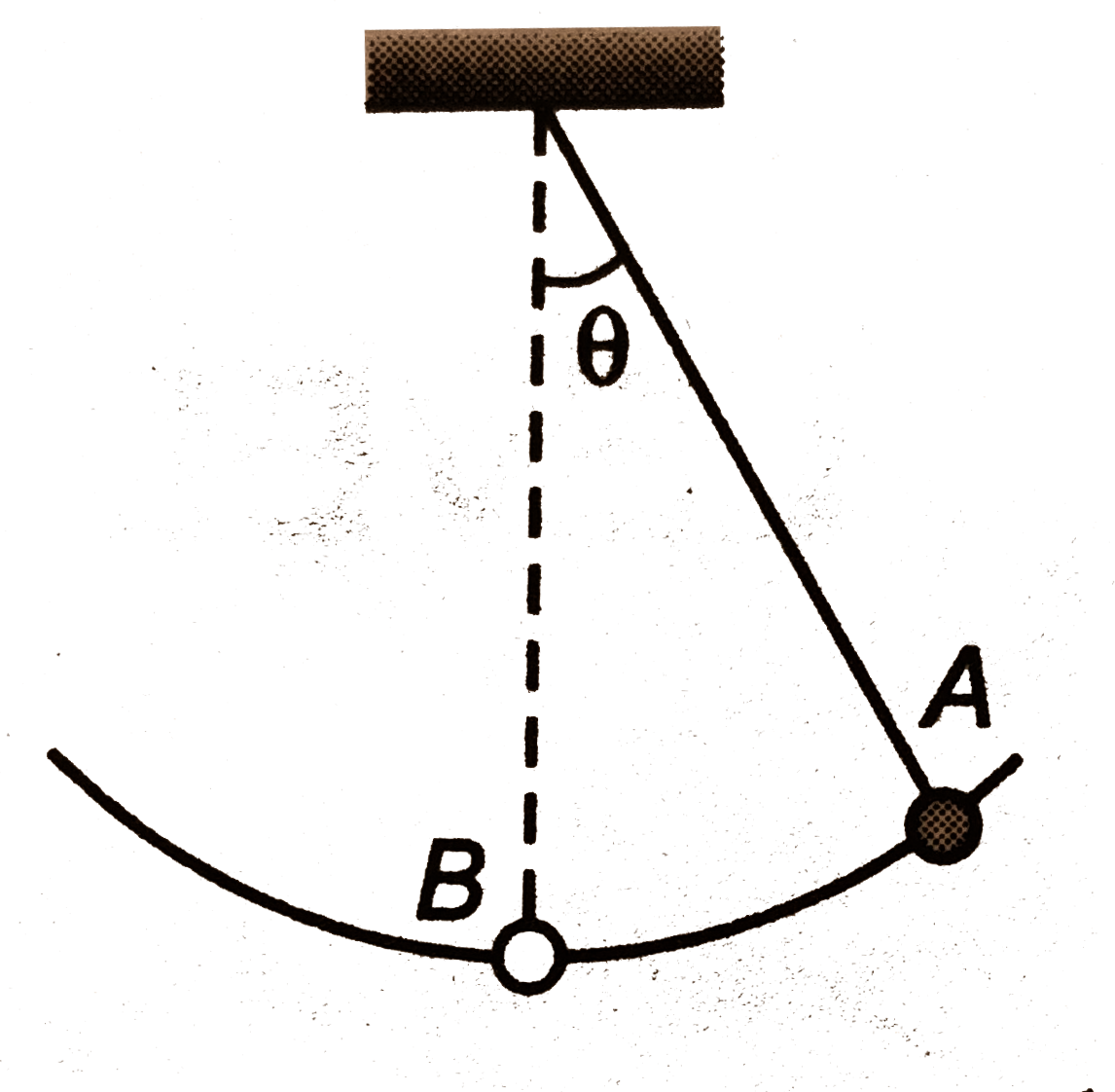
View Solution
Knowledge Check
A stone of mass m tied to the end of a string, is whirled around in a horizontal circle. (Neglect the force due to gravity). The length of the string is reduced gradually keeping the angular momentum of the stone about the centre of the circle constant. Then, the tension in the string is given by T=Arn where A is a constant, r is the instantaneous radius of the circle and n=....
Aa. -3Bb. 3Cc. 2Dd. -4
A massless, inextensible string of length 1 m has a breaking strength of 1 kg wt. A stone of mass 0.2 kg tied to one end of the string is made to move in a vertical circle. Can the stone describe the vertical circle? (g=10ms−2)
View SolutionA particle is fastened at the end of a string and whirled in a vertical circle with the other end of the string being fixed. The motion of the particle is
View SolutionA particle of mass m is attached to one end of a light inextensible string and the other end of the string is fixed in vertical plane as shown. Particle is given a horizontal velocity u=√52gl

The maximum angle made by the string with downward vertical is
View SolutionA stone is fastened to one end of a string and is whirled in a verticla circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.
View SolutionA block of mass m at the end of a string is whirled round in a vertical circle of radius R. The critical speed of the block at top of its swing below which the string would slacken before the block reaches the bottom is?
View SolutionA stone of mass of 1 kg is tied to the end of a string 1 m long. It is whirled in a vertical circle. The velocity of the stone at the bottom of the circle is just sufficient to take it to the top of circle without slackening of the string. What is the tension in the string at the top of the circle? (Take, g =10 ms−2)
View SolutionA stone of mass 0.3 kg tied to the end of a string in a horizontal plane in whirled round in a circle of radius 1 m withp. speed of 40 rev/min. What is the tension in the string ? What is the maximum speed with which the stone can be whirled around if the string can withstand a maximum tension of 200 N ?
View Solution