A small spherical ball is suspended through a string of length l . The whole arrangement is placed in a vehicle which is moving with velocity v . Now, suddenly the vehicle stops and ball starts moving along a circular path. If tension in the string at the highest point is twice the weight of the ball then (assume that the ball completes the vertical circle)
v=√5gl
v=√7gl
velocity of the ball at highest point is √gl
velocity of the ball at highest point is √3gl
The correct Answer is:B, D
To solve the problem step by step, we will analyze the motion of the ball and apply the principles of conservation of energy and centripetal force.
Step 1: Understand the Setup
A small spherical ball is suspended from a string of length l. When the vehicle stops suddenly, the ball starts moving in a vertical circular path.
Step 2: Define Variables
- Let the mass of the ball be m.
- The initial velocity of the ball when the vehicle stops is v.
- The velocity of the ball at the highest point of the circular path is v'.
- The tension in the string at the highest point is given as T=2mg.
Step 3: Apply Conservation of Energy
Using the conservation of energy between the point where the ball starts moving (point A) and the highest point of the circular path (point B):
\(
\frac{1}{2} mv^2 = \frac{1}{2} mv'^2 + mg(2l)
\)
This equation states that the initial kinetic energy of the ball is equal to the sum of its kinetic energy at the highest point and the potential energy gained when it rises to a height of 2l.
Step 4: Simplify the Energy Equation
Rearranging the equation gives:
\(
\frac{1}{2} mv^2 = \frac{1}{2} mv'^2 + 2mgl
\)
Dividing through by m:
\(
\frac{1}{2} v^2 = \frac{1}{2} v'^2 + 2gl
\)
Multiplying through by 2:
\(
v^2 = v'^2 + 4gl \quad \text{(Equation 1)}
\)
Step 5: Analyze Forces at the Highest Point
At the highest point (point B), the forces acting on the ball are the tension in the string and the weight of the ball. The net force provides the centripetal force required for circular motion:
\(
T + mg = \frac{mv'^2}{l}
\)
Substituting the given tension:
\(
2mg + mg = \frac{mv'^2}{l}
\)
This simplifies to:
\(
3mg = \frac{mv'^2}{l}
\)
Dividing through by m:
\(
3g = \frac{v'^2}{l}
\)
Rearranging gives:
\(
v'^2 = 3gl \quad \text{(Equation 2)}
\)
Step 6: Substitute Equation 2 into Equation 1
Now, substitute Equation 2 into Equation 1:
\(
v^2 = 3gl + 4gl
\)
This simplifies to:
\(
v^2 = 7gl
\)
Taking the square root gives:
\(
v = \sqrt{7gl}
\)
Step 7: Find the Velocity at the Highest Point
From Equation 2, we already found:
\(
v' = \sqrt{3gl}
\)
Conclusion
The initial velocity of the ball when the vehicle stops is \( v = \sqrt{7gl} \) and the velocity at the highest point is \( v' = \sqrt{3gl} \).
Final Answers
- The initial velocity \( v = \sqrt{7gl} \)
- The velocity at the highest point \( v' = \sqrt{3gl} \)
A small spherical ball is suspended from a string of length l. When the vehicle stops suddenly, the ball starts moving in a vertical circular path.
- Let the mass of the ball be m.
- The initial velocity of the ball when the vehicle stops is v.
- The velocity of the ball at the highest point of the circular path is v'.
- The tension in the string at the highest point is given as T=2mg.
Using the conservation of energy between the point where the ball starts moving (point A) and the highest point of the circular path (point B):
\frac{1}{2} mv^2 = \frac{1}{2} mv'^2 + mg(2l)
\)
Rearranging the equation gives:
\frac{1}{2} mv^2 = \frac{1}{2} mv'^2 + 2mgl
\)
\frac{1}{2} v^2 = \frac{1}{2} v'^2 + 2gl
\)
v^2 = v'^2 + 4gl \quad \text{(Equation 1)}
\)
At the highest point (point B), the forces acting on the ball are the tension in the string and the weight of the ball. The net force provides the centripetal force required for circular motion:
T + mg = \frac{mv'^2}{l}
\)
2mg + mg = \frac{mv'^2}{l}
\)
3mg = \frac{mv'^2}{l}
\)
3g = \frac{v'^2}{l}
\)
v'^2 = 3gl \quad \text{(Equation 2)}
\)
Now, substitute Equation 2 into Equation 1:
v^2 = 3gl + 4gl
\)
v^2 = 7gl
\)
v = \sqrt{7gl}
\)
From Equation 2, we already found:
v' = \sqrt{3gl}
\)
The initial velocity of the ball when the vehicle stops is \( v = \sqrt{7gl} \) and the velocity at the highest point is \( v' = \sqrt{3gl} \).
- The initial velocity \( v = \sqrt{7gl} \)
- The velocity at the highest point \( v' = \sqrt{3gl} \)
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Level 2 Comprehension Based
Explore 5 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Level 2 Subjective
Explore 13 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Level 2 Single Correct
Explore 18 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
A uniform rod of mass m and length / is hinged at upper end. Rod is free to rotate in vertical plane. A bail of mass m moving horizontally with velocity vo collides at lower end of rod perpendicular to it and sticks to it. The minimum velocity of the ball such that combined system just completes the vertical circle will be
View SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
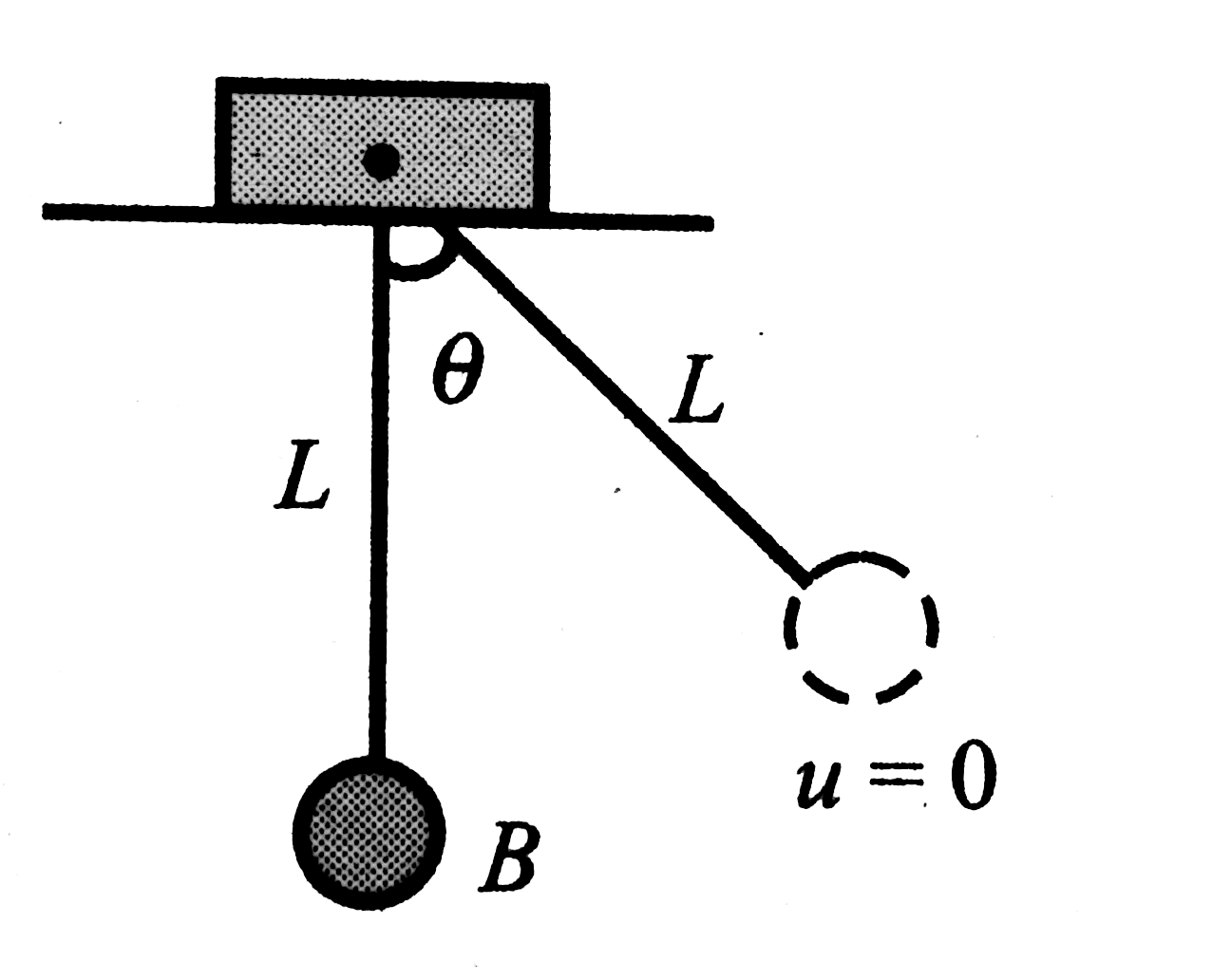
Tension in string when it is vertical, is
View SolutionA ball of mass m is attached to one end of a light rod of length l, the other end of which is hinged. What minimum velocity v should be imparted to the ball downwards, so that it can complete the circle ?

View SolutionA bob is attached to a string of length l whose other end is fixed and is given horizontal velocity at the lowest point of the circle so that the bob moves in a vertical plane. Match the velocity given at the lowest point of circle in column I with tension and velocity at the highest point of the circle corresponding to velocity of column I of column II

View SolutionTwo metallic balls of mass m are suspended by two strings of length L. The distance between upper ends is L. The angle at which the string will be inclined with vertical due to attraction is (m<<M where M is the mass of Earth)
View SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
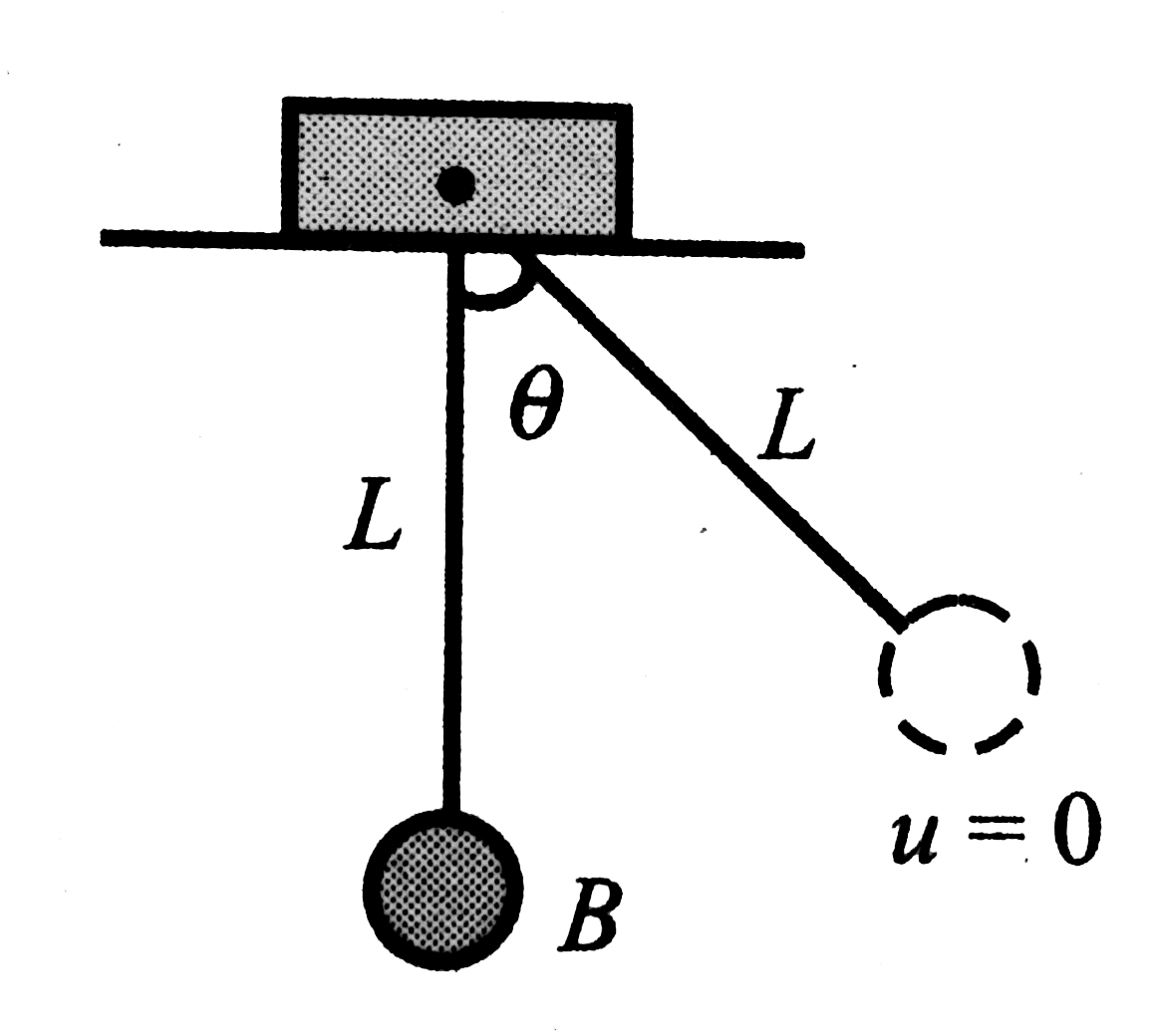 The displacement of centre of mass of A+B system till the string becomes vertical is
The displacement of centre of mass of A+B system till the string becomes vertical is
View SolutionIn all the four situations depicted in Column-I, a ball of mass m is connected to a string. In each case, find the tension in the string and match the appropriate entries in Column-II.
(A)(##VMCPHYXIWORBOK01_C04E03050_Q01##)Conical pendulum(P)T=mgcosθ(B)(##VMCPHYXIWORBOK01_C04E03050_Q02##)Pendulum is swinging. Angular position is the extreme position.T is tension in extreme position(Q)Tcosθ=mg(C)(##VMCPHYXIWORBOK01_C04E03050_Q03##)The car is moving with constant acceleration.The ball is at rest with respect to car(R)Speed of ball with respect to ground is constant(D)(##VMCPHYXIWORBOK01_C04E03050_Q04##)The car is moving with constant velocity. The ball is at rest with respect to car(S)Velocity of ball with respect to ground is changing continuously
View Solutionn elastic balls are placed at rest on a smooth horizontal plane which is circular at the ends with radius r as shown in the figure. The masses of the balls are m, m2, m22, …………….m2n−1 respectively. What is the minimum velocity which should be imparted to the first ball of mass m such that nth ball completes the vertical circle

View Solutionn elastic balls are placed at rest on a smooth horizontal plane which is circular at the ends with radius r as shown in the figure. The masses of the balls are m, m2, m22, …………….m2n−1 respectively. What is the minimum velocity which should be imparted to the first ball of mass m such that nth ball completes the vertical circle

View SolutionA simple pendulum of length l is suspended from the ceilling of a car moving with a speed v on a circular horizontal road of radius r. a. Find the tension in the string when it is at rest with respect to the car. b.Find the time period of small oscillation.
View Solution

