The string of a pendulum is horizontal. The mass of the bob is m. Now the string is released. The tension in the string in the lowest position is -
mg
2 mg
3 mg
4 mg
The correct Answer is:C
To solve the problem of finding the tension in the string of a pendulum at its lowest position after being released from a horizontal position, we can follow these steps:
1. Understand the Setup:
- The pendulum consists of a string of length l with a bob of mass m attached to it.
- The string is initially horizontal and then released.
2. Identify Forces at the Lowest Point:
- At the lowest point (let's call it point B), the forces acting on the bob are:
- The gravitational force mg acting downward.
- The tension T in the string acting upward.
3. Use Conservation of Mechanical Energy:
- Since the pendulum is released from rest, we can use the conservation of mechanical energy to find the speed of the bob at the lowest point.
- At the initial position (point A), the potential energy (PE) is maximum and kinetic energy (KE) is zero:
PEA=mgh=mgL(since height h=L)
- At the lowest point (point B), the potential energy is zero and the kinetic energy is maximum:
PEB=0,KEB=12mv2
4. Set Up the Energy Conservation Equation:
- According to the conservation of energy:
PEA+KEA=PEB+KEB
mgL+0=0+12mv2
- Simplifying gives:
mgL=12mv2
5. Solve for the Speed v:
- Cancel m from both sides (assuming m≠0):
gL=12v2
- Rearranging gives:
v2=2gL
6. Calculate the Tension at the Lowest Point:
- At the lowest point, we can apply Newton's second law:
T−mg=mv2l
- Substitute v2 from the previous step:
T−mg=m(2gL)l
- Rearranging gives:
T=mg+2mgLl
- Since L=l, we have:
T=mg+2mg=3mg
Final Answer:
The tension in the string at the lowest position is T=3mg.
---
- The pendulum consists of a string of length l with a bob of mass m attached to it.
- The string is initially horizontal and then released.
- At the lowest point (let's call it point B), the forces acting on the bob are:
- The gravitational force mg acting downward.
- The tension T in the string acting upward.
- Since the pendulum is released from rest, we can use the conservation of mechanical energy to find the speed of the bob at the lowest point.
- At the initial position (point A), the potential energy (PE) is maximum and kinetic energy (KE) is zero:
PEA=mgh=mgL(since height h=L)
- At the lowest point (point B), the potential energy is zero and the kinetic energy is maximum:
PEB=0,KEB=12mv2
- According to the conservation of energy:
PEA+KEA=PEB+KEB
mgL+0=0+12mv2
- Simplifying gives:
mgL=12mv2
- Cancel m from both sides (assuming m≠0):
gL=12v2
- Rearranging gives:
v2=2gL
- At the lowest point, we can apply Newton's second law:
T−mg=mv2l
- Substitute v2 from the previous step:
T−mg=m(2gL)l
- Rearranging gives:
T=mg+2mgLl
- Since L=l, we have:
T=mg+2mg=3mg
The tension in the string at the lowest position is T=3mg.
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Match the columns
Explore 3 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Medical entrances s gallery
Explore 19 Videos
- CIRCULAR MOTIONBook:DC PANDEY ENGLISHChapter:CIRCULAR MOTIONExercise:Check point
Explore 45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEY ENGLISHChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
The mass of the part of the string below A in figure is m. Find the tension of the string at the lower end and at A.
View SolutionA simple pendulum consists of a 50 cm long string connected to a 100 g ball. The ball is pulled aside so that the string makes an angel of 370 with the vertical and is then released. Find the tension in the string when the bob is at its lowest position.

View SolutionA pendulum bob swings along a circular path on a smooth inclined plane as shown in figure, where m=3kg, l=0.75m, θ=37∘. At the lowest point of the circle the tension in the string is T=274N. Take g=10ms−2.
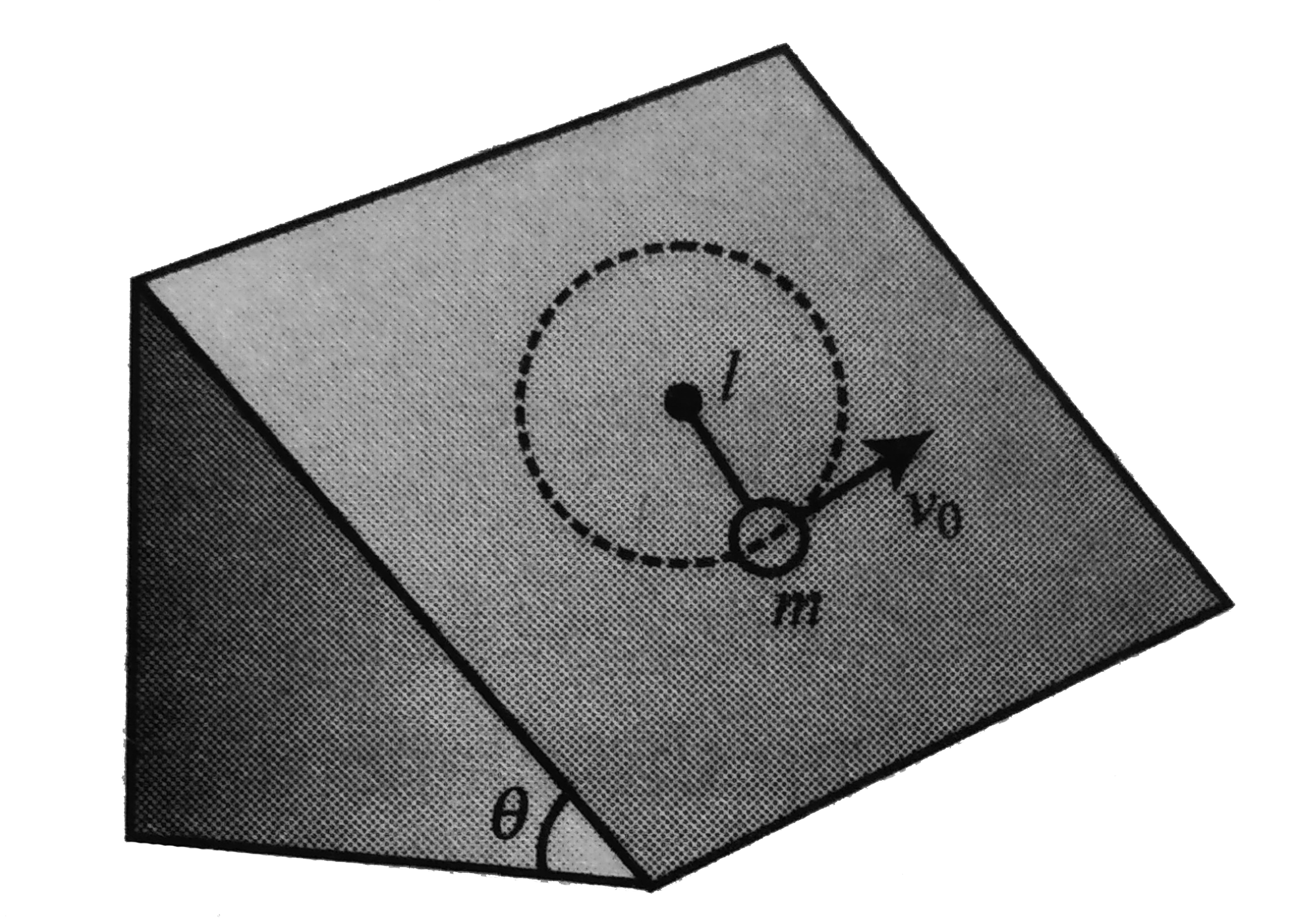
The tension in the string at the highest position is
View SolutionThe block of mass m is at rest. Find the tension in the string A .

View SolutionA simple pendulum of length l and mass m is initially at its lowest position. It is given the minimum horizontal speed necessary after to move in a circular path about the point of suspension. The tension in the string at the lowest positive of the bob is
View SolutionLet θ denote the angular displacement of a simple pendulum oscillating in a vertical plane. If the mass of the bob is m, the tension in the string is mgcosθ
View SolutionA stone is tied to one end of a string and rotated in horizontal circle with a uniform angular velocity. The tension in the string is T, if the length of the string is halved and its angular velocity is doubled , the tension in the string will be
View SolutionSuppose the amplitude of a simple pendulum having a bob of mass m is θ0. Find the tension in the string when the bob is at its extreme position.
View Solutionwhen the bob of a simple pendulum swings, the work done by tension in the string is :
View SolutionThe string of pendulum of length l is displaced through 90∘ from the vertical and released. Then the minimum strength of the string in order to withstand the tension, as the pendulum passes through the mean position is
View Solution