A particle starts travelling on a circle with constant tangential acceleration. The angle between velocity vector and acceleration vector, at the moment when particle completes half the circular track. Is
tan−1(2π)
tan−1(π)
tan−1(3π)
zero
The correct Answer is:A
v=√2ats=√2at(πR)

∴ an=v2R=2πat
or anat=2π⇒tanθ=anat=2π
∴ θ=tan−1(2π)
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns
3 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Check point
45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
Knowledge Check
Velocity vector and acceleration vector in a uniform circular motion are related as
Aboth in the same directionBperpendicular to each otherCboth in opposite directionDnot related to each other
A particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
View SolutionA particle starts from rest with constant acceleration. The ratio of space-average velocity to the time average velocity is :-
View SolutionA disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity ad acceleration vectors of point P is

View SolutionA disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity and acceleration vectors of point P is
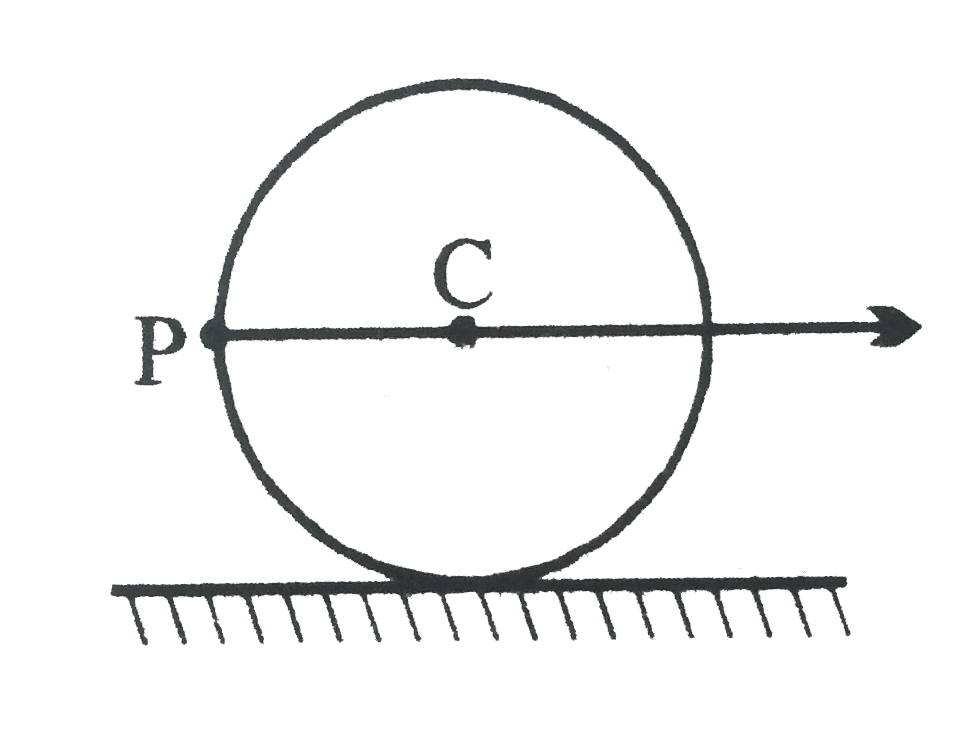 .
.
View SolutionIf a particle is moving on a circular path with constant speed, then the angle between the direction of acceleration and its position vector w.r.t. centre of circle will be
View SolutionAssertion:- A particle is moving in a circle with constant tangential acceleration such that its speed v is increasing. Angle made by resultant acceleration of the particle with tangential acceleration increases with time.
Reason:- Tangential acceleration =∣∣∣d→vdt∣∣∣ and centripetal acceleration =v2R
View SolutionA particle starts moving along a circle of radius (20/π)m with constant tangential acceleration. If the velocity of the parthcle is 50m/s at the end of the second revolution after motion has began, the tangential acceleration in m/s2 is :
View Solution
