The sphere at A is given a downward velocity v0 of magnitude 5m/s and swings in a vertical plane at the end of a rope of length l=2m attached to a support at O . Determine the angle θ at which the rope will breack, knowing that it can withstant a maximum tension equal to twich the weight of the sphere.
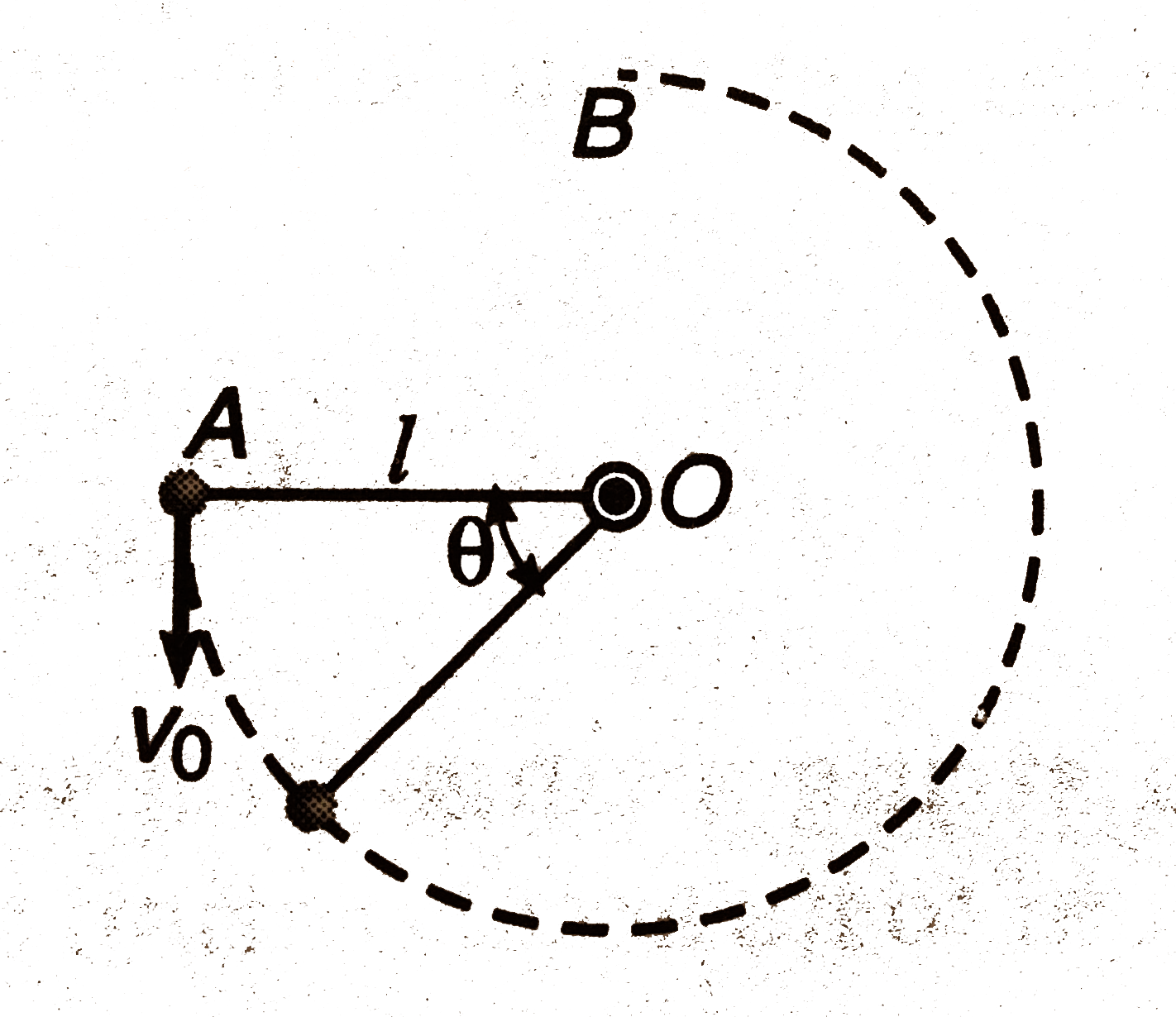
The correct Answer is:A, D
v2=v20+2gh=v20+2gRsinθ
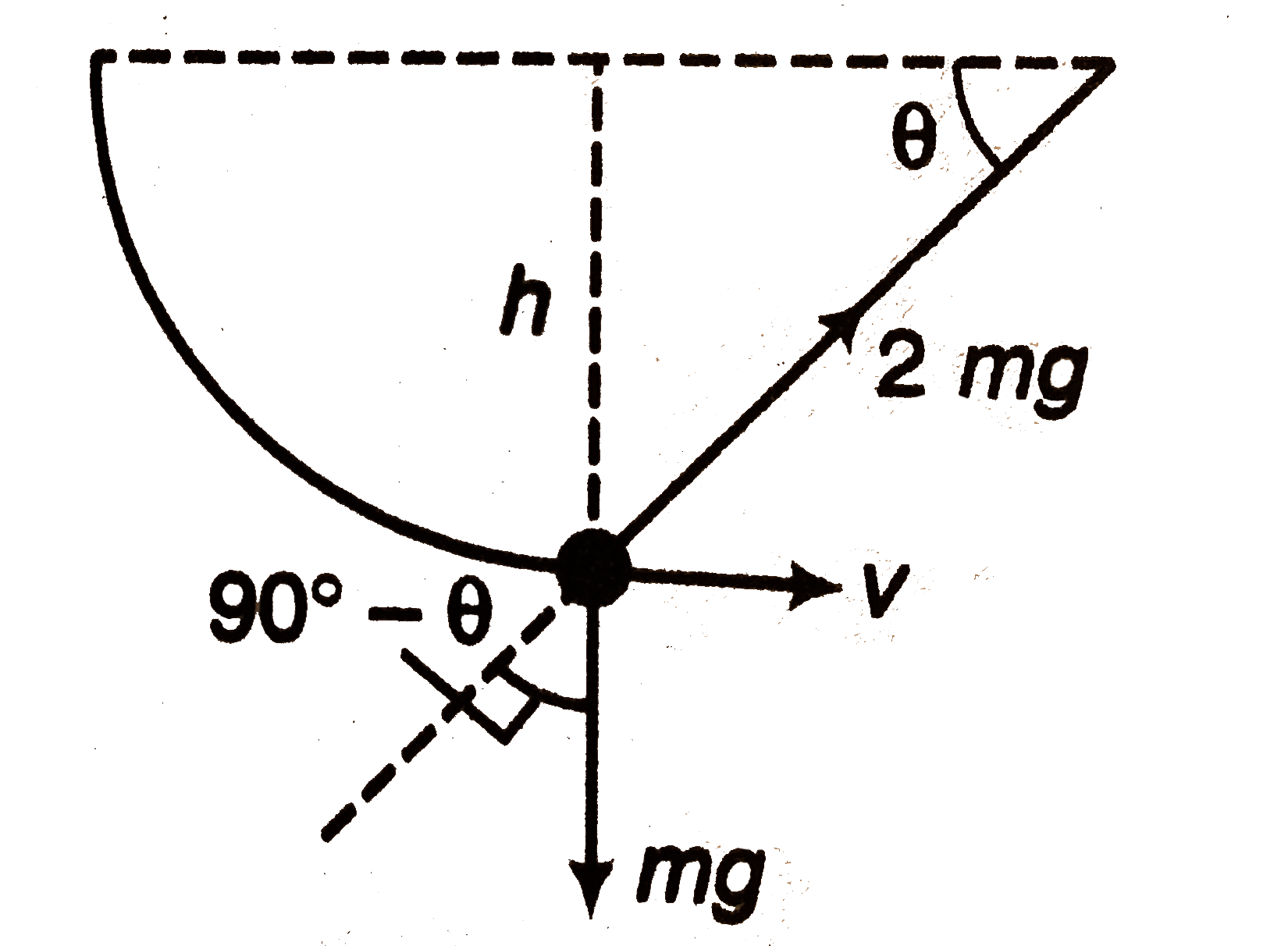
=(5)2+2×10×2sinθ
=(25+40sinθ)
Now, 2mg−mgsinθ=mv2R
or 2g−gsinθ=v2R
or 2×10−10sinθ=25+40sinθ=25+40sinθ2
Solving this equation we get,
θ=sin−1(14)
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Single Correct
18 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 More Than One Correct
5 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 1 Objective
14 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
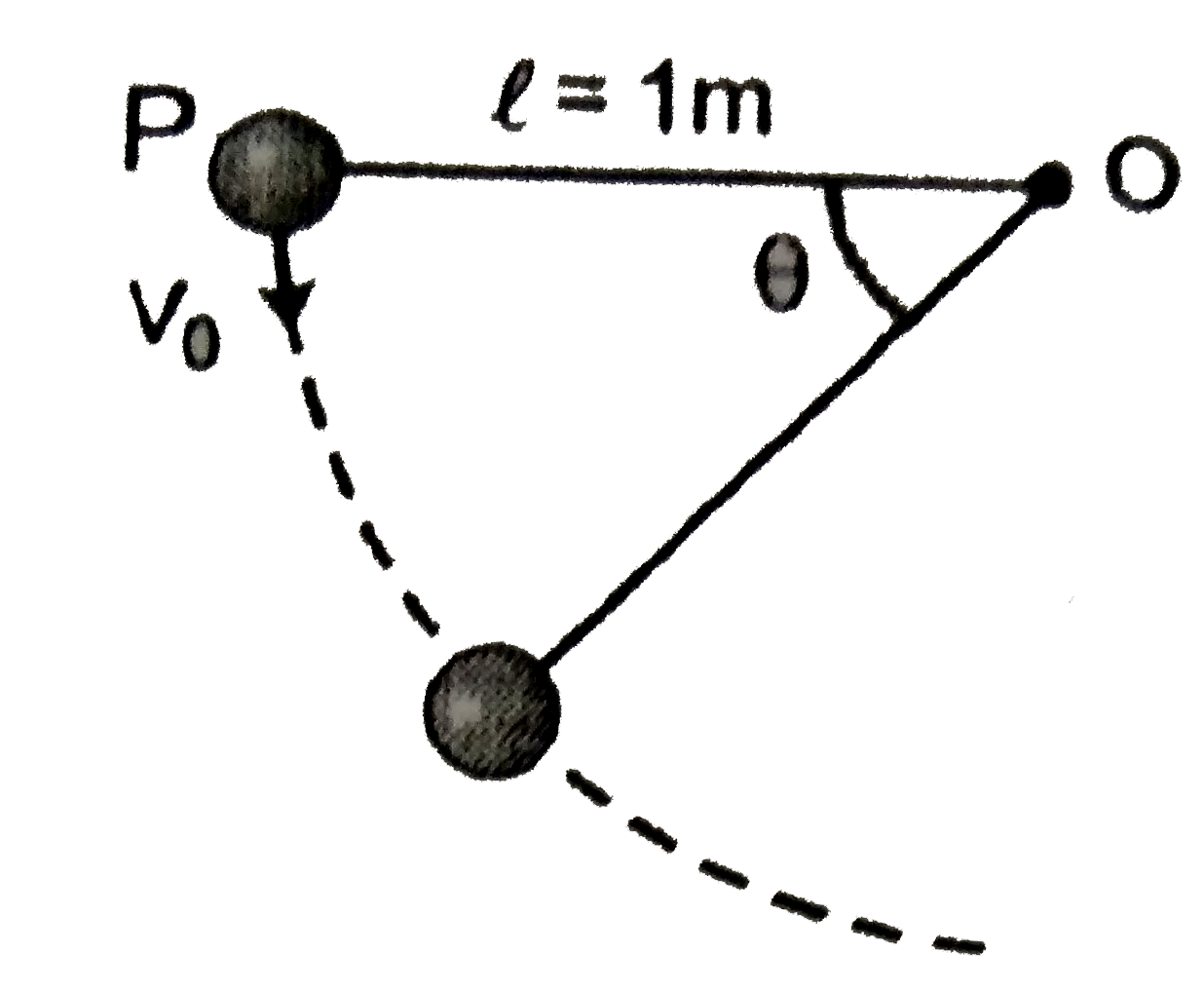
The sphere at P is given a downward velocity v0 and swings in a vertical plane at the end of a rope of l=1m attached to a support at O. The rope breaks at angle 30∘ from horizontal , knowing that it can withstand a maximum tension equal to three times the weight of the sphere. Then the value of v0 will be :
(g=π2m/s2)
View SolutionA small sphere is given vertical velocity of magnitude v0=5ms−1 and it swings in a vertical plane about the end of a massless string. The angle θ with the vertical at which string will break, knowing that it can withstand a maximum tension equal to twice the weight of the sphere, is
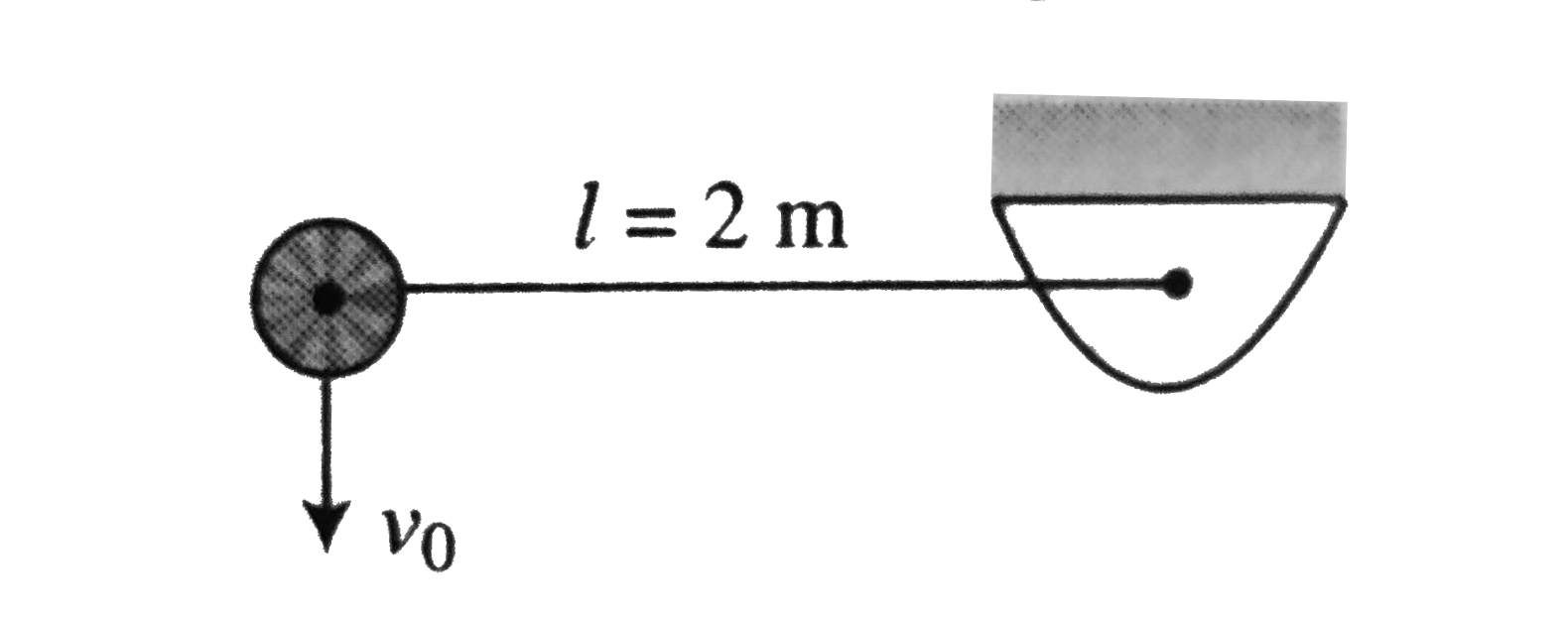
View SolutionA stone of mass 0.5 kg is attached to a string of length 2 m and is whirled in a horizontal circle. If the string can with stand a tension of 9N, the maximum velocity with which the stone can be whirled is:
View SolutionA ball of mass m is attached to one end of a light rod of length l, the other end of which is hinged. What minimum velocity v should be imparted to the ball downwards, so that it can complete the circle ?

View SolutionA sphere of radius 0.1m and mass 8πkg is attached to the lower end of a steel wire of length 5.0m and diameter 10−3. The wire is suspended from 5.22m high ceiling of a room . When the sphere is made to swing as a simple pendulum, it just grazes the floor at its lowest point. Calculate the velocity of the sphere at the lowest position . Young's modulus of steel is (1.994×1011N/m2).
View SolutionA sphere of mass 20 kg is suspended by a metal wire of unstretched length 4 m and diameter 1 mm. When in equilibrium there is a clear gap of 2 mm between the sphere and the floor. The sphere is gently pushed aside so that the wire makes an angle θ with the vertical and is released. Find the maximum value of θ so that the sphere does not rub the floor. young's modulus of the metal of the wire is 2.0×1011Nm−2. Make appropriate approximation.
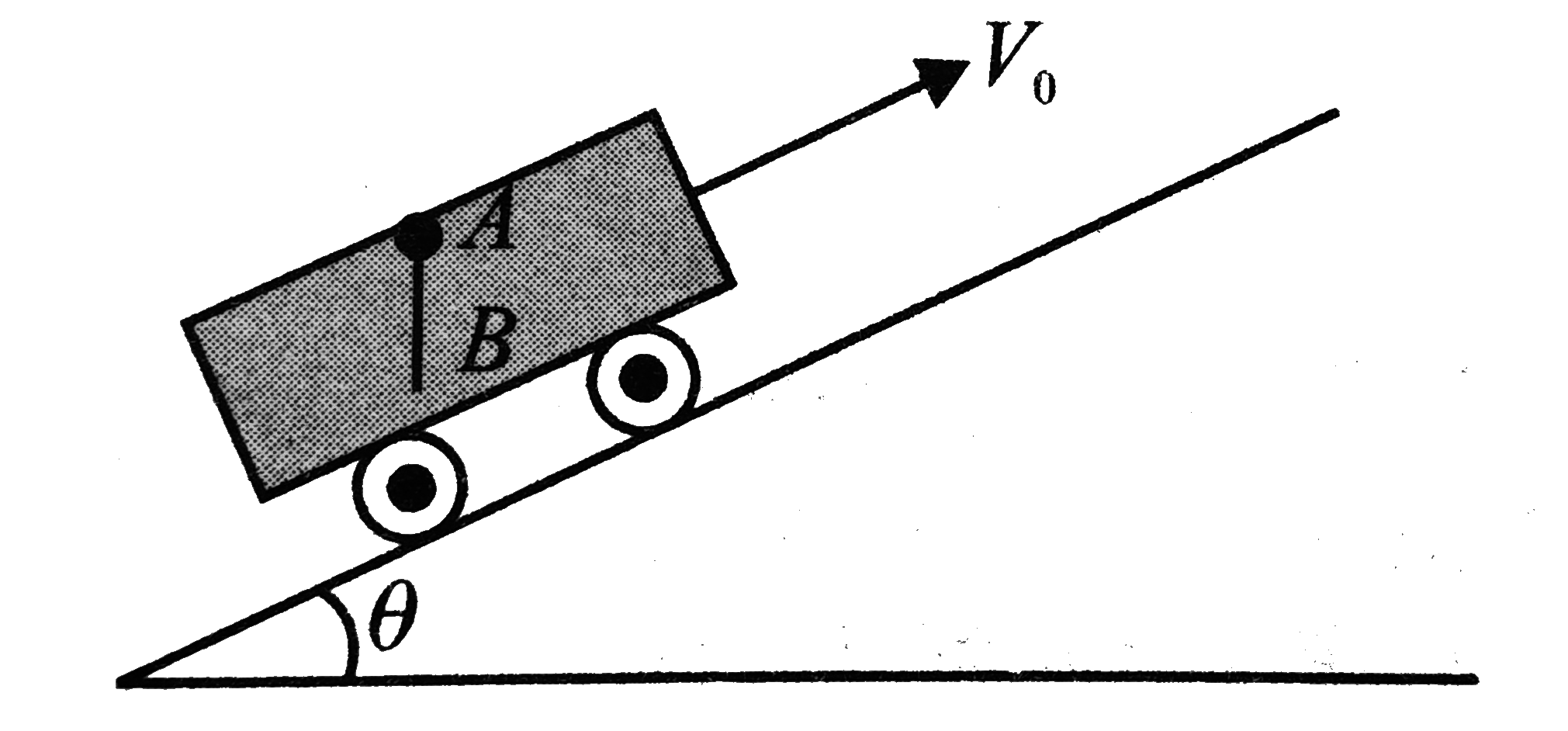
View SolutionA uniform rod AB of length l and mass m hangs from point A in a car moving with velocity v0 on an inclined plane as shown in Fig. The rod can rotate in vertical plane about the axis at point A. if the car suddenly stops, the angular speed with which the rod starts rotating is
View SolutionA smooth rope of mas m and length L lies in a heap on a smooth horizontal floor, with one end attached to a block of mass M. The block is given a sudden kick and instantaneously acquires a horizontal velocity of magnitude V0 as shown in figure 1. As the block moves to right pulling the rope from heap, the rope being smooth, the heap remains at rest. At the instant block is at a distance x from point P as shown in figure −2(P is a point on the rope which has just started to move at the given instant ), choose correct options for next three question.

The speed of block of mass M is
View SolutionA mass m attached to spring of natural length l0 and spring constant k. One end of string is attached to centre of disc in horizontal plane which is being rotated by constant angular speed ω. Find extension per unit length in spring (given k>>mω2 ) :
View SolutionThe small particle of mass m is given an initial high velocity in the horizontal plane and winds its cord around the fixed vertical shaft of radius 1m. All motion occurs essentially in the horizontal plane. If the angular velocity of the cord is 0.8 rad/s when the distance from the particle to the tangency point is 5m, determine the angular velocity ω (in rad//s) of the cord after it has turned through an angle 1 rad.
View Solution
