A small sphere is given vertical velocity of magnitude v0=5ms−1 and it swings in a vertical plane about the end of a massless string. The angle θ with the vertical at which string will break, knowing that it can withstand a maximum tension equal to twice the weight of the sphere, is
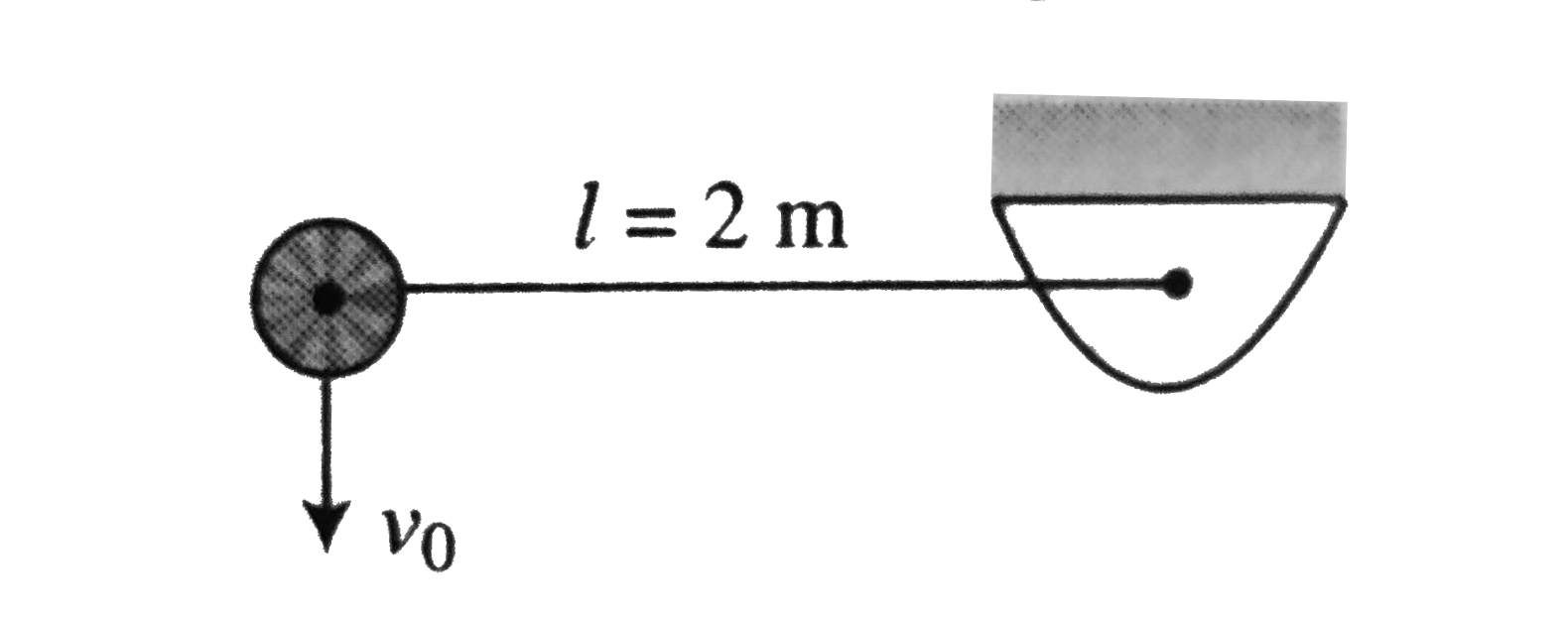
(a) cos−123
(b) cos−1(14)
(c) 60∘
(d) 30∘
The correct Answer is:B
v2=v20+2glcosθ
T=mgcosθ+mv2l
Given T=2mg
2mg=mgcosθ+ml(v20+2glcosθ)mgcosθ
⇒cosθ=14

Topper's Solved these Questions
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Multiple Correct
Explore 25 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Linked Comprehension
Explore 55 Videos
- WORK, POWER & ENERGYBook:CENGAGE PHYSICS ENGLISHChapter:WORK, POWER & ENERGYExercise:Subjective
Explore 23 Videos
- VECTORSBook:CENGAGE PHYSICS ENGLISHChapter:VECTORSExercise:Exercise Multiple Correct
Explore 5 Videos
Similar Questions
The sphere at A is given a downward velocity v0 of magnitude 5m/s and swings in a vertical plane at the end of a rope of length l=2m attached to a support at O . Determine the angle θ at which the rope will breack, knowing that it can withstant a maximum tension equal to twich the weight of the sphere.
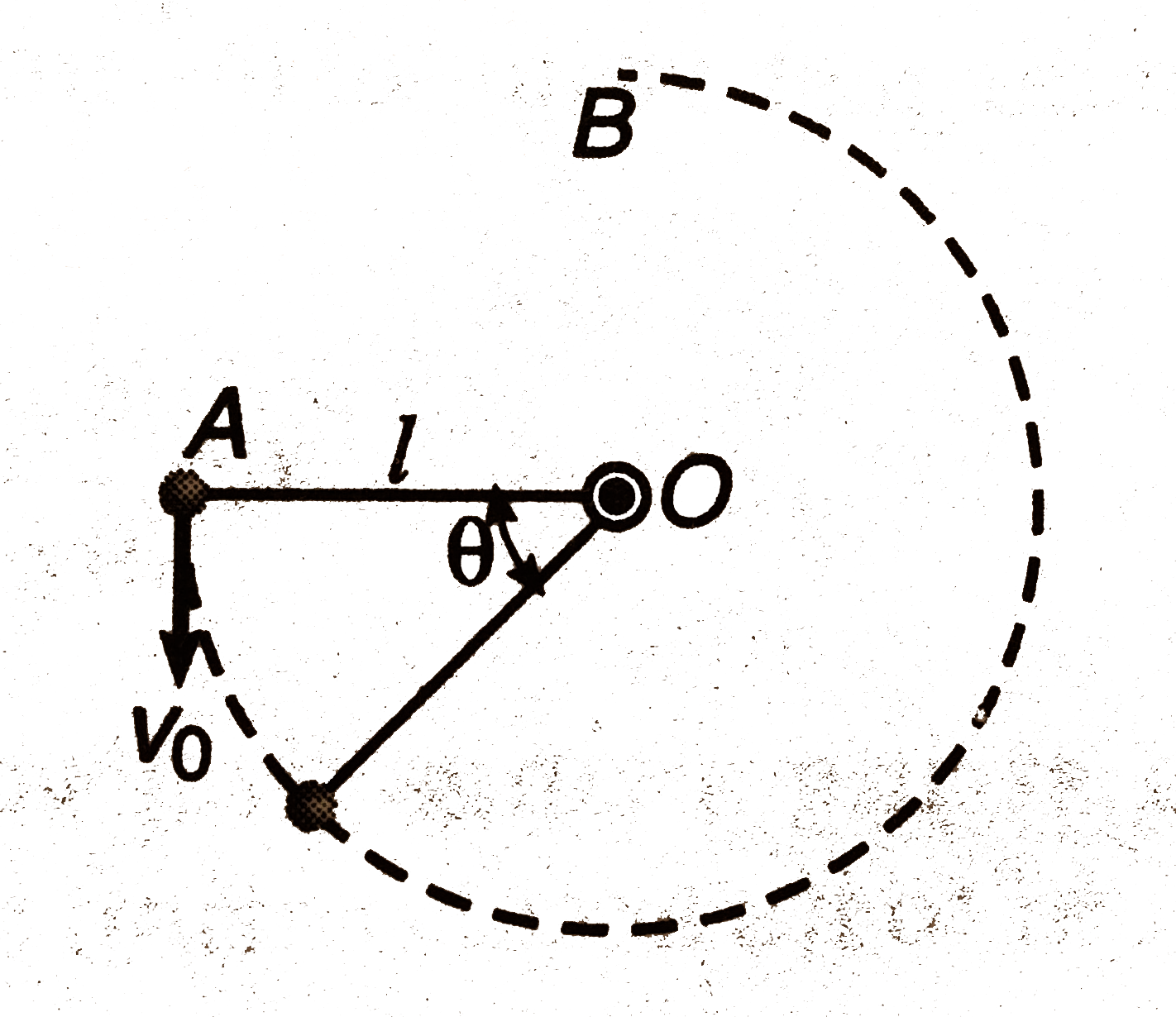
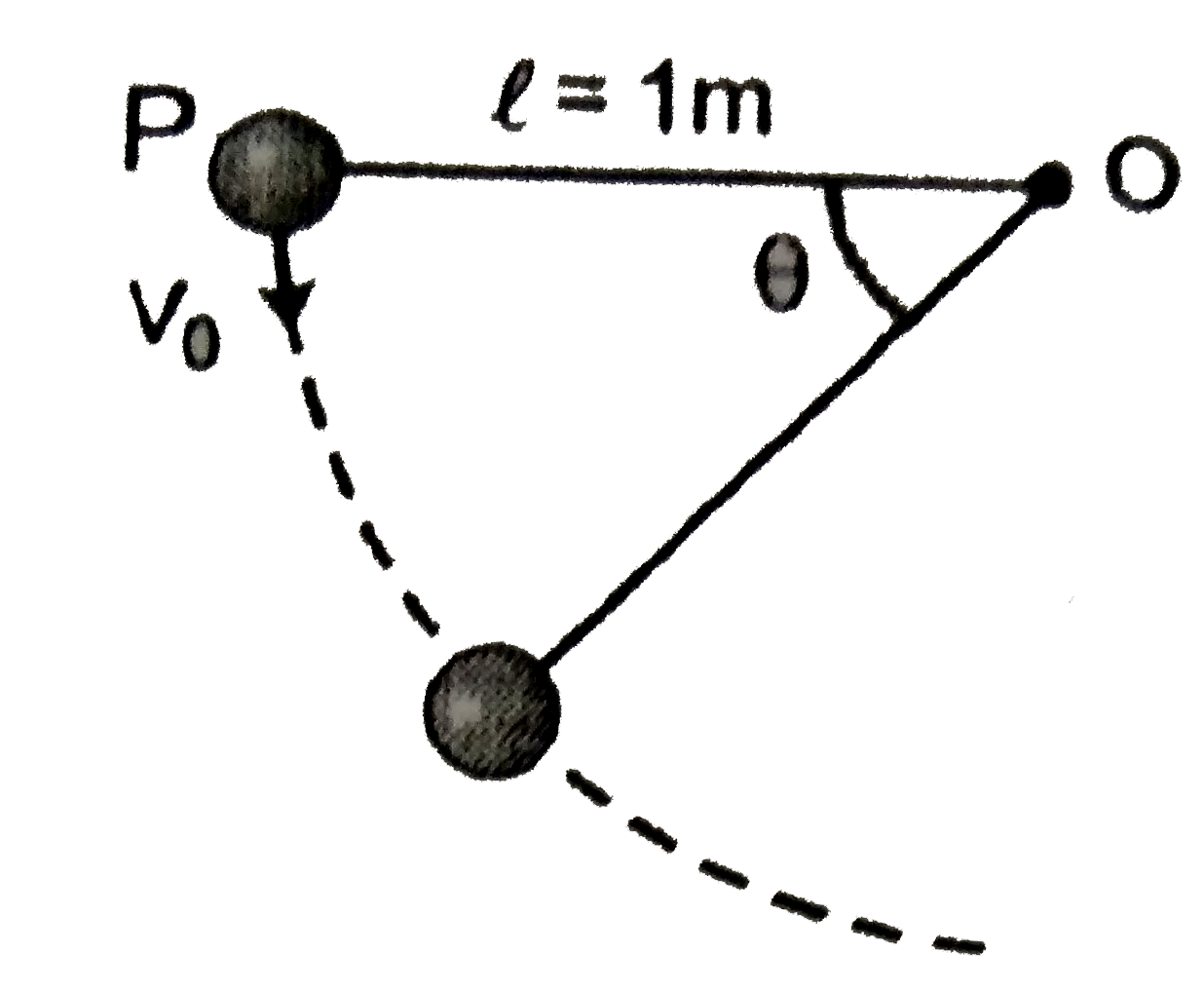
View SolutionThe sphere at P is given a downward velocity v0 and swings in a vertical plane at the end of a rope of l=1m attached to a support at O. The rope breaks at angle 30∘ from horizontal , knowing that it can withstand a maximum tension equal to three times the weight of the sphere. Then the value of v0 will be :
(g=π2m/s2)
View SolutionA simple pendulum has a bob of mass m and swings with an angular amplitude ϕ. The tension in thread is T. At a certain time the string makes an angle θ with the vertical (θ≤ϕ)
View SolutionA particle of mass 200 g , is whirled into a vertical circle of radius 80 cm uisig a massless string The speed of the particle when the string makes an angle of 60∘ with the vertical line is 1.5ms−1. The tension in the string at this position is
View SolutionA solid spherical ball of radius 59m is connected to a point A on the wall with the help of a string which makes an angle θ=45∘ with the vertical. The sphere can rotate freely about its central axis and it is set into rotational motion against the vertical face of the wall with an angular velocity face of the wall with an angular velocity 100 rad s−1. In how much time (in s) will it come to rest ? [μ=0.1]
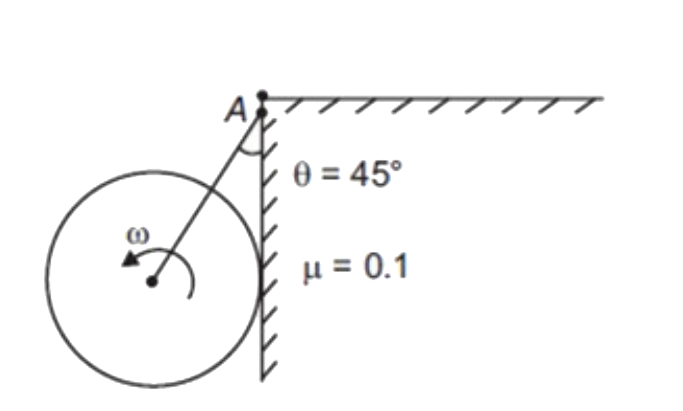
View SolutionA pendulum consists of a small mass m at the end of a string of length L. The pendulum is pulled aside making an angle θ with the vertical and released. Taking the suspension point as the axis, at the instant of release
View SolutionA simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
View SolutionA stone of of mass 0.25 kg tied to the end of a string is whirled round in a circle of radius 1.5 m with a speed of 40rev/min in a horizontal plane What is the tension in the string ? What is the maximum speed with which the stone can be whirled around If the string can withstand a maximum tension of 200 N ?
View SolutionA simple pendulum suspended from the roof off a lift oscillates with frequency υ when the lift is at rest. If the lift falls freely under gravity, its frequency of oscillation becomes
View SolutionA particle tide to the end of a string oscillates along a circular arc in a vertical plane. The other end of the string is fixed at the center of the circle. If the string has a breaking strength of twice the weight of the particles,
a. find the maximum distance that the particle can cover in one cycle of oscillation. The length of the string is 50cm.
b. Find the tension in the extreme position.
c. Find the acceleration of the particle at bottom and extreme position.
View Solution