An infinite ladder network is constructed with 1Ωand 2Ω resistors as shown. Find the equivalent resistance points A and B. 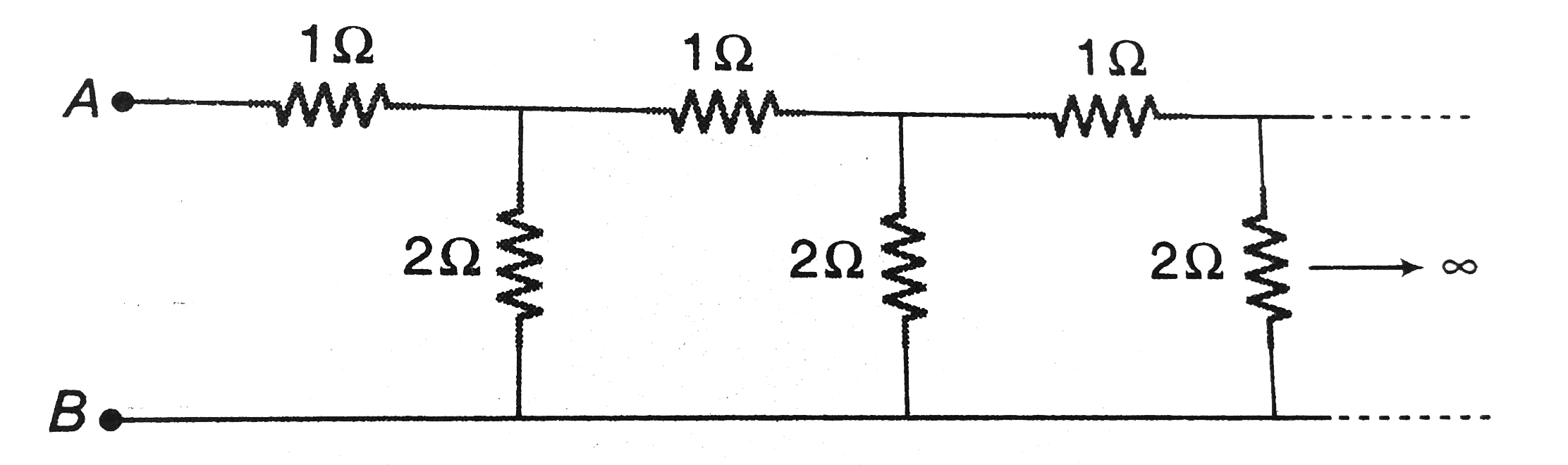
1Ω
2Ω
3Ω
4Ω
The correct Answer is:B
The equivalent circuit is
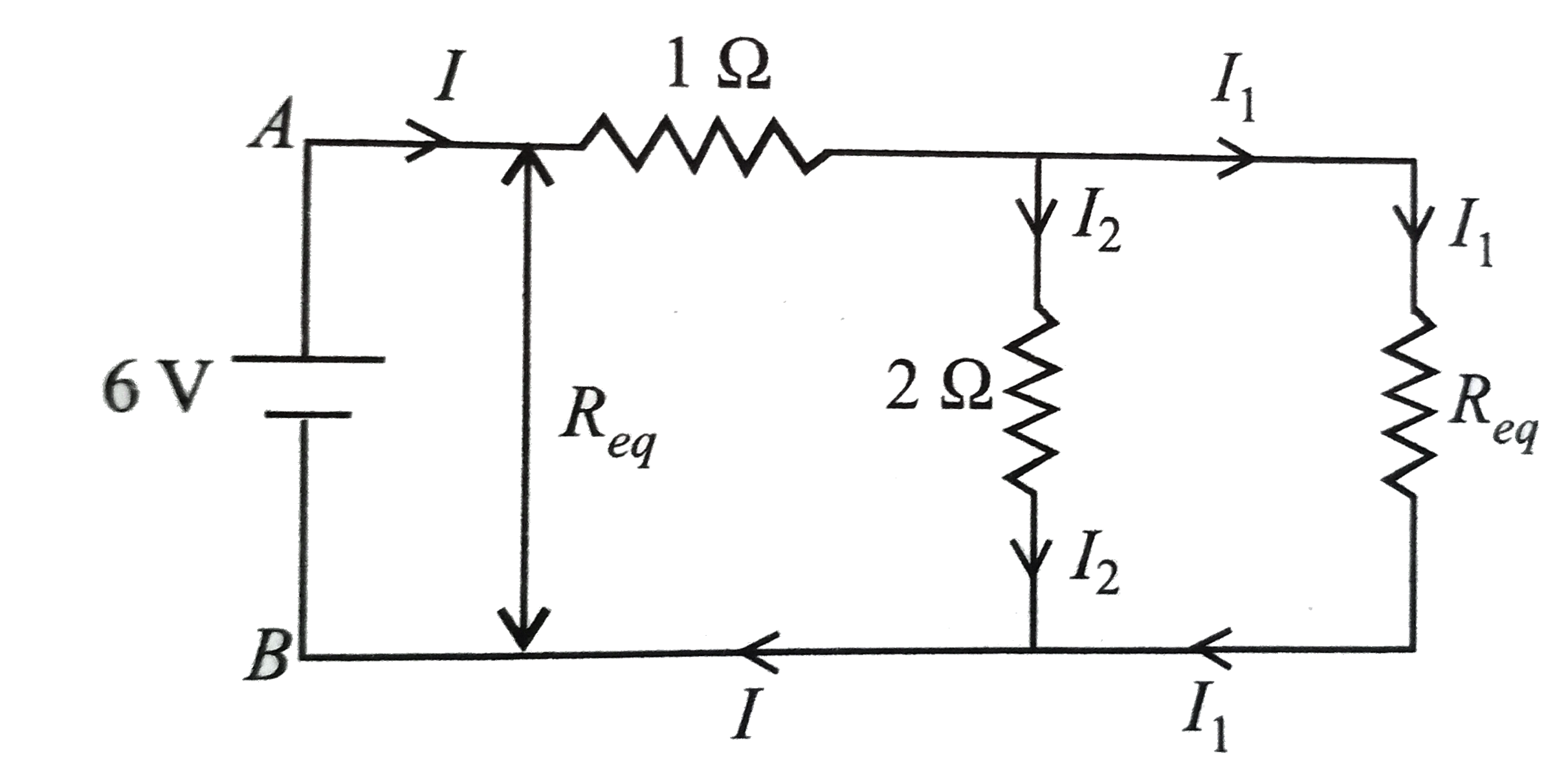
Req=2×Req(2+Req)=2+3Req2+Reqi.e.R2eq−Req−1=0⇒Req=12[1±√1+8=2Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:NCERT FINGERTPS ENGLISHChapter:CURRENT ELECTRICITYExercise:CELLS, EMF, INTERNAL RESISTANCE
Explore 6 Videos
- CURRENT ELECTRICITYBook:NCERT FINGERTPS ENGLISHChapter:CURRENT ELECTRICITYExercise:KIRCHOFF S LAW
Explore 14 Videos
- CURRENT ELECTRICITYBook:NCERT FINGERTPS ENGLISHChapter:CURRENT ELECTRICITYExercise:ELECTRICAL ENERGY, POWER
Explore 8 Videos
- COMMUNITCATION SYSTEMSBook:NCERT FINGERTPS ENGLISHChapter:COMMUNITCATION SYSTEMSExercise:Assertion And Reason
Explore 30 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:NCERT FINGERTPS ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
An infinite ladder network of resistances is constructed with 1Ωand2Ω resistances as shown

View SolutionAn infinite ladder is constructed with 1(Ω)and 2(Ω)resistor as shown in figure.(a)Find the effective resistance between the point A and B. (b) Find the current that passes through the (2Ω) resistor nearest to the battery.

View SolutionIn the network shown, the equivalent resistance between A and B is

View SolutionFor the combination of resistors shown in Fig. find the equivalent resistance between the points
A and B

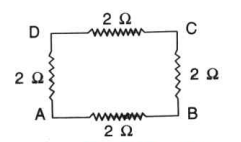
View SolutionIn the network shown in Fig., calculate the equivalent resistance between the points
A and B,
View SolutionFind in the given network of resistors, the equivalent resistance between the points A and B

View SolutionIn the network of resistors shown in the adjoining figure, the equivalent resistance between A and B is

View SolutionEach resistance is of 1Ω in the circuit diagram shown in figure. Find out equivalent resistance between A and B.
View SolutionFind the equivalent resistance of the network shown in figure
View SolutionFor infinite ladder network containing identical resistance of RΩ each, are combined as shown in figure. The equivalent resistance between A and B is RAB and between A and C is RAC. Then the value RABRAC is :

View Solution

