The equivalent resistance of series combination of four equal resistors is S. If they are joined in parallel, the total resistance is P. The relation between S and P is given by S = nP. Then the minimum possible value of n is
12
14
16
10
The correct Answer is:C
To solve the problem, we need to find the minimum possible value of n in the relation S=nP, where S is the equivalent resistance of four equal resistors in series and P is the equivalent resistance of the same resistors in parallel.
1. Define the Resistance of Each Resistor:
Let the resistance of each of the four equal resistors be R.
2. Calculate the Equivalent Resistance in Series:
When resistors are connected in series, the total resistance S is given by:
S=R1+R2+R3+R4=R+R+R+R=4R
3. Calculate the Equivalent Resistance in Parallel:
When the same resistors are connected in parallel, the total resistance P is given by:
1P=1R1+1R2+1R3+1R4=1R+1R+1R+1R=4R
Therefore, rearranging gives:
P=R4
4. Express R in Terms of S and P:
From the series resistance, we have:
R=S4(Equation 1)
From the parallel resistance, we have:
R=4P(Equation 2)
5. Equate the Two Expressions for R:
Set Equation 1 equal to Equation 2:
S4=4P
6. Solve for S:
Multiply both sides by 4:
S=16P
7. Relate S and P:
From the relation S=nP, we can substitute S:
16P=nP
8. Divide Both Sides by P (assuming P≠0):
n=16
Conclusion:
The minimum possible value of n is 16.
Let the resistance of each of the four equal resistors be R.
When resistors are connected in series, the total resistance S is given by:
S=R1+R2+R3+R4=R+R+R+R=4R
When the same resistors are connected in parallel, the total resistance P is given by:
1P=1R1+1R2+1R3+1R4=1R+1R+1R+1R=4R
Therefore, rearranging gives:
P=R4
From the series resistance, we have:
R=S4(Equation 1)
From the parallel resistance, we have:
R=4P(Equation 2)
Set Equation 1 equal to Equation 2:
S4=4P
Multiply both sides by 4:
S=16P
From the relation S=nP, we can substitute S:
16P=nP
n=16
The minimum possible value of n is 16.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:NCERT FINGERTPS ENGLISHChapter:CURRENT ELECTRICITYExercise:CELLS, EMF, INTERNAL RESISTANCE
Explore 6 Videos
- CURRENT ELECTRICITYBook:NCERT FINGERTPS ENGLISHChapter:CURRENT ELECTRICITYExercise:KIRCHOFF S LAW
Explore 14 Videos
- CURRENT ELECTRICITYBook:NCERT FINGERTPS ENGLISHChapter:CURRENT ELECTRICITYExercise:ELECTRICAL ENERGY, POWER
Explore 8 Videos
- COMMUNITCATION SYSTEMSBook:NCERT FINGERTPS ENGLISHChapter:COMMUNITCATION SYSTEMSExercise:Assertion And Reason
Explore 30 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:NCERT FINGERTPS ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
The resistance of the series combination of two resistances is S. When they are joined in parallel the total resistance is P. If S= nP then the minimum possible value of n is
View SolutionThe resistance of the series combination of two resistances is S. When they are joined in parallel the total resistance is P. If S= nP then the minimum possible value of n is
View Solution
Knowledge Check
A wire of resistance .R. is cut into .n. equal parts. These parts are then connected in parallel with each other. The equivalent resistance of the combination is :
AnRBR/nCn/R2DR/n2
The resistance of a series combination of the resistance is S. when they are joined in parallel equvalent resistance is P. Find the value of (S2P)
View SolutionA wire of resistance R is cut into ‘ n ’ equal parts. These parts are then connected in parallel. The equivalent resistance of the combination will be
View SolutionA uniform wire with a resistance of 27 Ω is divided into three equal pieces and then they are joined in parallel. Find the equivalent resistance of the parallel combination
View SolutionThe equivalent resistance between the terminal point P and Q is 4Ω in the given circuit, then find out the resistance of R in ohms
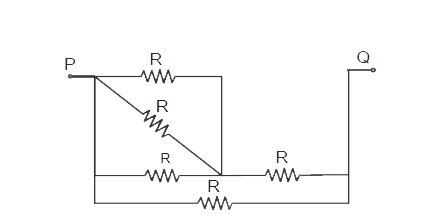
View SolutionSix equal resistance,eacch of resistance R are connected as shown in the figure.Equivalent resistance between P and Q is
_PHY_E05_276_Q01.png)
View SolutionA 5Ω resistor is connected in series with a parallel combination of n resistors of 6Ω each. The equivalent resistance is 7Ω. Find n
View SolutionA combination consists of three resistors in series. Four similar sets are connected in parallel. If the resistance of each resistor is 2 Ω, find the resistance of the combination.
View Solution