n resistors each of resistance R first combine to give maximum effective resistgance and then combine to give minimum. The ratio of the maximum resistance is
n
n2
n2−1
n3
The correct Answer is:B
To solve the problem, we need to find the ratio of the maximum effective resistance to the minimum effective resistance when combining n resistors, each of resistance R.
1. Understanding Series and Parallel Combinations:
- When resistors are combined in series, the effective resistance (R_max) is the sum of the individual resistances.
- When resistors are combined in parallel, the effective resistance (R_min) is given by the reciprocal of the sum of the reciprocals of the individual resistances.
2. Calculating Maximum Resistance:
- For n resistors connected in series:
Rmax=R+R+R+…+R(n times)=nR
3. Calculating Minimum Resistance:
- For n resistors connected in parallel:
1Rmin=1R+1R+1R+…+1R(n times)=nR
- Therefore, the effective resistance is:
Rmin=Rn
4. Finding the Ratio of Maximum to Minimum Resistance:
- Now, we need to find the ratio of maximum resistance to minimum resistance:
Ratio=RmaxRmin=nRRn
- Simplifying this expression:
Ratio=nR⋅nR=n2
5. Final Answer:
- The ratio of the maximum effective resistance to the minimum effective resistance is:
Ratio=n2
- When resistors are combined in series, the effective resistance (R_max) is the sum of the individual resistances.
- When resistors are combined in parallel, the effective resistance (R_min) is given by the reciprocal of the sum of the reciprocals of the individual resistances.
- For n resistors connected in series:
Rmax=R+R+R+…+R(n times)=nR
- For n resistors connected in parallel:
1Rmin=1R+1R+1R+…+1R(n times)=nR
- Therefore, the effective resistance is:
Rmin=Rn
- Now, we need to find the ratio of maximum resistance to minimum resistance:
Ratio=RmaxRmin=nRRn
- Simplifying this expression:
Ratio=nR⋅nR=n2
- The ratio of the maximum effective resistance to the minimum effective resistance is:
Ratio=n2
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:NCERT FINGERTPS ENGLISHChapter:CURRENT ELECTRICITYExercise:CELLS, EMF, INTERNAL RESISTANCE
Explore 6 Videos
- CURRENT ELECTRICITYBook:NCERT FINGERTPS ENGLISHChapter:CURRENT ELECTRICITYExercise:KIRCHOFF S LAW
Explore 14 Videos
- CURRENT ELECTRICITYBook:NCERT FINGERTPS ENGLISHChapter:CURRENT ELECTRICITYExercise:ELECTRICAL ENERGY, POWER
Explore 8 Videos
- COMMUNITCATION SYSTEMSBook:NCERT FINGERTPS ENGLISHChapter:COMMUNITCATION SYSTEMSExercise:Assertion And Reason
Explore 30 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:NCERT FINGERTPS ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
(a) Given n resistors each of resistance R. How will you combine them to get the (i) maximum (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
(b) Given the resistances of 1Ω,2Ω,3Ω, how will you combine them to get an equivalent resistance of (i) (11/3)Ω (ii) (11/5)Ω (iii) 6Ω (iv) (6/11)Ω ?
(c) Determine the equivalent resistance of networks shown in Figure.
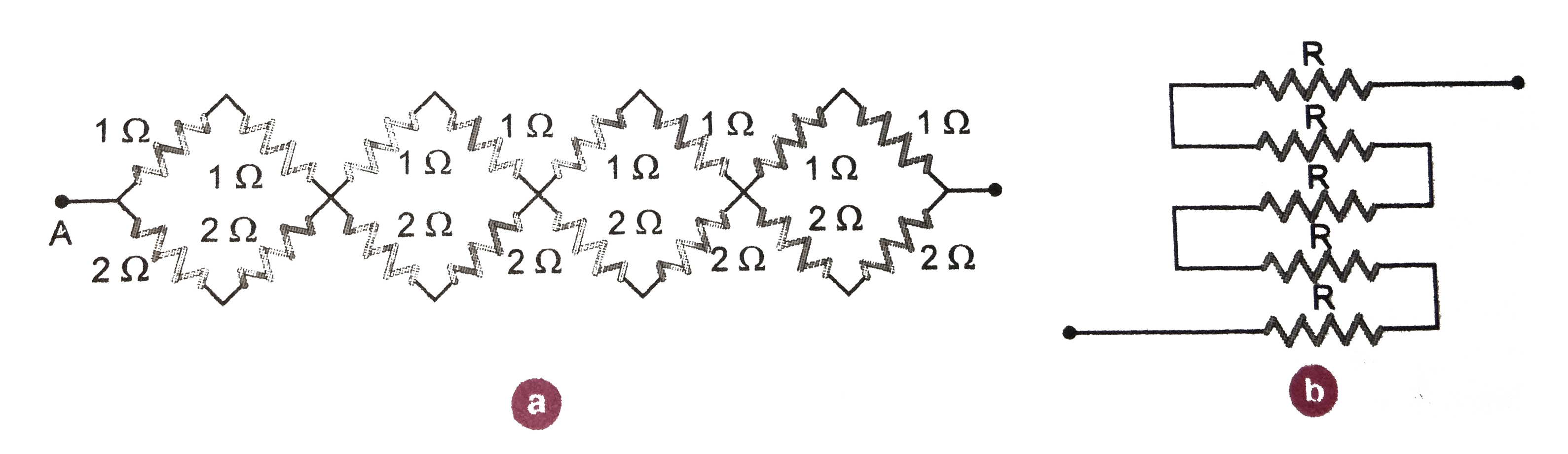
View SolutionFour resistors each of resistance 2 Ω are connected in parallel. What is the effective resistance ?
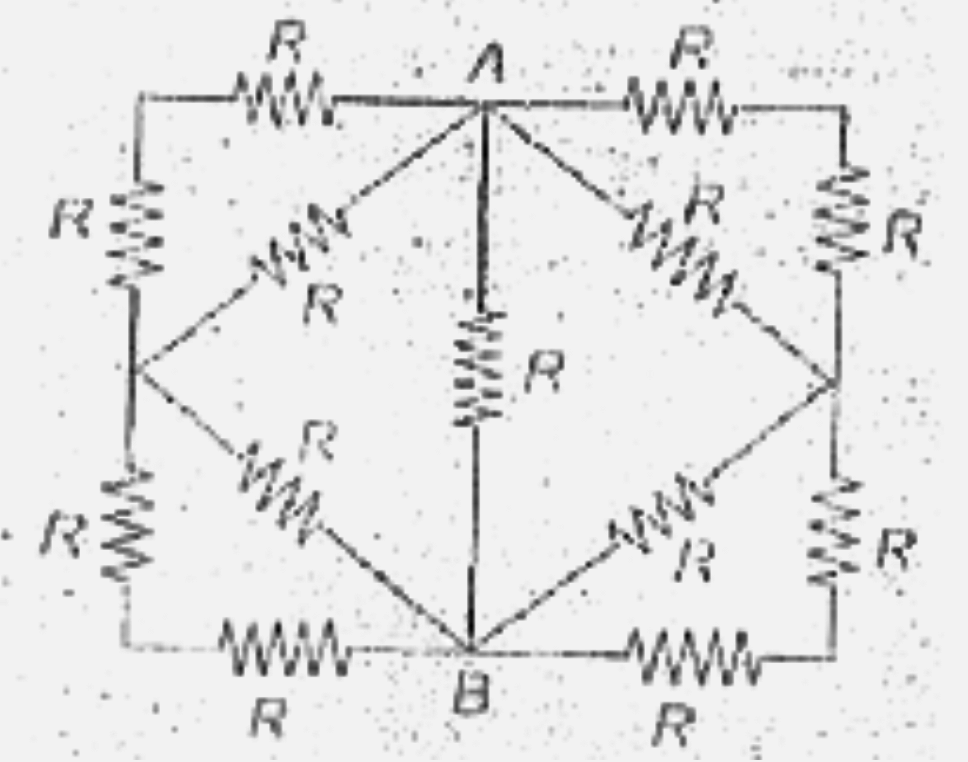
View SolutionThirteen resistors each of resistance R are connected in the circuit as shown . The effective resistance between A and B is
View Solutionn equal resistors are first connected in series and then connected in parallel. What is the ratio of the maximum to the minimum resistance ?
View Solution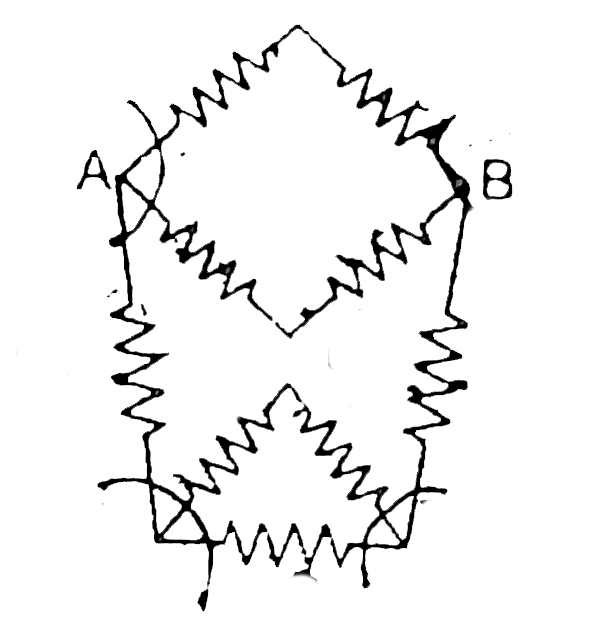
If resistance of each resistor is R then the effective resistance between A&B of the shown network is:
View SolutionTwo resistors of 2.092 and 3.0 22 are connected
in series. Find the effective resistance of combination .
View SolutionSix resistors each of resistance R and two resistors each of resistance r are connected in the network shown below. The equivalent resistance between A and B is
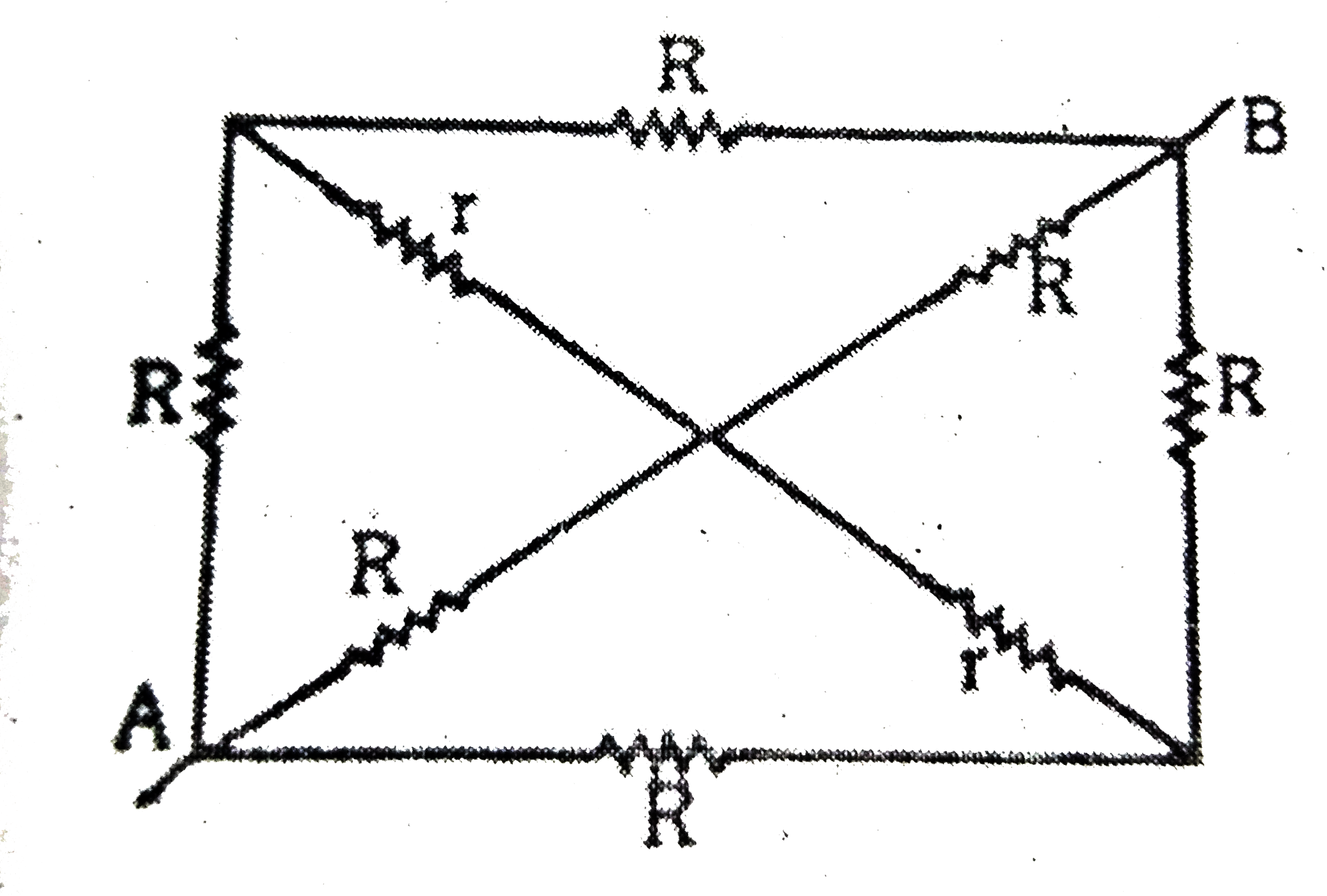
View SolutionA set of n identical resistors, each of resistance RΩ, when connected in series have an effective resistance XΩ and when the resistors are connected in parallel, their effective resistance is YΩ. Find the relation between R, X and Y.
View SolutionA student has 10 resistors of resistance ‘ r ’. The minimum resistance made by him from given resistors is
View SolutionWhich combination gives maximum number of products?
View Solution

