For infinite ladder network containing identical resistance of RΩ each, are combined as shown in figure. The equivalent resistance between A and B is RAB and between A and C is RAC. Then the value RABRAC is :

34
43
2
12
The correct Answer is:A
Let the equivalent resistance of one infinite ladder be x. Then the complete network reduces to

∴RAB=x×3xx+3x=34x
and RAC=2x×2x2x+2x=x
Hence RABRAC=34
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.48
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.49
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.46
11 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
In the network shown in the figure, the equivalent resistance between A and C is
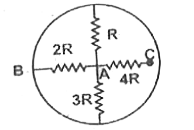
View SolutionFour identical resistances each having value R are arranged as shown in Figure. Find the equivalent resistance between A and B.

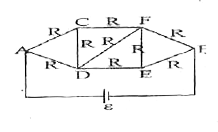
View SolutionIdnetical resistor each of resistance r are connected as shown in figure. Calculate equivalent resistance between A and E.
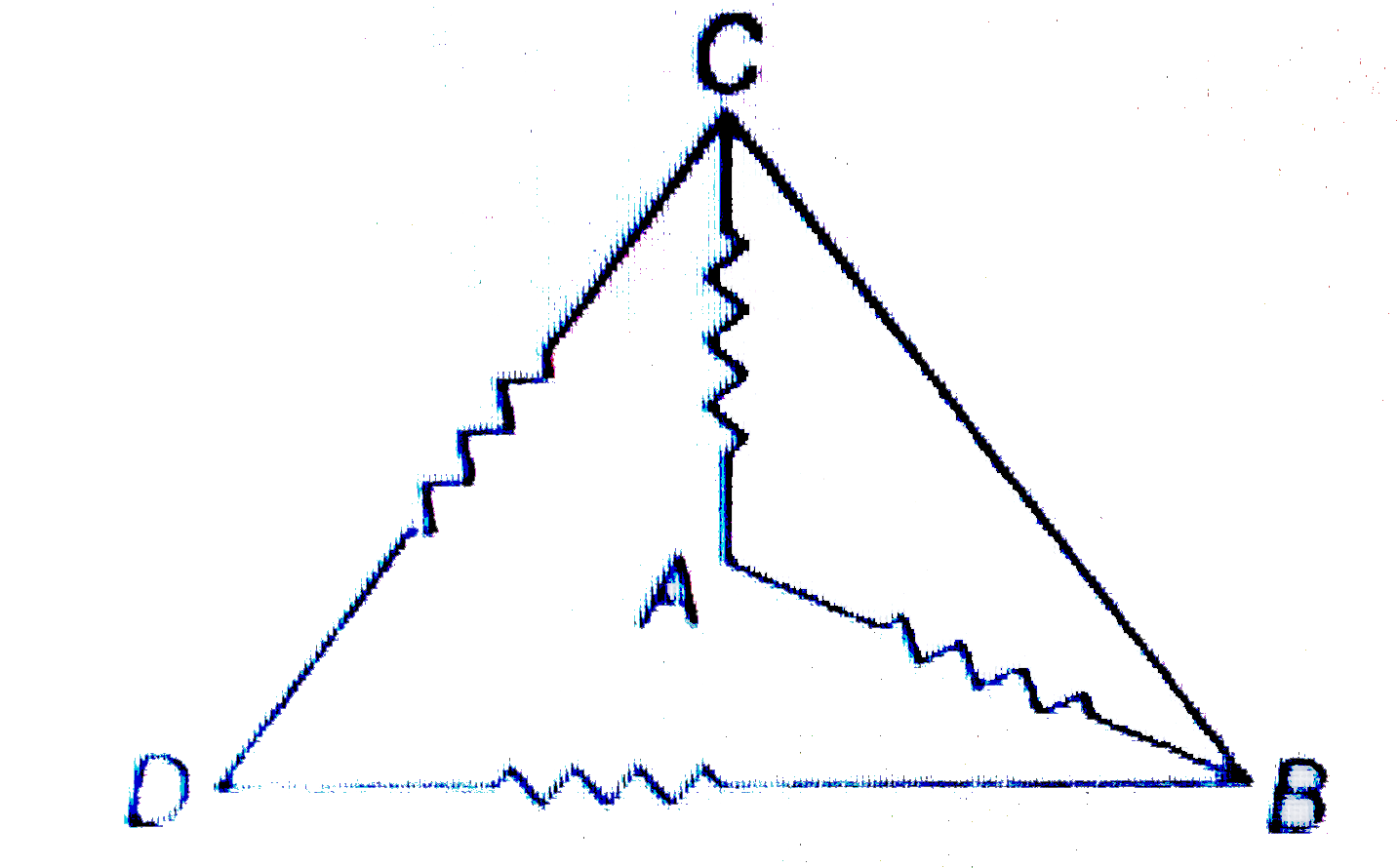
View SolutionEach resistance of the circuit shown in figure is r. The equivalent resistance between A and B is
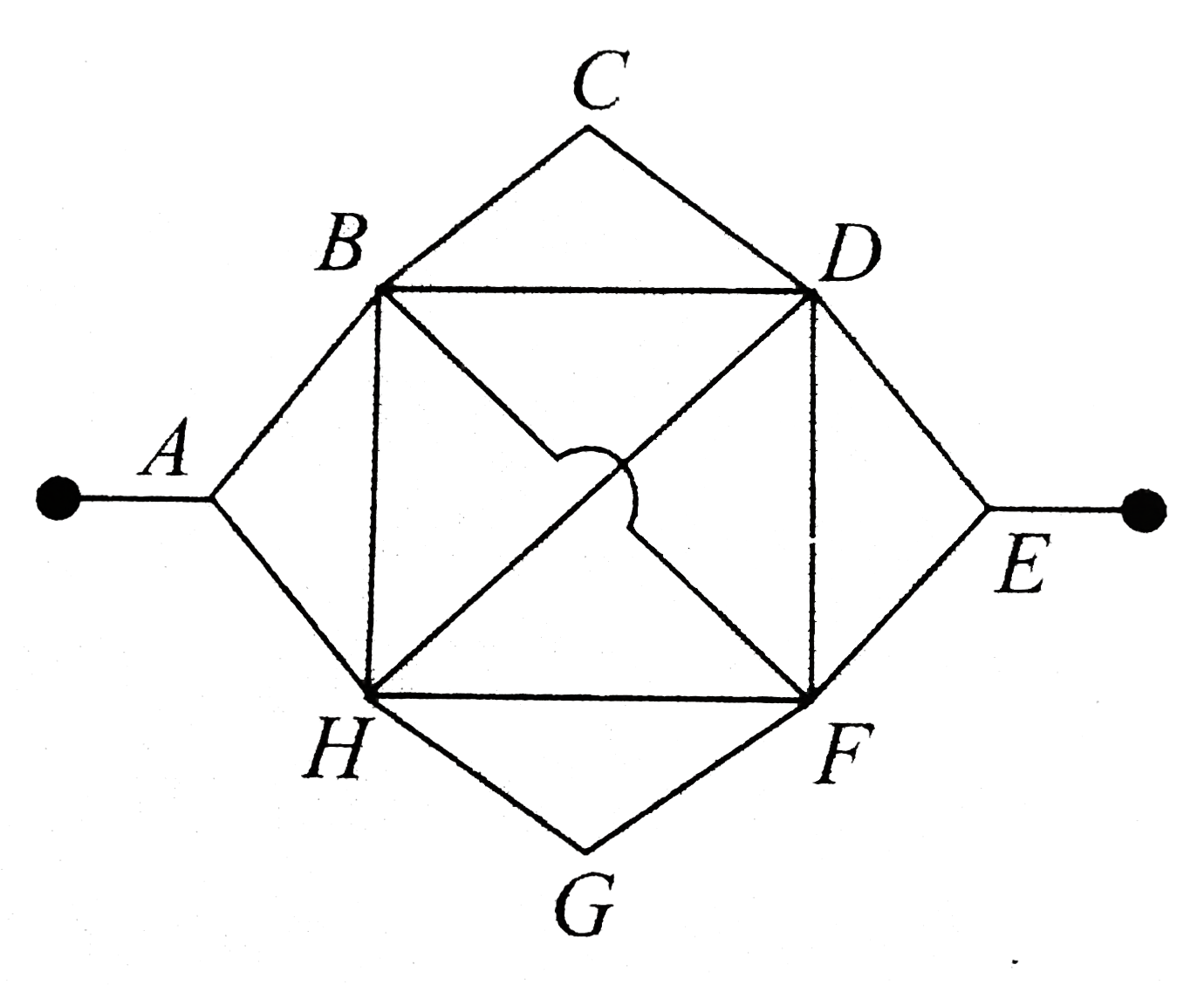
View SolutionA frame is formed by nine identical wires of resistances R each as shown in the figure.
The equivalent resistance between A and B is
View SolutionSix equal resistance,eacch of resistance R are connected as shown in the figure.Equivalent resistance between P and Q is
_PHY_E05_276_Q01.png)
View SolutionInside a supeerconducting ring, six identical resistors each of resistance R are connected as shown in figure. The equivalent resistances.
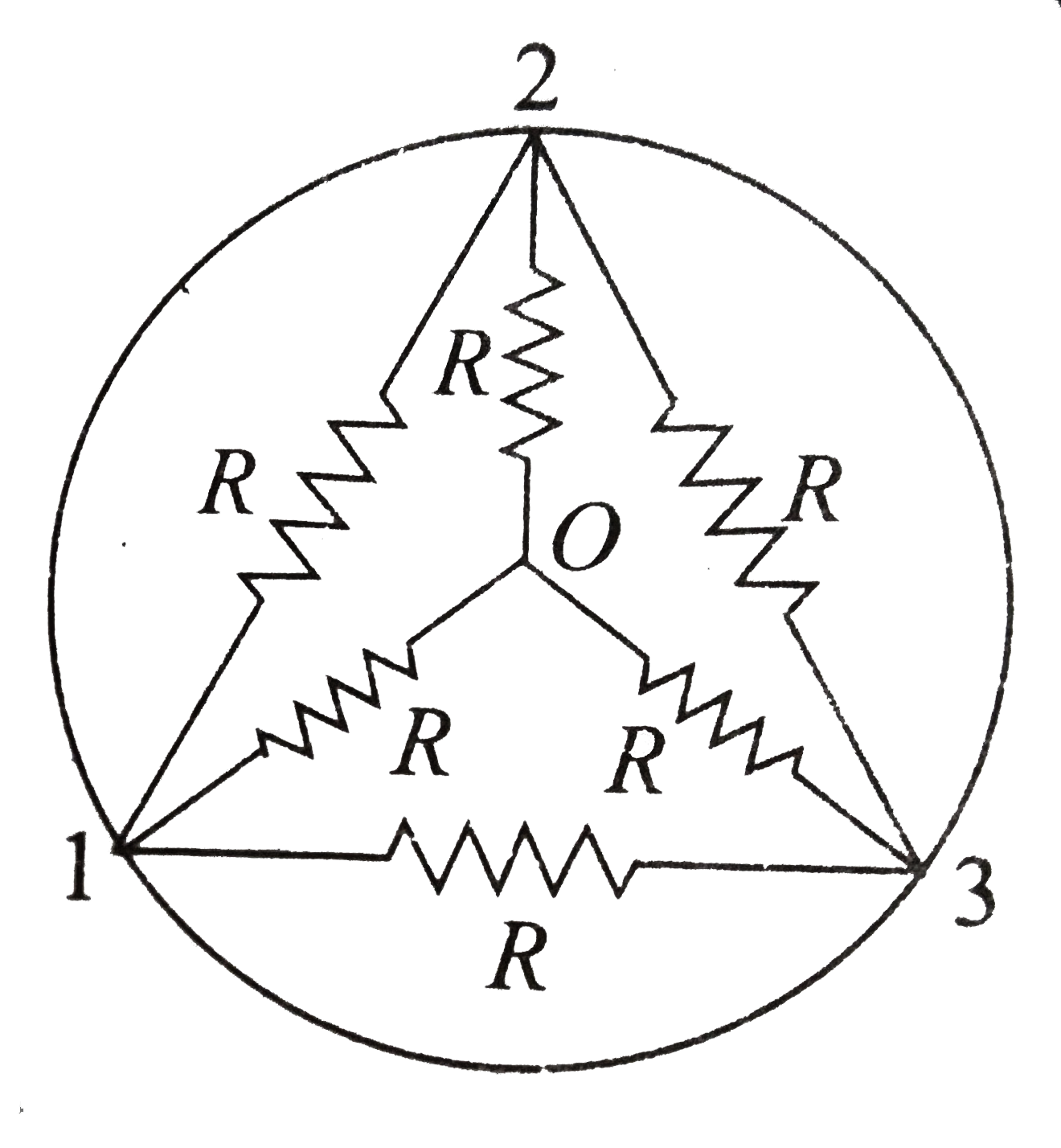
View SolutionIn the netwrok shown in fig. each resistance is R.

The equivalent resistance between A and B is
View SolutionIn the netwrok shown in fig. each resistance is R.

The equivalent resistance between A and G is
View SolutionEach of the resistor shown in fig. has resistance R. Find the equivalent resistance between A and B
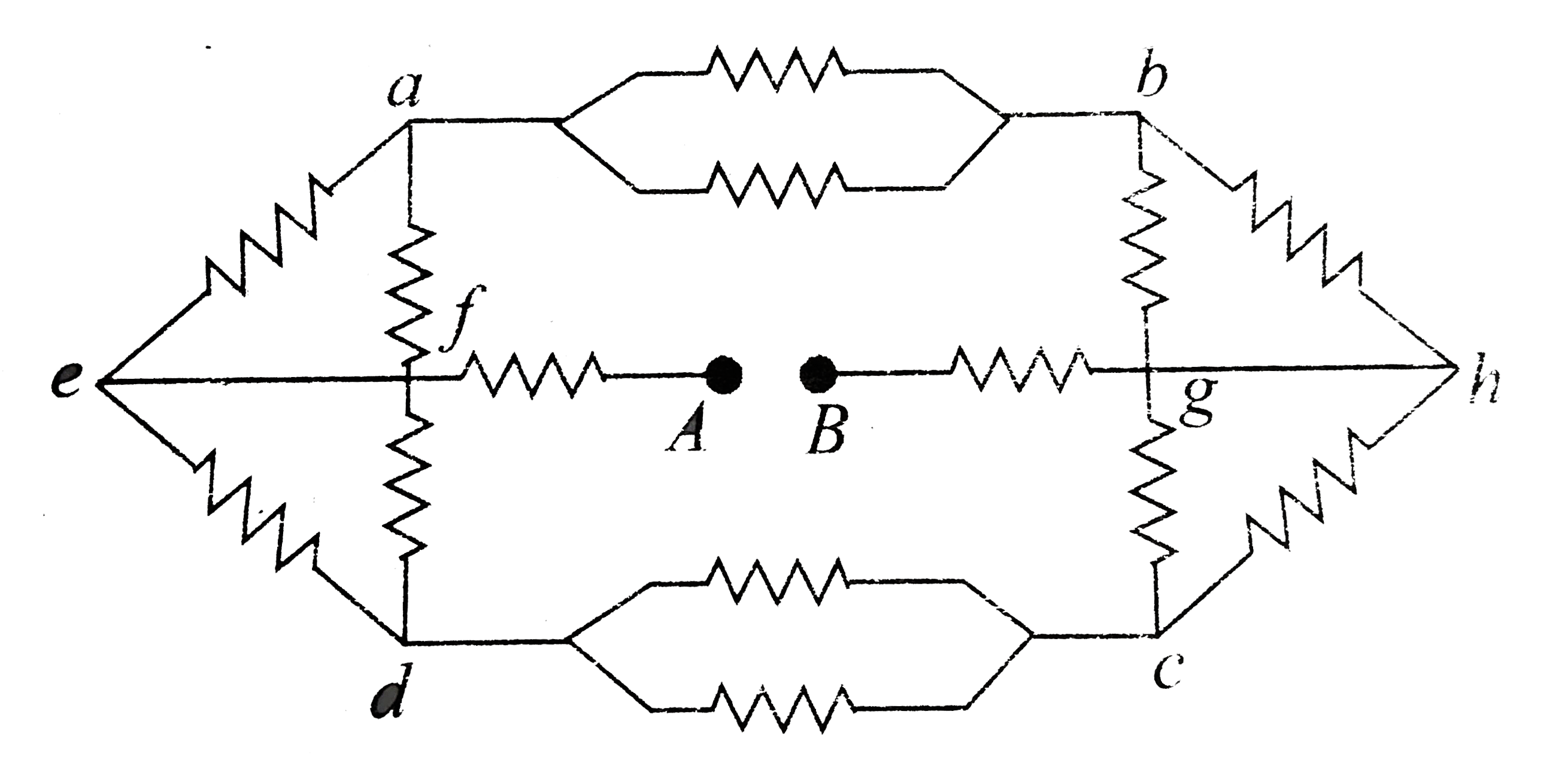
View Solution
