A charged is moving with constant velocity parallel to a horizontal current carrying long wire. The direction of velocity of that particle and the current are same. If the force acting on the particle are only magnetic force due to wire and gravitational force due to earth, then the particle :
must be positively charged
must be negatively charged
may be positively charged
may be neutral
The correct Answer is:C
To solve the problem, we need to analyze the forces acting on a charged particle moving parallel to a long current-carrying wire. The key forces to consider are the magnetic force due to the wire and the gravitational force due to the Earth.
1. Identify the Direction of Current and Velocity:
- The charged particle is moving with a constant velocity parallel to the wire, and both the particle's velocity and the current are in the same direction.
2. Determine the Direction of the Magnetic Field:
- According to the right-hand rule, if you point your thumb in the direction of the current (I), your fingers will curl in the direction of the magnetic field (B). For a long straight wire, the magnetic field circles around the wire.
- If the current is flowing horizontally to the right, the magnetic field at the location of the particle (above the wire) will be directed out of the plane (upward).
3. Calculate the Magnetic Force:
- The magnetic force (F_B) on a charged particle moving in a magnetic field is given by the formula:
FB=Q(v×B)
- Here, Q is the charge of the particle, v is the velocity vector, and B is the magnetic field vector.
- Since both the velocity and the magnetic field are in the same plane (horizontal for velocity and vertical for magnetic field), we can use the right-hand rule to determine the direction of the magnetic force.
4. Direction of the Magnetic Force:
- Using the right-hand rule for the cross product v×B:
- Point your fingers in the direction of v (to the right).
- Curl your fingers in the direction of B (upward).
- Your thumb will point downward, indicating that the magnetic force FB acts downward.
5. Consider the Gravitational Force:
- The gravitational force Fg acting on the particle is directed downward and is equal to mg, where m is the mass of the particle and g is the acceleration due to gravity.
6. Net Force and Constant Velocity:
- Since the particle is moving with constant velocity, the net force acting on it must be zero. This means that the upward forces must balance the downward forces.
- The gravitational force Fg is downward, and the magnetic force FB is also downward. For the net force to be zero, there must be an upward force acting on the particle.
7. Determine the Charge of the Particle:
- Since we need an upward magnetic force to balance the downward gravitational force, the charge Q must be negative. This is because a negative charge moving in a magnetic field (with the given directions) will experience an upward force.
Conclusion:
Thus, the charge of the particle must be negative for the forces to balance and for the particle to move with constant velocity.
- The charged particle is moving with a constant velocity parallel to the wire, and both the particle's velocity and the current are in the same direction.
- According to the right-hand rule, if you point your thumb in the direction of the current (I), your fingers will curl in the direction of the magnetic field (B). For a long straight wire, the magnetic field circles around the wire.
- If the current is flowing horizontally to the right, the magnetic field at the location of the particle (above the wire) will be directed out of the plane (upward).
- The magnetic force (F_B) on a charged particle moving in a magnetic field is given by the formula:
FB=Q(v×B)
- Here, Q is the charge of the particle, v is the velocity vector, and B is the magnetic field vector.
- Since both the velocity and the magnetic field are in the same plane (horizontal for velocity and vertical for magnetic field), we can use the right-hand rule to determine the direction of the magnetic force.
- Using the right-hand rule for the cross product v×B:
- Point your fingers in the direction of v (to the right).
- Curl your fingers in the direction of B (upward).
- Your thumb will point downward, indicating that the magnetic force FB acts downward.
- The gravitational force Fg acting on the particle is directed downward and is equal to mg, where m is the mass of the particle and g is the acceleration due to gravity.
- Since the particle is moving with constant velocity, the net force acting on it must be zero. This means that the upward forces must balance the downward forces.
- The gravitational force Fg is downward, and the magnetic force FB is also downward. For the net force to be zero, there must be an upward force acting on the particle.
- Since we need an upward magnetic force to balance the downward gravitational force, the charge Q must be negative. This is because a negative charge moving in a magnetic field (with the given directions) will experience an upward force.
Thus, the charge of the particle must be negative for the forces to balance and for the particle to move with constant velocity.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.48
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.49
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.46
11 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
When two wires have current in same direction then force is
View SolutionTo keep a particle moving with constant velocity on a frictionless horizontal surface an external force
View SolutionThe force between two parallel current carrying wires is independent of
View SolutionIn the figure PQ is a long current carrying wire which is placed near a current carrying coil. The direction of the force acting on PQ will be

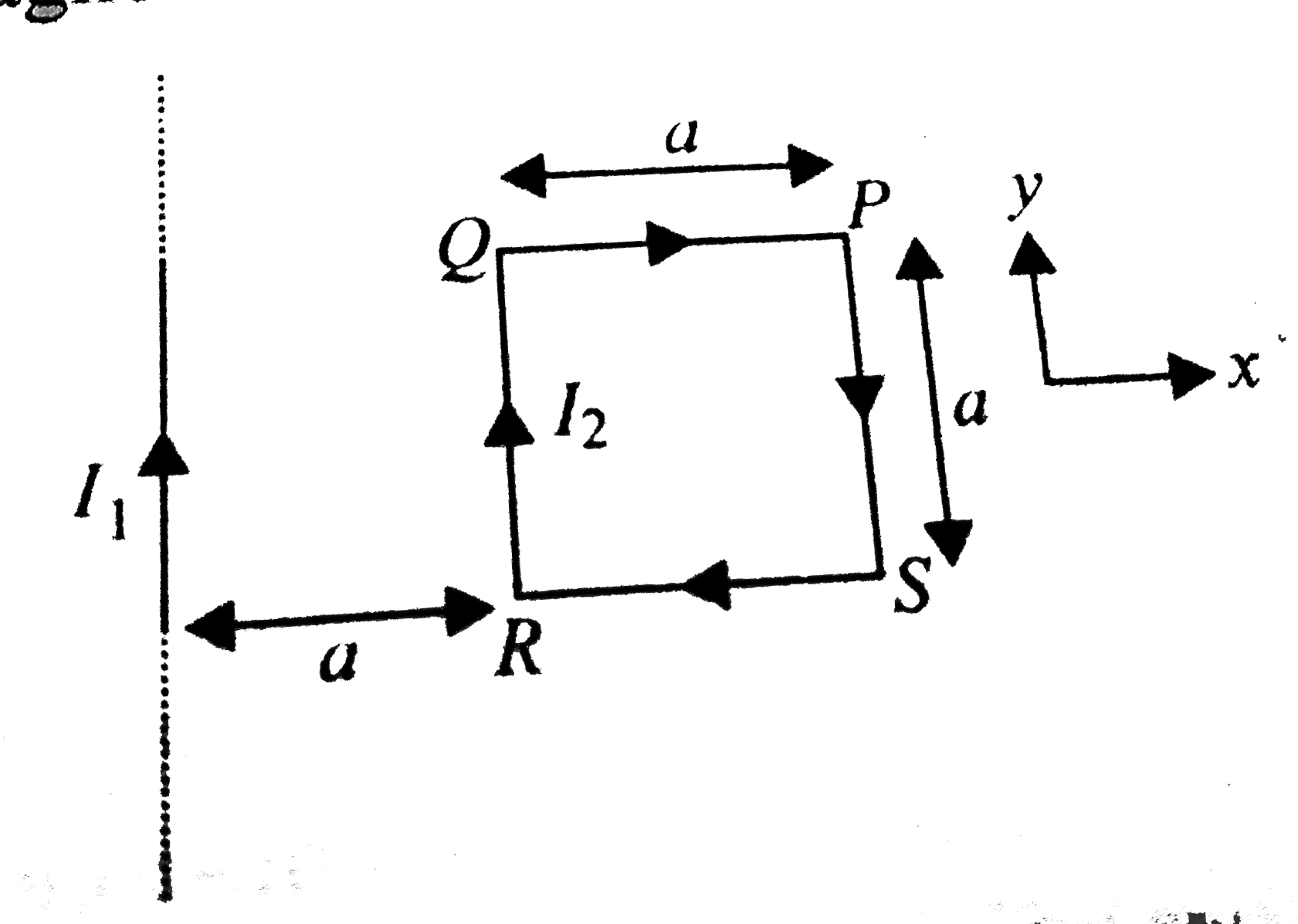
View SolutionFind the magnetic force on loop PQRS due to the wire.
View SolutionSelect the correct statement :(Only force on a particle is due to electric field)
View SolutionA charged particle enters into a space and continues to move undeflected. Considering gravitational force also on the particle, in the space
View SolutionMagnetic lines of force due to a straight conductor carrying current are
View SolutionWhen two parallel wires carrying current l and 2l in same direction are placed at a distance d apart, the ratio of force per unit length acting upon the wire due to other is
View SolutionA particle moving with velocity →V is acted by the three forces shown by the vector triangle PQR. The velocity of the particle will :

View Solution
