Space between tow concentric spheres of radii r1andr2 such that r1<r2 is filled with a material of resistivity ρ. Find the resistance between inner and outer surface of the material
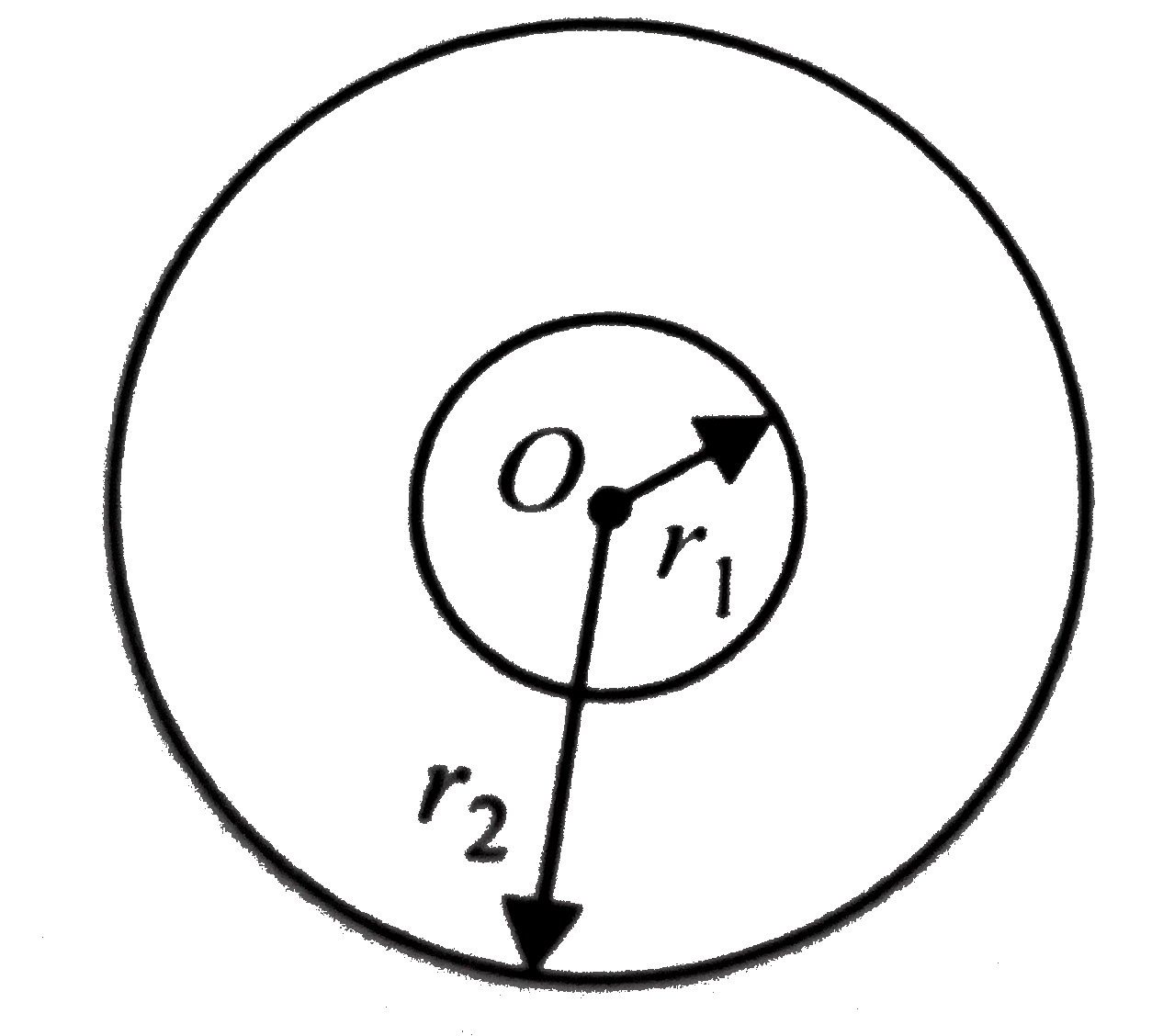
r1r2p2
r2−r1r1r2p4π
r1r2r2−r1p4π
none of these.
The correct Answer is:B
Since, R=ρla∴R=ρ=dl4πl2 (where l is any radius and dl is small element).
R=ρ4πr2∫r1dll2=ρ4π[−1l]r2r1=ρ4π[1r1−1r2]
R=[r2−r1r1r2]ρ4π
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:NCERT FINGERTPS ENGLISHChapter:CURRENT ELECTRICITYExercise:DRIFT OF ELECTRONS
Explore 2 Videos
- CURRENT ELECTRICITYBook:NCERT FINGERTPS ENGLISHChapter:CURRENT ELECTRICITYExercise:LIMITATIONS OF OHM S LAW
Explore 4 Videos
- CURRENT ELECTRICITYBook:NCERT FINGERTPS ENGLISHChapter:CURRENT ELECTRICITYExercise:ELECTRIC CURRENT IN CONDUCTORS
Explore 2 Videos
- COMMUNITCATION SYSTEMSBook:NCERT FINGERTPS ENGLISHChapter:COMMUNITCATION SYSTEMSExercise:Assertion And Reason
Explore 30 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:NCERT FINGERTPS ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
Knowledge Check
Two soap bubbles A and B have radii r1andr2 respectively. If r1<r2 than the excess pressure inside
Abubbles A and B will be equalBbubbles A will be less than that in bubbles BCbubbles A will be greater than that in bubble BDbubbles A and B will be zero.
Sphere of inner radius a and outer radius b is made of p uniform resistivity find resistance between inner and outer surface
View SolutionTwo thin metallic spherical shells of radii r1 and r2 (r1<r2) are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shells is maintained at temperature θ1 .and the outer shell at temperature θ2 (θ1<θ2). Calculate the rate at which heat flows radially through the material.

View SolutionTwo thin metallic spherical shells of radii r1 and r2 (r1<r2) are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shells is maintained at temperature θ1 and the outer shell at temperature θ2 (θ1<θ2). Calculate the rate at which heat flows radially through the material.

View SolutionA coaxial cable is made up of two conductors. The inner conductor is solid is of radius R1 and the outer coductor is hollow of inner radius R2 and outer radius R3 . The space between the conductors are carrying currents of equal magnitudes and in oppsite direactions. then the variation of magnetic field with distance form the axis is best plotted as :

View SolutionTwo thin conectric shells made of copper with radius r1 and r2(r2>r1) have a material of thermal conductivity K filled between them. The inner and outer spheres are maintained at temperature TH and TC respectively by keeping a heater of power P at the centre of the two sphers. Find the value of P.
View SolutionA spherical body of radius 'b' has a concentric cavity of radius 'a' as shown. Thermal conductivity of the material is K. Find thermal resistance between inner surface P and outer surface Q.

View SolutionConsider two concentric spherical metal shells of radii r1 and r2(r2>r1). If the outer shell has a charge q and the inner one is grounded, then the charge on the inner shell is
View Solution

