Two thin conectric shells made of copper with radius r1 and r2(r2>r1) have a material of thermal conductivity K filled between them. The inner and outer spheres are maintained at temperature TH and TC respectively by keeping a heater of power P at the centre of the two sphers. Find the value of P.
To find the power P supplied by the heater at the center of two concentric copper shells with radii r1 and r2 (where r2>r1), we can follow these steps:
Step 1: Understand the Setup
We have two concentric shells with an inner radius r1 and an outer radius r2. The inner shell is maintained at a temperature TH and the outer shell at TC. The heater at the center provides a power P to maintain these temperatures.
Step 2: Define the Heat Flow
The heat flows from the inner shell (higher temperature TH) to the outer shell (lower temperature TC). The rate of heat transfer can be expressed in terms of thermal current I, which is equivalent to the power P supplied by the heater.
Step 3: Calculate the Thermal Resistance
The thermal resistance R of the material between the shells can be calculated using the formula:
R=LkA
where:
- L is the thickness of the shell,
- k is the thermal conductivity of the material,
- A is the cross-sectional area.
For a thin shell, the thickness dx can be integrated from r1 to r2.
Step 4: Set Up the Integral for Resistance
The differential thermal resistance dR can be expressed as:
dR=dxk⋅4πx2
Integrating this from r1 to r2:
R=∫r2r1dxk⋅4πx2
Step 5: Perform the Integration
The integral simplifies to:
R=14πk(−1x)∣∣∣r2r1=14πk(−1r2+1r1)=14πk(1r1−1r2)
Step 6: Substitute the Resistance into the Heat Current Equation
The heat current (or power P) can be expressed as:
I=ΔTR
where ΔT=TH−TC. Substituting for R:
P=TH−TCR=(TH−TC)⋅4πk⋅r1r2r2−r1
Final Result
Thus, the power P supplied by the heater is given by:
P=(TH−TC)⋅4πkr1r2r2−r1
We have two concentric shells with an inner radius r1 and an outer radius r2. The inner shell is maintained at a temperature TH and the outer shell at TC. The heater at the center provides a power P to maintain these temperatures.
The heat flows from the inner shell (higher temperature TH) to the outer shell (lower temperature TC). The rate of heat transfer can be expressed in terms of thermal current I, which is equivalent to the power P supplied by the heater.
The thermal resistance R of the material between the shells can be calculated using the formula:
- L is the thickness of the shell,
- k is the thermal conductivity of the material,
- A is the cross-sectional area.
The differential thermal resistance dR can be expressed as:
The integral simplifies to:
The heat current (or power P) can be expressed as:
Thus, the power P supplied by the heater is given by:
Topper's Solved these Questions
- HEAT TRANSFERBook:RESONANCE ENGLISHChapter:HEAT TRANSFERExercise:Board Level Exercise
Explore 14 Videos
- HEAT TRANSFERBook:RESONANCE ENGLISHChapter:HEAT TRANSFERExercise:Exercise-1
Explore 1 Video
- HEAT TRANSFERBook:RESONANCE ENGLISHChapter:HEAT TRANSFERExercise:Advancel Level Problems
Explore 17 Videos
- GRAVITATIONBook:RESONANCE ENGLISHChapter:GRAVITATIONExercise:Exercise
Explore 21 Videos
- KINEMATICSBook:RESONANCE ENGLISHChapter:KINEMATICSExercise:Exercise
Explore 65 Videos
Similar Questions
Two thin metallic spherical shells of radii r1 and r2 (r1<r2) are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shells is maintained at temperature θ1 .and the outer shell at temperature θ2 (θ1<θ2). Calculate the rate at which heat flows radially through the material.

View SolutionTwo thin metallic spherical shells of radii r1 and r2 (r1<r2) are placed with their centres coinciding. A material of thermal conductivity K is filled in the space between the shells. The inner shells is maintained at temperature θ1 and the outer shell at temperature θ2 (θ1<θ2). Calculate the rate at which heat flows radially through the material.

View Solution
Knowledge Check
Space between tow concentric spheres of radii r1andr2 such that r1<r2 is filled with a material of resistivity ρ. Find the resistance between inner and outer surface of the material
 Ar1r2p2Br2−r1r1r2p4πCr1r2r2−r1p4πDnone of these.
Ar1r2p2Br2−r1r1r2p4πCr1r2r2−r1p4πDnone of these.
A hollow tube has a length l, inner radius R1 and outer radius R2 . The material has a thermal conductivity K. Find the heat flowing through the walls of the tube if (a) the flat ends are maintained at temperature T1 and T2(T2>T1) (b) the inside of the tube is maintained at temperature T1 and the outside is maintained at T2 .
View SolutionConsider two concentric spherical metal shells of radii r1 and r2(r2>r1). If the outer shell has a charge q and the inner one is grounded, then the charge on the inner shell is
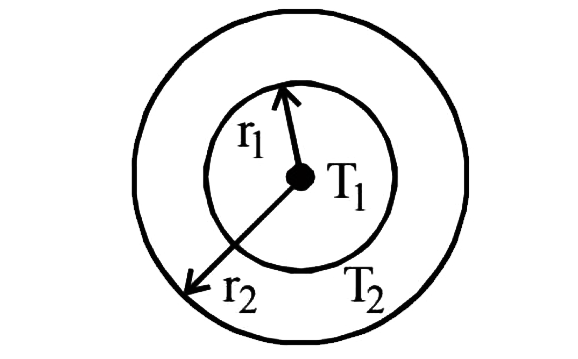
View SolutionThe figure shows a system of two concentric spheres of radii r1andr2 are kept at temperature T1andT2, respectively. The radial rate of flow of heat in a substance between the two concentric spheres is proportional to
View SolutionA hollow metallic sphere of radius 20cm surrounds a concentric metallic sphere of radius 5cm. The space between the two sphere is filled with a nonmetallic material. The inner and outer sphere are maintained at 50∘C and 10∘C respectively and it is found that 100J of heat passes from the inner sphere to the outer sphere per second. Find the thermal conductivity of the material between the sphere.
View SolutionA cylinder of radius r made of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius r and outer radius 2r made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. Show that the effective thermal conductivity of the system is (K1+3K2)/4.
View SolutionTwo concentric spherical shells of radius R1 and R2(R2>R1) are having uniformly distributed charges Q1 and Q2 respectively. Find out total energy of the system.

View SolutionA cylinder of radius R made of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 2R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. The effective thermal conductivity of the system is
View Solution