A cord of mass m length L, area of cross section A and Young's modulus y is hanging from a ceiling with the help of a rigid support. The elogation developed in the wire due to its own weight is
mglYA
mgl2YA
2mglYA
2mgl3YA
To find the elongation developed in a cord of mass m, length L, area of cross-section A, and Young's modulus Y due to its own weight, we can follow these steps:
1. Identify the Effective Length:
The weight of the cord acts at its center of mass, which is located at the midpoint of the cord. Therefore, the effective length Leff for the elongation calculation is:
Leff=L2
2. Calculate the Force Acting on the Cord:
The force acting on the cord due to its own weight is given by:
F=mg
where g is the acceleration due to gravity.
3. Use Young's Modulus Formula:
Young's modulus Y is defined as:
Y=StressStrain=F/AΔL/L
Rearranging this gives:
ΔL=F⋅LA⋅Y
4. Substituting the Effective Length:
Since we are considering the effective length, we substitute L with Leff:
ΔL=F⋅(L/2)A⋅Y
5. Substituting the Force:
Now, substitute F=mg:
ΔL=(mg)⋅(L/2)A⋅Y
6. Final Expression for Elongation:
Simplifying this gives:
ΔL=mgL2AY
Thus, the elongation developed in the wire due to its own weight is:
ΔL=mgL2AY
The weight of the cord acts at its center of mass, which is located at the midpoint of the cord. Therefore, the effective length Leff for the elongation calculation is:
Leff=L2
The force acting on the cord due to its own weight is given by:
F=mg
where g is the acceleration due to gravity.
Young's modulus Y is defined as:
Y=StressStrain=F/AΔL/L
Rearranging this gives:
ΔL=F⋅LA⋅Y
Since we are considering the effective length, we substitute L with Leff:
ΔL=F⋅(L/2)A⋅Y
Now, substitute F=mg:
ΔL=(mg)⋅(L/2)A⋅Y
Simplifying this gives:
ΔL=mgL2AY
ΔL=mgL2AY
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:APPLICATIONS OF ELASTIC BEHAVIOUR OF MATERIALS
Explore 8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:HOTS
Explore 8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:STRESS-STRAIN CURVE
Explore 5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:NCERT Exemplar
Explore 5 Videos
- MOTION IN A PLANE Book:NCERT FINGERTPS ENGLISHChapter:MOTION IN A PLANE Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
wire of length I has a ear mass density λ and area of cross-section A and the Young's modulus y is suspended vertically from rigid support. The extension produced in wire due to its own weight
View SolutionA uniform rod of length 2L, area of cross - section A and Young's modulus Y is lying at rest under the action of three forces as shown.
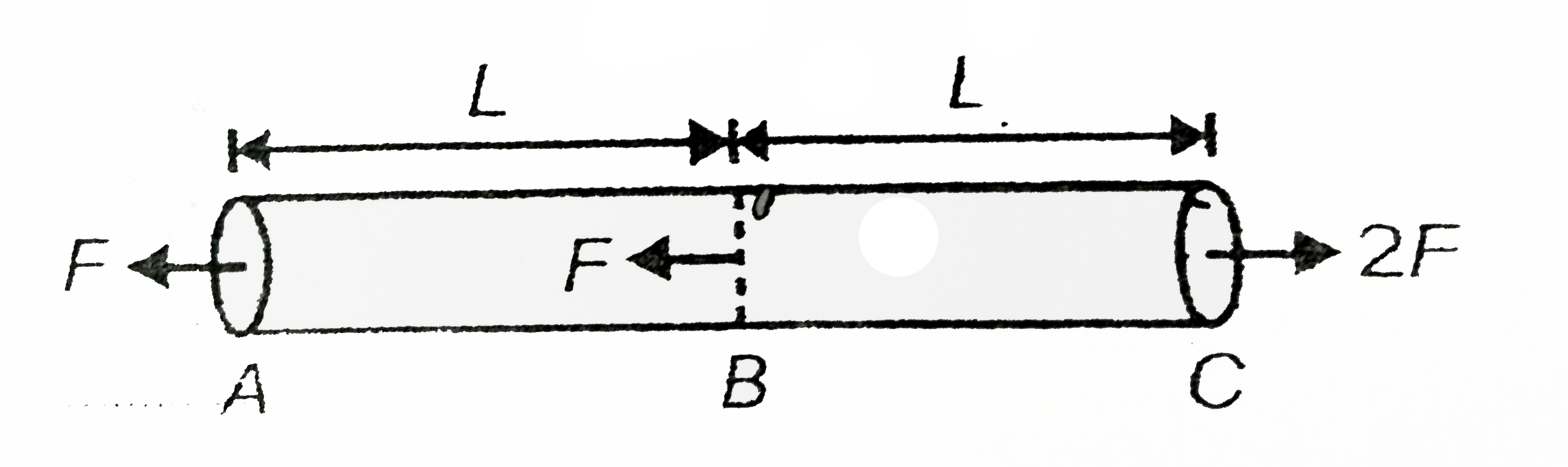
Select the correct alternatives.
View SolutionA block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
View SolutionA wire of length l, area of cross section A and Young’s modulus of elasticity Y is stretched by a longitudinal force F. The change in length is Δl Match the following two columns.
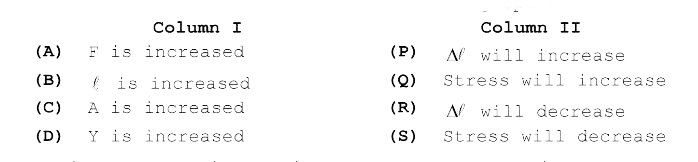
View SolutionA wire of length l, area of cross-section A and Young,s modulus of elasticity Y is suspended form the roof of a building. A block of mass m is attached at lower end of the wire. If the block is displaced from its mean position and released then the block starts oscillating. Time period of these oscillations will be

View SolutionA uniform cylindrical rod of length L, cross-section area A and Young's modulus Y is acted upon by the force as shown in Fig. 7(CF).3. The elongation of the rod is
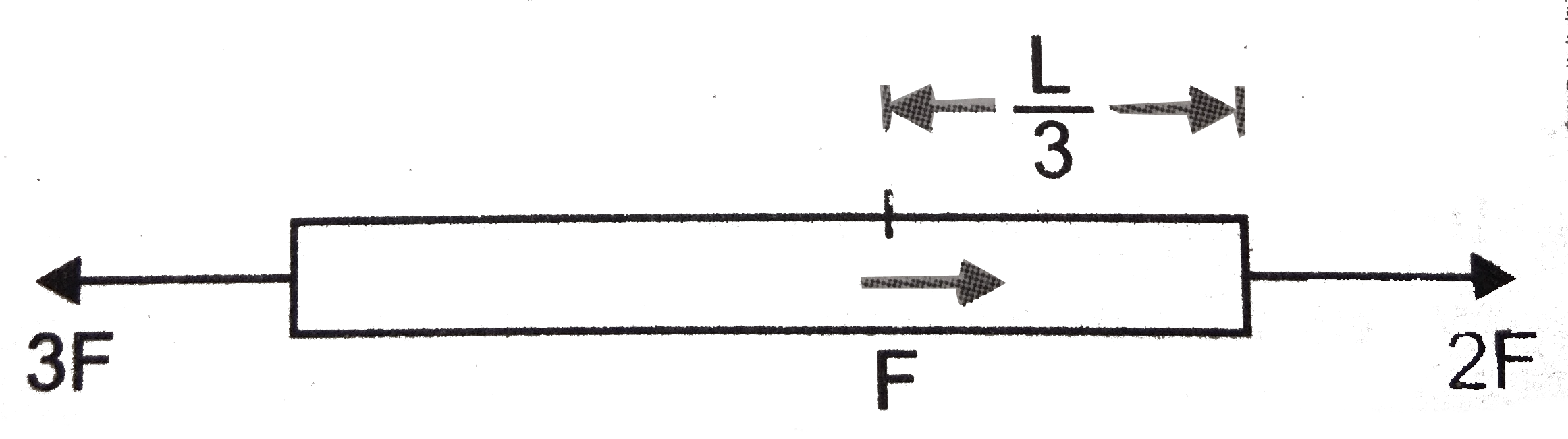
View SolutionA thick rope of density ρ and length L is hung from a rigid support. The increase in length of the rope due to its own weight is (Y is the Young's modulus)
View SolutionA metal wire of length L, area of cross-section A and young's modulus Y is stretched by a variable force F such that F is always slightly greater than the elastic forces of resistance in the wire. When the elongation of the wire is l
View SolutionA chain of length 'L' and mass 'M' is hanging by fixing its upper end to a rigid support. The tension in the chain at a distance 'x' from the rigid support is
View SolutionAn object of mass m is suspended at the end of a massless wire of length L and area of cross -section A. Young modulus of the material of the wire is Y. If the mass is pulled down slightly its frequency of oscillation along the vertical direction is :
View Solution

