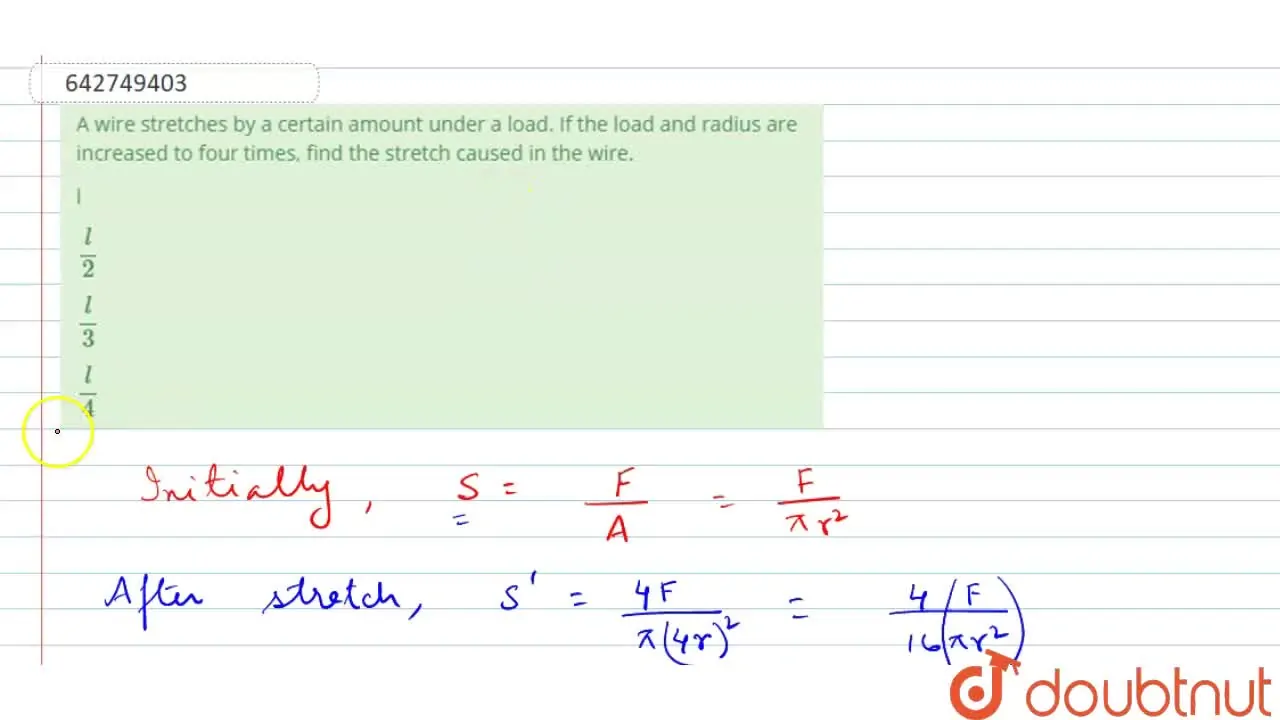
A wire stretches by a certain amount under a load. If the load and radius are increased to four times, find the stretch caused in the wire.
l
l2
l3
l4
The correct Answer is:D
Young's modulus, Y=WA×Ll
∴ Elongation , l=WLAY=WLπr2Y=l4
When both load and radius are increased to four times, the elongaation becomes
l'=4W×Lπ(4r)2×Y=WL4πr2Y=l4
Related Playlists
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - APPLICATIONS OF ELASTIC BEHAVIOUR OF MATERIALS8videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - HOTS8videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - STRESS-STRAIN CURVE5videos
MECHANICAL PROPERTIES OF SOLIDS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT Exemplar5videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason15videos
MOTION IN A PLANE
Similar Questions
If a wire is stretched to four times its length, then the specific resistance of the wire will
View SolutionA steel wire of length l and cross sectional area A is stretched by 1 cm under a given load. When the same load is applied to another steel wire of double its length and half of its cross section area, the amount of stretching (extension) is
View SolutionA wire is stretched to n times its length. Then the resistance now will be increase by
View SolutionEnergy of a stretched wire is
View SolutionA steel wire is stretched by 1kgwt. If the radius of the wire is doubled, its Young's modulus will
View SolutionA wire 0.5 m long vibrates 100 times a second. If the length of the wire is shortened to 0.4 in and the stretching force is increased to 4 times its original value what will be the new frequency?
View SolutionOne end of a metal wire is fixed to a ceiling and a load of 2 kg hangs from the other end. A similar wire is attached to the bottom of the load and another load of 1 kg hangs from this lower wire. Find the longitudinal strain in both wires. Area of cross section of each wire is 0.005cm2 and Young modulus of the metal is 2.0×1011Nm−2. Take g=10ms−2
View SolutionWhen a wire of length 5m and diameter 1mm was stretched by a load of 5kg the elongation produced in the wire was 1mm. Find the energy stored in per unit volume of the wire?
View SolutionA wire is stretched by one mm by a force of 1 kN. The work done is stretching the wire is
View SolutionWhen a wire is stretched to double its length, then
View Solution