A steel wire can support a maximum load of W before reaching its elastic limit. How much load can another wire, made out of identical steel, but with a radius one half the radius of the first wire, support before reaching its elastic limit?
W
W4
W4
4W
The correct Answer is:C
To solve the problem, we need to determine how much load a second wire, made of identical steel but with a radius that is half the radius of the first wire, can support before reaching its elastic limit.
1. Understand the Given Information:
- The first wire can support a maximum load W before reaching its elastic limit.
- The radius of the first wire is r.
- The radius of the second wire is r2=12r.
2. Calculate the Cross-Sectional Area:
- The cross-sectional area A1 of the first wire is given by:
A1=πr2
- The cross-sectional area A2 of the second wire is:
A2=πr22=π(12r)2=π(14r2)=πr24
3. Determine the Stress in Each Wire:
- The stress σ1 in the first wire when the load W is applied is:
σ1=WA1=Wπr2
- For the second wire, let the maximum load it can support be W′. The stress σ2 in the second wire is:
σ2=W′A2=W′πr24=4W′πr2
4. Equate the Stresses:
- Since both wires are made of identical steel and are subjected to the same elastic limit, the stresses must be equal:
σ1=σ2
Wπr2=4W′πr2
5. Solve for W′:
- Cancel πr2 from both sides:
W=4W′
- Rearranging gives:
W′=W4
6. Conclusion:
- The second wire can support a maximum load of W4 before reaching its elastic limit.
Final Answer:
The second wire can support a maximum load of W4.
- The first wire can support a maximum load W before reaching its elastic limit.
- The radius of the first wire is r.
- The radius of the second wire is r2=12r.
- The cross-sectional area A1 of the first wire is given by:
A1=πr2
- The cross-sectional area A2 of the second wire is:
A2=πr22=π(12r)2=π(14r2)=πr24
- The stress σ1 in the first wire when the load W is applied is:
σ1=WA1=Wπr2
- For the second wire, let the maximum load it can support be W′. The stress σ2 in the second wire is:
σ2=W′A2=W′πr24=4W′πr2
- Since both wires are made of identical steel and are subjected to the same elastic limit, the stresses must be equal:
σ1=σ2
Wπr2=4W′πr2
- Cancel πr2 from both sides:
W=4W′
- Rearranging gives:
W′=W4
- The second wire can support a maximum load of W4 before reaching its elastic limit.
The second wire can support a maximum load of W4.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:APPLICATIONS OF ELASTIC BEHAVIOUR OF MATERIALS
Explore 8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:HOTS
Explore 8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:STRESS-STRAIN CURVE
Explore 5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:NCERT Exemplar
Explore 5 Videos
- MOTION IN A PLANE Book:NCERT FINGERTPS ENGLISHChapter:MOTION IN A PLANE Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
A steel wire of 1.5 m long and of radius 1 mm is attached with a load 3 kg at one end the other end of the wire is fixed it is whirled in a vertical circle with a frequency 2 Hz. Find the elongation of the wire when the weight is at the lowest position Y=2×1011N/m2 and (g=10m/s2)
View SolutionThe maximum load that a wire can sustain is W. If the wire is cut to half its value, the maximum load it can sustain is
View Solution
Knowledge Check
The maximum load a wire can withstand without breaking, when its length is reduced to half of its original length, will
Abe doubleBbe halfCbe four timesDremain same.A mild steel wire of length 2L is strethched, within its elastic limit horizontally between two pillars(figure). A mass of m is suspended form the midpont of the wire. Strain in the wire is
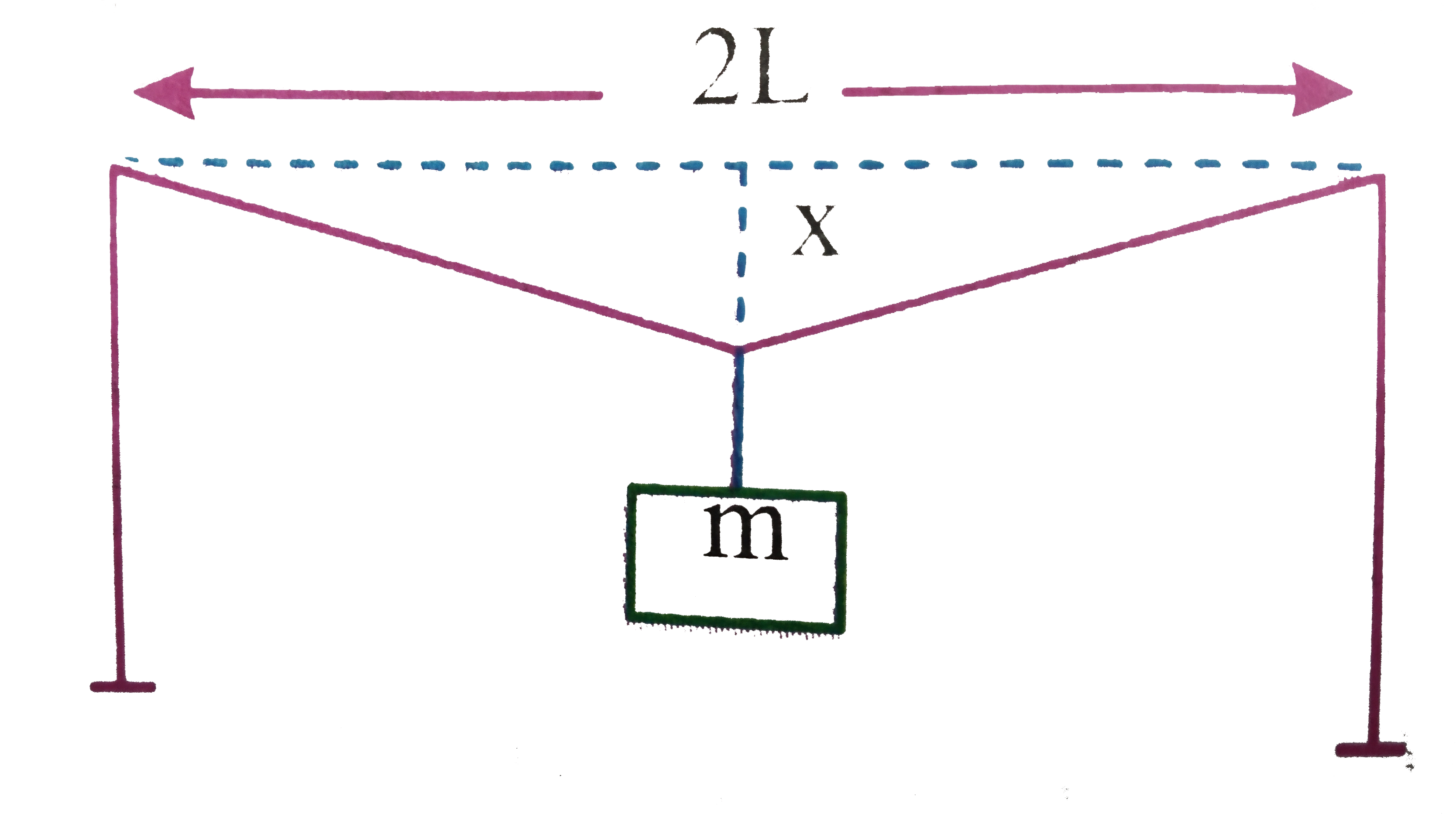 Ax22L2BxLCx2LDx22L
Ax22L2BxLCx2LDx22L
The elastic limit of brass is 379MPa. What should be the minimum diameter of a brass rod if it is to support a 400 N load without exceeding its elastic limit?
View SolutionAssertion Upto elastic limit of a stress-strain curve, the steel wire tends to regain its original shape when stress is removed.
Reason Within elastic limit, the wire follows Hooke's law.
View SolutionThe maximum load a wire can withstand without breaking, when its length is reduced to half of its original length, will
View SolutionA steel wire of length l and cross sectional area A is stretched by 1 cm under a given load. When the same load is applied to another steel wire of double its length and half of its cross section area, the amount of stretching (extension) is
View SolutionA mild steel wire of length 1.0m and cross sectional area 2L is strethched, within its elastic limit horizontally between two pillars(figure). A mass of m is suspended form the midpont of the wire. Strain in the wire is

View SolutionA piece of copper wire has twice the radius of a piece of steel wire. Young's modulus for steel is twice that of the copper. One end of the copper wire is joined to one end of the steel wire so that both can be subjected to the same longitudinal force. By what fraction of its length will the steel have stretched when the length of the copper has increased by 1%?
View Solution

