The ratio of shearing stress to the shearing strain is defined as
Young's modulus
bulk modulus
shear modulus
compressibility
The correct Answer is:C
To solve the question regarding the ratio of shearing stress to shearing strain, we can follow these steps:
Step 1: Understand the Definitions
- Shearing Stress (τ): This is defined as the force (F) applied parallel to the surface of a material divided by the area (A) over which the force is applied. Mathematically, it is expressed as:
τ=FA
- Shearing Strain (γ): This is defined as the change in the shape of the material due to the applied stress. It is the ratio of the displacement (x) to the height (h) of the material. Mathematically, it can be expressed as:
γ=xh
Step 2: Establish the Relationship
- The ratio of shearing stress to shearing strain is given by:
Shear Modulus (G)=Shearing StressShearing Strain=τγ
Step 3: Identify the Correct Term
- The term that describes this ratio is known as the Shear Modulus. It quantifies the material's response to shearing stress and is a measure of its rigidity.
Conclusion
- Therefore, the ratio of shearing stress to shearing strain is defined as the Shear Modulus.
Final Answer
The ratio of shearing stress to shearing strain is defined as Shear Modulus.
---
- Shearing Stress (τ): This is defined as the force (F) applied parallel to the surface of a material divided by the area (A) over which the force is applied. Mathematically, it is expressed as:
τ=FA
γ=xh
- The ratio of shearing stress to shearing strain is given by:
Shear Modulus (G)=Shearing StressShearing Strain=τγ
- The term that describes this ratio is known as the Shear Modulus. It quantifies the material's response to shearing stress and is a measure of its rigidity.
- Therefore, the ratio of shearing stress to shearing strain is defined as the Shear Modulus.
The ratio of shearing stress to shearing strain is defined as Shear Modulus.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:APPLICATIONS OF ELASTIC BEHAVIOUR OF MATERIALS
Explore 8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:HOTS
Explore 8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:STRESS-STRAIN CURVE
Explore 5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:NCERT Exemplar
Explore 5 Videos
- MOTION IN A PLANE Book:NCERT FINGERTPS ENGLISHChapter:MOTION IN A PLANE Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
Knowledge Check
The ratio of tensile stress to the longitudinal strain is defined as
AÂ bulk modulusBYoung's modulusCshear modulusDcompressibilityA bar of cross- sectional area A is is subjected two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB' making an angle θ with length. The ratio of tensile stress to the shearing stress on the plane BB' is
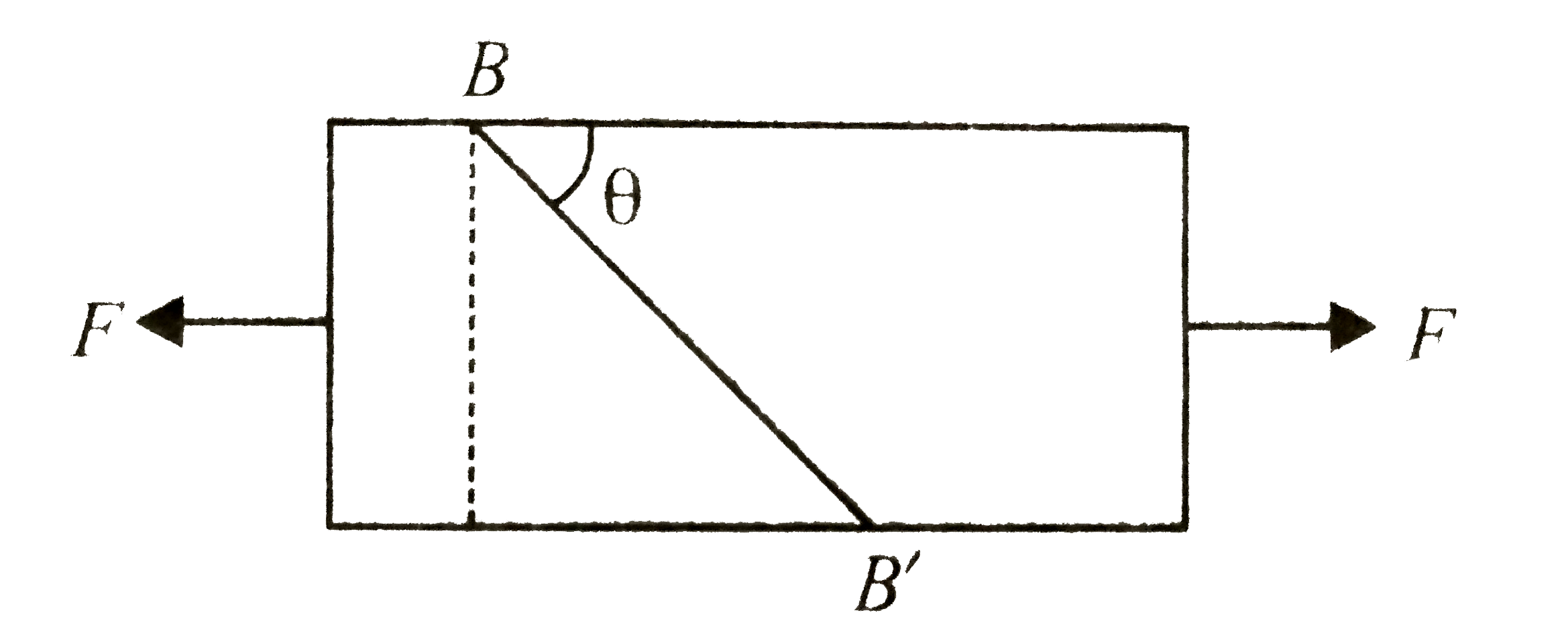 AtanθBsecθCcotθDcosθ
AtanθBsecθCcotθDcosθTwo strips of metal are riveted together at their ends by four rivets, each of diameter 6mm. What is the maximum tension that can be exterted by the riveted strip if the shearing stress on the rivet is not to exceed 6.9×107Pa? Assume that each rivet is to carry one quarter of the load .
A2×103NB3.9×103NC7.8×103ND15.6×103N
A wire of length 5m is twisted through 300 at free end If the radius of wire is 1mm , the shearing strain in the wire is
View Solution(A): Transverse mechanical waves can not propagates in liquids and gases.
(R): Liquids and gases flow when acted on by shearing stress, they can not sustain shear stress
View SolutionTwo strips of metal are riveted together at their ends by four rivets, each of diameter 6 mm. Assume that each rivet is to carry one quarter of the load. If the shearing stress on the rivet is not to exceed 6.9×107Pa, the maximum tension that can be exerted by the riveted strip is
View SolutionA river 10m deep is flowing at 5ms−1. The shearing stress between the horizontal layers of the river is (η=10−(3)SI units)
View SolutionThe velocity of water in a rier is 18kmh−1 near the surface. If the river is 5 m deepm, find the shearing stress between the horizontal lyers of water. The coefficient of viscosity of water =10^-2 poise.
View Solution

