The radii and Young's moduli of two uniform wires A and B are in the ratio 2:1 and 1:2 respectively. Both wires are subjected to the same longitudinal force. If the increase in length of the wire A is one percent, the percentage increase in length of the wire B is
1.0
1.5
2.0
3.0
The correct Answer is:C
To solve the problem, we need to find the percentage increase in length of wire B given the percentage increase in length of wire A and the ratios of their radii and Young's moduli.
1. Identify Given Ratios:
- The ratio of the radii of wires A and B is given as rA:rB=2:1.
- The ratio of Young's moduli of wires A and B is given as YA:YB=1:2.
2. Express Radii and Young's Moduli:
- Let rB=r. Then rA=2r.
- Let YA=Y. Then YB=2Y.
3. Understand the Relationship of Length Increase:
- The increase in length ΔL of a wire under a longitudinal force F is given by the formula:
ΔLL=FA⋅Y
- Where A is the cross-sectional area of the wire. For a circular wire, A=πr2.
4. Relate the Increase in Length for Both Wires:
- For wire A:
ΔLALA=Fπ(r2A)YA=Fπ(4r2)Y=F4πr2Y
- For wire B:
ΔLBLB=Fπ(r2B)YB=Fπ(r2)(2Y)=F2πr2Y
5. Calculate the Ratio of Length Increases:
- The ratio of the percentage increases in lengths of wires A and B can be expressed as:
ΔLA/LAΔLB/LB=(F/(4πr2Y))(F/(2πr2Y))=24=12
6. Use the Given Percentage Increase in Length of Wire A:
- We are given that the percentage increase in length of wire A is 1%. Thus:
ΔLALA=0.01
- Therefore, using the ratio we found:
ΔLBLB=2×ΔLALA=2×0.01=0.02
7. Convert to Percentage:
- The percentage increase in length of wire B is:
ΔLB=0.02×100%=2%
Final Answer:
The percentage increase in length of wire B is 2%.
- The ratio of the radii of wires A and B is given as rA:rB=2:1.
- The ratio of Young's moduli of wires A and B is given as YA:YB=1:2.
- Let rB=r. Then rA=2r.
- Let YA=Y. Then YB=2Y.
- The increase in length ΔL of a wire under a longitudinal force F is given by the formula:
ΔLL=FA⋅Y
- Where A is the cross-sectional area of the wire. For a circular wire, A=πr2.
- For wire A:
ΔLALA=Fπ(r2A)YA=Fπ(4r2)Y=F4πr2Y
- For wire B:
ΔLBLB=Fπ(r2B)YB=Fπ(r2)(2Y)=F2πr2Y
- The ratio of the percentage increases in lengths of wires A and B can be expressed as:
ΔLA/LAΔLB/LB=(F/(4πr2Y))(F/(2πr2Y))=24=12
- We are given that the percentage increase in length of wire A is 1%. Thus:
ΔLALA=0.01
- Therefore, using the ratio we found:
ΔLBLB=2×ΔLALA=2×0.01=0.02
- The percentage increase in length of wire B is:
ΔLB=0.02×100%=2%
The percentage increase in length of wire B is 2%.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - APPLICATIONS OF ELASTIC BEHAVIOUR OF MATERIALS
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - HOTS
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - STRESS-STRAIN CURVE
5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT Exemplar
5 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A wire has Poisson's ratio 0.3. If the change in the length of the wire on stretching it is 1% then percentage change in the volume of the wire will be
View SolutionTwo parallel wires A and B are fixed to a right support at the upper ends and are subjected to the same load at the lower ends. The lengths of the wire are in the ratio 4:5 and their radius are in the ratio 4:3. The increase in length of the wire A is 1mm.Calculate the increase in length of the wire B.
View Solution
Knowledge Check
If the ratio of diameters,lengths and Young's moduli of steel and brass wires shown in the figure are p, q and r respectively . Then the corresponding ratio of increase in their lenghts would be
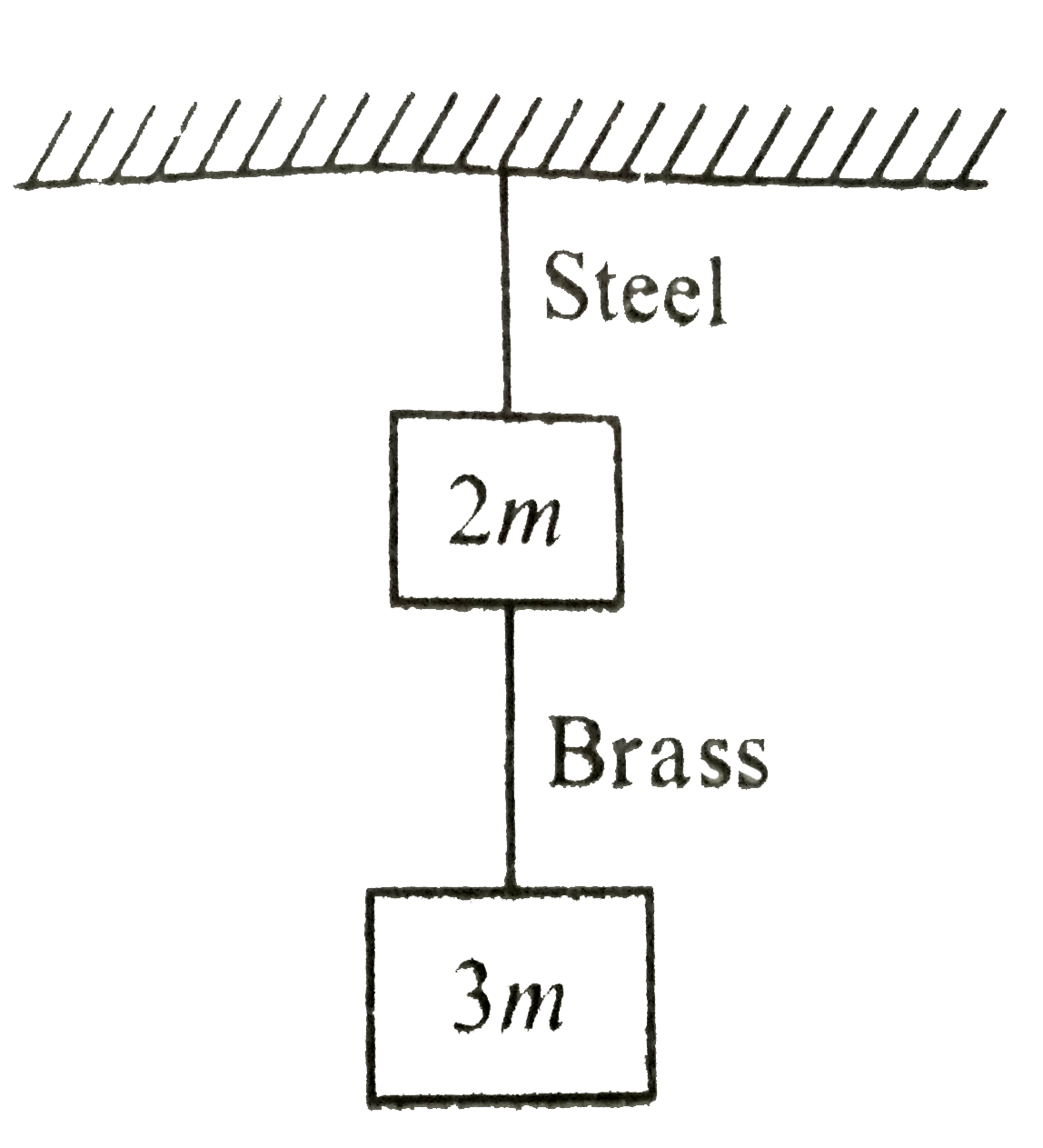 A3q5p2rB5q3p2rC3q5prD5q3pr
A3q5p2rB5q3p2rC3q5prD5q3pr
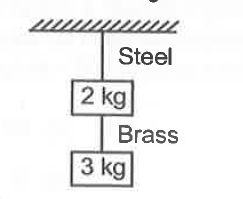
If the ratio of diameter, lengths and Young's moduli of steel and brass wires shown in figure are 2 : 1, 2 : 1 and 2 : 1 respectively, then the corresponding ratio of increase in their lengths would be
View SolutionA piece of copper wire has twice the radius of a piece of steel wire. Young's modulus for steel is twice that of the copper. One end of the copper wire is joined to one end of the steel wire so that both can be subjected to the same longitudinal force. By what fraction of its length will the steel have stretched when the length of the copper has increased by 1%?
View SolutionA piece of copper wire has twice the radius of a piece of steel wire. Young's modulus for steel is twice that of the copper. One end of the copper wire is joined to one end of the steel wire so that both can be subjected to the same longitudinal force. By what fraction of its length will the steel have stretched when the length of the copper has increased by 1%?
View SolutionThe wire is stretched to increase the length by 1%. Find the percentage change in the resistance.
View SolutionLongitudinal stress of 1kg/mm2 is applied on a wire. The percentage increase in length is (Y=1011N/m2)
View SolutionYoung's moduli of two wires A and B are in the ratio 7:4 wire A is 2m long and has radius R. . wire B is 1.5mlong has radius 2mm for a given load , then the value of R is close to:
View SolutionIf the ratio of lengths, radii and Young's moduli of steel and brass wires in the figure are a,b and c respectively then the corresponding ratio of increase in their lengths is
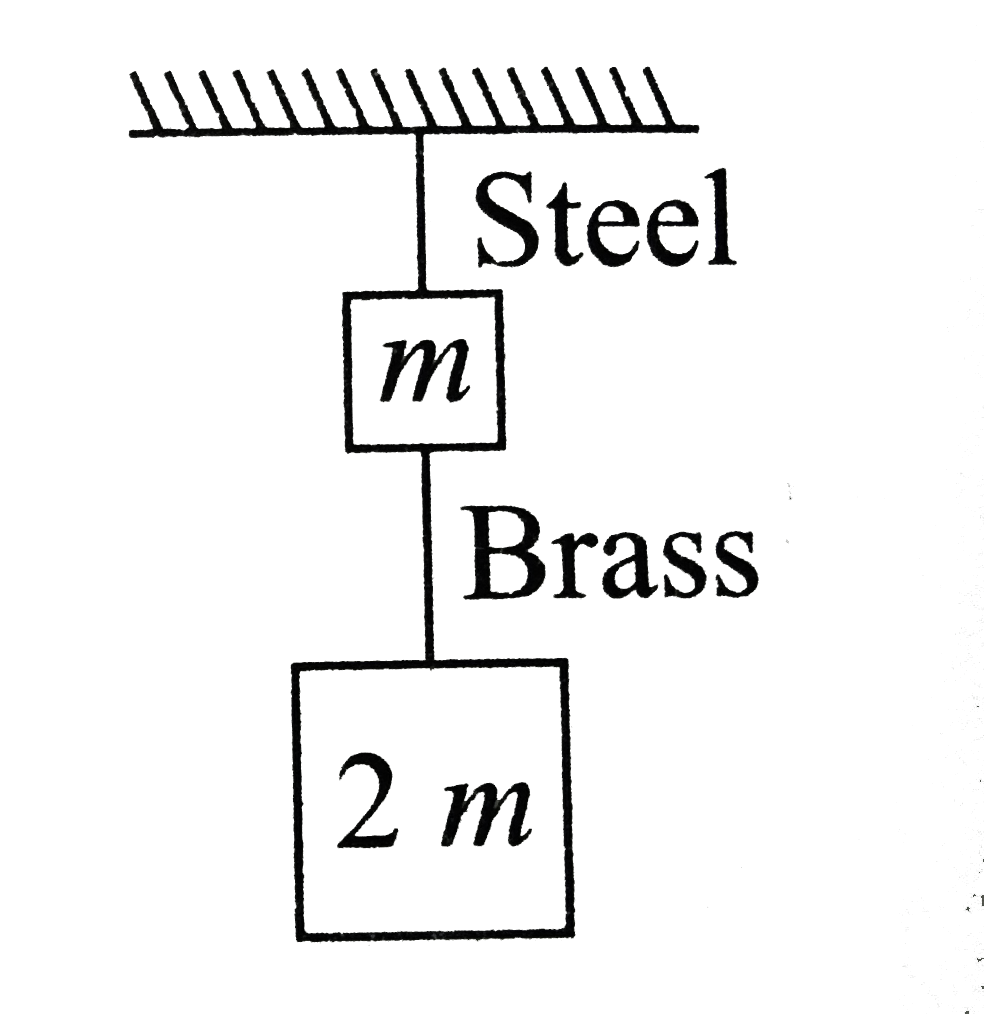
View Solution
