If the displacement-time graph for a particle is parallel to time-axis, how much is the velocity of the particle ?
To determine the velocity of a particle when its displacement-time graph is parallel to the time-axis, we can follow these steps:
1. Understanding the Displacement-Time Graph:
- A displacement-time graph shows how the displacement of a particle changes over time. If the graph is parallel to the time-axis, it indicates that the displacement remains constant over time.
2. Identifying the Slope:
- The slope of a displacement-time graph represents the velocity of the particle. Mathematically, the slope is calculated as:
slope=ΔyΔx
where Δy is the change in displacement and Δx is the change in time.
3. Analyzing the Parallel Line:
- Since the graph is parallel to the time-axis, the change in displacement (Δy) is zero. This means:
Δy=0
4. Calculating the Velocity:
- Substituting Δy=0 into the slope formula gives:
slope=0Δx=0
- Therefore, the velocity of the particle is:
velocity=0
5. Conclusion:
- The particle is not moving, as indicated by the zero velocity.
Final Answer:
The velocity of the particle is 0 m/s.
---
- A displacement-time graph shows how the displacement of a particle changes over time. If the graph is parallel to the time-axis, it indicates that the displacement remains constant over time.
- The slope of a displacement-time graph represents the velocity of the particle. Mathematically, the slope is calculated as:
slope=ΔyΔx
where Δy is the change in displacement and Δx is the change in time.
- Since the graph is parallel to the time-axis, the change in displacement (Δy) is zero. This means:
Δy=0
- Substituting Δy=0 into the slope formula gives:
slope=0Δx=0
- Therefore, the velocity of the particle is:
velocity=0
- The particle is not moving, as indicated by the zero velocity.
The velocity of the particle is 0 m/s.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the time-displacement graph of a particle is parallel to the-axis, the velocity of the particle is
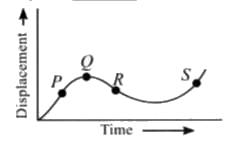
AinfinityBunityCequal to accleration of the bodyDzeroThe displacement-time graph of a moving particle is shown below. The instantaneous velocity of the particle is negative at the point
ACBDCEDFThe displacement-time graph of a moving particle is shown below. The instantaneous velocity of the particle is negative at the point
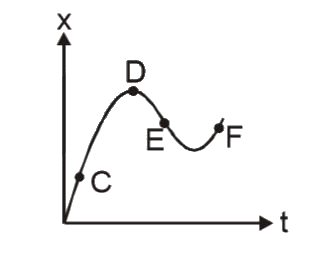 ACBDCEDF
ACBDCEDF
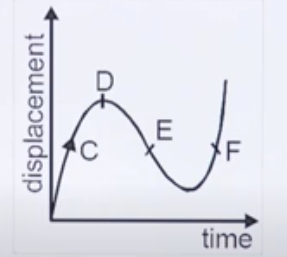
The displacement time graph of a moving particle is shown below
The instantaneous velocity of the particle is negative at the point
View SolutionIf the displacement-time graph of a body is a straight line parallel to the time axis, what is the nature of motion of the body?
View SolutionFigure shows the displacement time graph of a particle moving on the X-axis

View SolutionFigure show the displacement - time graph of a particle moving on the x-axis
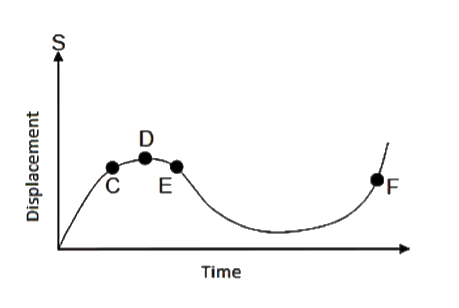
View SolutionThe displacement-time graph of moving particle is shown below

The instantaneous velocity of the particle in negative at the point
View Solution