Derive the equations of motion given below: v=u+at
To derive the equation of motion v=u+at, we start with the basic definitions of motion under uniform acceleration.
Step 1: Understand the Definitions
- Let u be the initial velocity of the object.
- Let v be the final velocity of the object after time t.
- Let a be the constant acceleration.
- The acceleration a is defined as the rate of change of velocity with respect to time.
Step 2: Write the Definition of Acceleration
From the definition of acceleration, we have:
a=dvdt
This means that the change in velocity dv over a small time interval dt is equal to the acceleration.
Step 3: Rearranging the Equation
We can rearrange the equation to express dv:
dv=adt
Step 4: Integrate Both Sides
Now, we will integrate both sides. The left side will be integrated with respect to velocity from the initial velocity u to the final velocity v, and the right side will be integrated with respect to time from 0 to t:
∫vudv=∫t0adt
Step 5: Calculate the Integrals
The left side integrates to:
v−u
The right side integrates to:
at
Thus, we have:
v−u=at
Step 6: Rearranging to Find the Final Equation
Now, rearranging this equation gives us the desired result:
v=u+at
Conclusion
We have derived the equation of motion v=u+at.
---
- Let u be the initial velocity of the object.
- Let v be the final velocity of the object after time t.
- Let a be the constant acceleration.
- The acceleration a is defined as the rate of change of velocity with respect to time.
From the definition of acceleration, we have:
a=dvdt
This means that the change in velocity dv over a small time interval dt is equal to the acceleration.
We can rearrange the equation to express dv:
dv=adt
Now, we will integrate both sides. The left side will be integrated with respect to velocity from the initial velocity u to the final velocity v, and the right side will be integrated with respect to time from 0 to t:
∫vudv=∫t0adt
The left side integrates to:
v−u
The right side integrates to:
at
Thus, we have:
v−u=at
Now, rearranging this equation gives us the desired result:
v=u+at
We have derived the equation of motion v=u+at.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The equation of motion may be given by
Ax=±Asin(√ba)tBx=±Acos(√ba)tCx=±Asin(√bat+θ) where θ=π2DNone of the above.The equation of the graph given below is
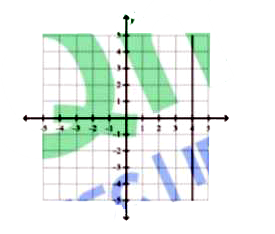 AY=4BX=4CX=−4DY=0
AY=4BX=4CX=−4DY=0An object is moving with uniform acceleration a. Its initial velocity is u and after time t its velocity is v. The equation of its motion is v = u + at. The velocity (along y-axis) time (along x-axis) graph shall be a straight line
Apassing through originBwith x-intercept uCwith y-intercept uDwith slope u
For uniform accelerated motion, draw by graphical method establish the following equations of motion : v = u + at
View SolutionDerive the following equations of motion for an object moving with constant acceleration along a straight line : snth=v0+a2(2n−1).
View SolutionDerive the following equations of motion for an object moving with constant acceleration along a straight line : v2=v20+2a(x−x0)=v20+2as
View SolutionDerive the following equations of motion for uniformly accelerated motion from velocity-time graph : s=ut+12at2
View SolutionWrite and derive all the three equations of motion analytically.
View Solution

