What is the area under the velocity-time curve in the case of a body projected vertically upwards from the ground after reaching the ground ?
To solve the problem of finding the area under the velocity-time curve for a body projected vertically upwards from the ground after it has reached the ground, we can follow these steps:
Step 1: Understand the motion of the body
When a body is projected vertically upwards with an initial velocity u, it will rise until it reaches its maximum height, at which point its velocity becomes zero. After reaching the maximum height, the body will fall back down to the ground.
Step 2: Analyze the velocity-time graph
The velocity of the body changes as follows:
- From the time of projection until it reaches the maximum height, the velocity decreases from u to 0.
- After reaching the maximum height, the velocity becomes negative as the body falls back down, increasing in magnitude until it reaches the ground.
Step 3: Determine the time taken for ascent and descent
The time taken to reach the maximum height can be calculated using the formula:
tup=ug
where g is the acceleration due to gravity. The time taken to descend back to the ground is the same, so:
tdown=ug
Step 4: Sketch the velocity-time graph
1. The graph will start at (0,u) and decrease linearly to (tup,0).
2. After that, it will drop to (tup+tdown,−u).
3. The area above the time axis (during ascent) is positive, while the area below the time axis (during descent) is negative.
Step 5: Calculate the areas
- The area under the curve during the ascent (from 0 to tup) is a triangle:
Areaup=12×base×height=12×ug×u=u22g
- The area under the curve during the descent (from tup to tup+tdown) is also a triangle:
Areadown=−12×base×height=−12×ug×u=−u22g
Step 6: Find the total area
To find the total area under the velocity-time curve, we add the areas from both the ascent and descent:
Total Area=Areaup+Areadown
Total Area=u22g−u22g=0
Conclusion
The area under the velocity-time curve for a body projected vertically upwards from the ground after it has reached the ground is zero.
---
When a body is projected vertically upwards with an initial velocity u, it will rise until it reaches its maximum height, at which point its velocity becomes zero. After reaching the maximum height, the body will fall back down to the ground.
The velocity of the body changes as follows:
- From the time of projection until it reaches the maximum height, the velocity decreases from u to 0.
- After reaching the maximum height, the velocity becomes negative as the body falls back down, increasing in magnitude until it reaches the ground.
The time taken to reach the maximum height can be calculated using the formula:
tup=ug
where g is the acceleration due to gravity. The time taken to descend back to the ground is the same, so:
tdown=ug
1. The graph will start at (0,u) and decrease linearly to (tup,0).
2. After that, it will drop to (tup+tdown,−u).
3. The area above the time axis (during ascent) is positive, while the area below the time axis (during descent) is negative.
- The area under the curve during the ascent (from 0 to tup) is a triangle:
Areaup=12×base×height=12×ug×u=u22g
Areadown=−12×base×height=−12×ug×u=−u22g
To find the total area under the velocity-time curve, we add the areas from both the ascent and descent:
Total Area=Areaup+Areadown
Total Area=u22g−u22g=0
The area under the velocity-time curve for a body projected vertically upwards from the ground after it has reached the ground is zero.
Topper's Solved these Questions
Similar Questions
Indicate the velocity (v) - time (t) graphs for a body:
(i) falling under gravity.
(ii) thrown vertically upwards till it falls back to the ground after reaching the highest point.
View SolutionA stone is dropped from the top of a 400m high tower. At the same time another stone is projected vertically upwards from the ground with a speed of 50m/s. The two stones will cross each other after a time
View Solution
Knowledge Check
Velocity-time curve for a body projected vertically upwards is
AParabolaBEllipseCHyperbolaDStraight lineA body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A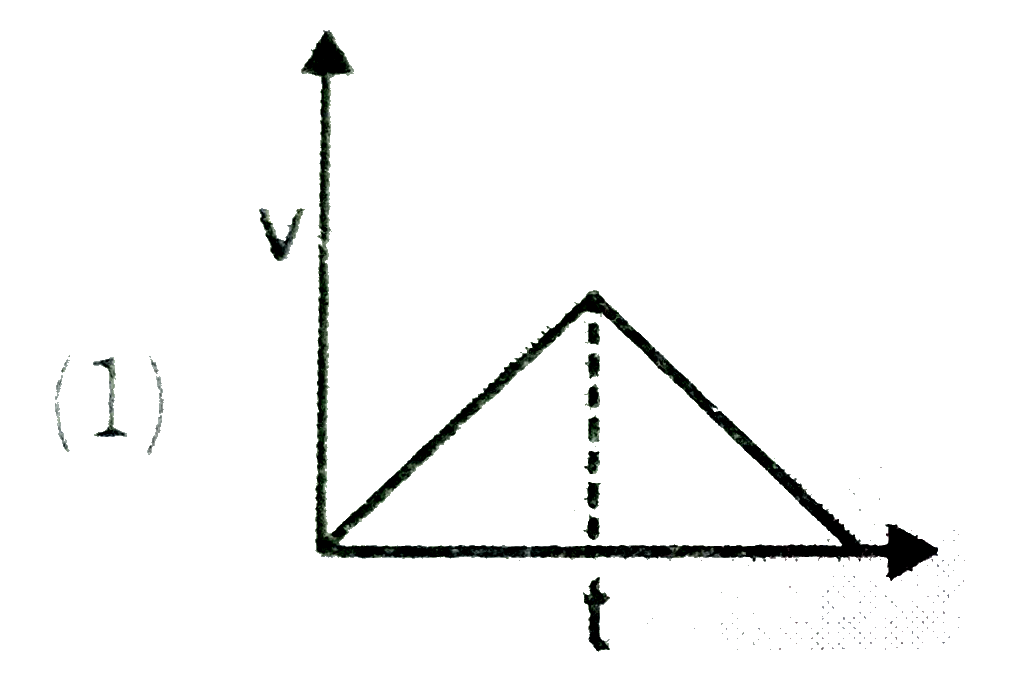 B
B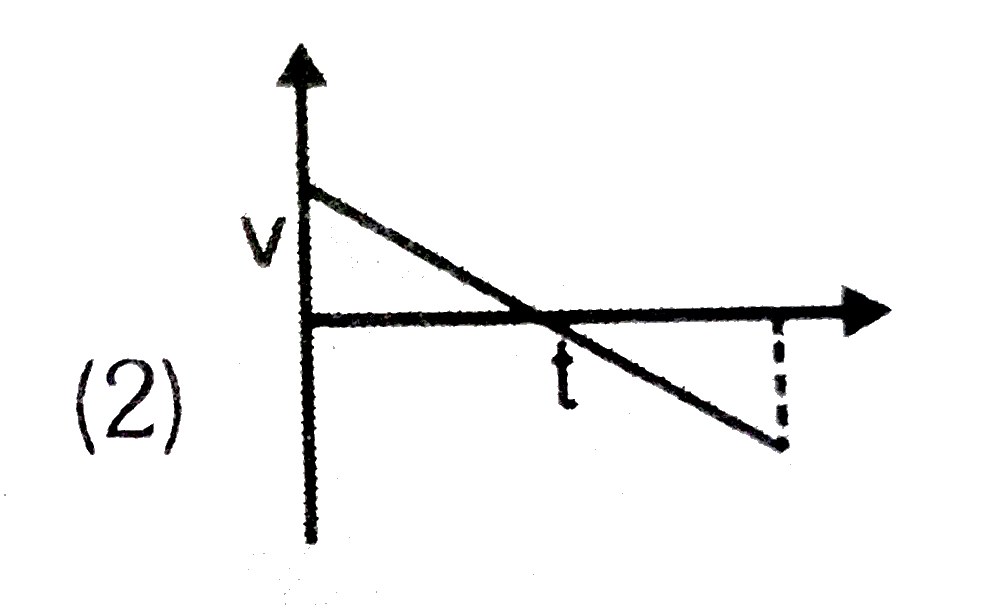 C
C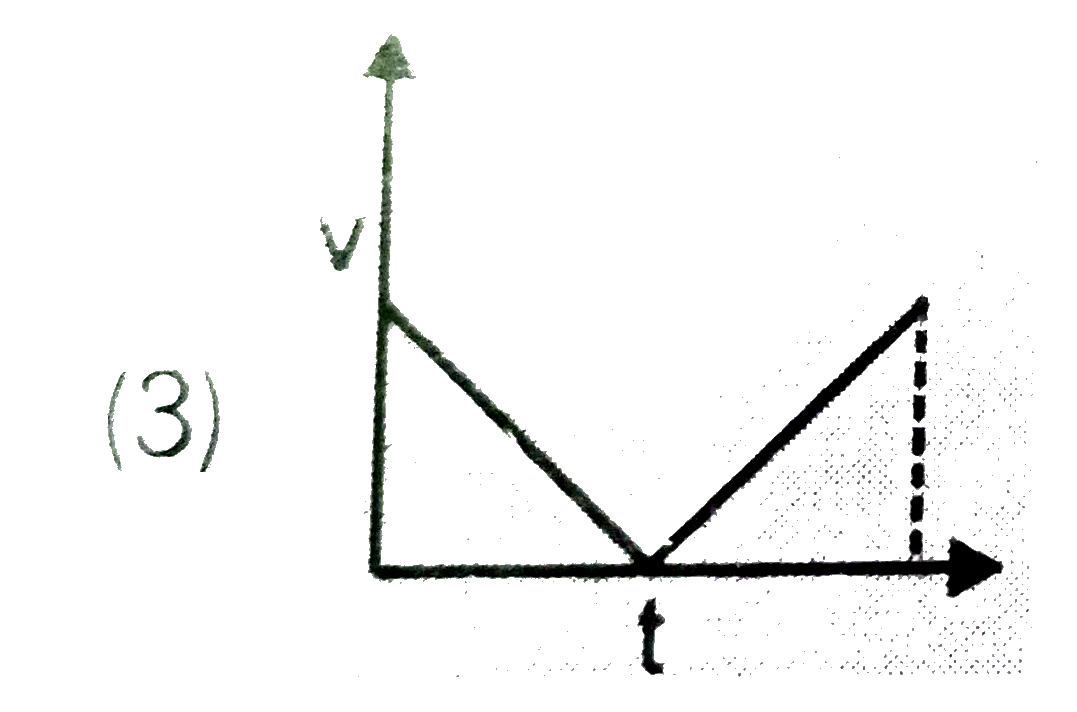 D
D
Two bodies are projected simultaneously with the same velocity of 19.6m/s from the top of a tower one vertically upwards and the other vertically downwards. As they reach the ground, the time gap is
A0 sB2 sC4 sD6 s
Two particles A and B having different masses arc projected from a tower with same speed. A is projected vertically upward and B vertically downward. On reaching the ground
View SolutionThe velocity time graph for the veticaly component of the velocity of a body thrown upwards from the ground and landing on the roof of a building is given in the figure.The height of the building is:
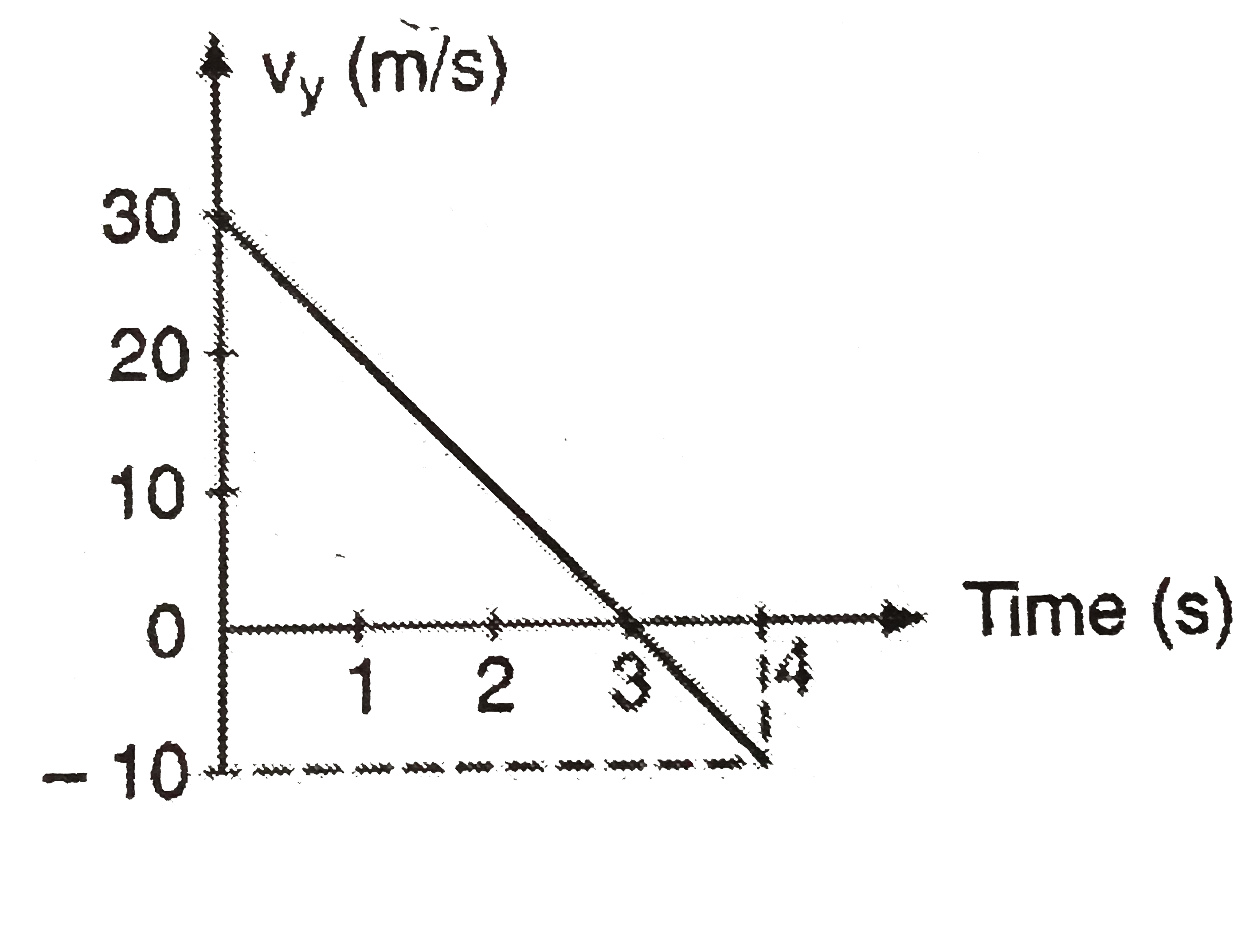
View SolutionThe escape velocity for a body projected vertically upwards from the surface of earth is 11km/s. If the body is projected at an angle of 45∘ with the vertical, the escape velocity will be
View SolutionThe escape velocity for a body projected vertically upwards from the surface of earth is 11km/s. If the body is projected at an angle of 45∘ with the vertical, the escape velocity will be
View SolutionFrom certain height h two bodies are projected horizontally each with velocity v.One body is projected towards North and the other body is projected towards east. Their separation on reaching the ground
View Solution

