The v-t graphs of two objects make angles of and with the time-axis. Find the ratio of their accelerations.
To find the ratio of the accelerations of two objects based on their velocity-time (v-t) graphs making angles of 30∘ and 60∘ with the time-axis, we can follow these steps:
1. Understand the v-t Graphs:
- The v-t graph represents the relationship between velocity (v) and time (t).
- The slope of the v-t graph gives the acceleration (a) of the object.
2. Identify the Angles:
- For the first object, the v-t graph makes an angle of 30∘ with the time-axis.
- For the second object, the v-t graph makes an angle of 60∘ with the time-axis.
3. Calculate the Slopes:
- The slope of the graph can be determined using the tangent of the angle it makes with the time-axis.
- For the first object (angle 30∘):
a1=tan(30∘)=1√3
- For the second object (angle 60∘):
a2=tan(60∘)=√3
4. Find the Ratio of Accelerations:
- The ratio of the accelerations a1 to a2 is given by:
a1a2=tan(30∘)tan(60∘)=1√3√3
- Simplifying this gives:
a1a2=1√3⋅1√3=13
5. Express the Ratio:
- Therefore, the ratio of the accelerations a1:a2 is:
a1:a2=1:3
Final Answer:
The ratio of the accelerations of the two objects is 1:3.
- The v-t graph represents the relationship between velocity (v) and time (t).
- The slope of the v-t graph gives the acceleration (a) of the object.
- For the first object, the v-t graph makes an angle of 30∘ with the time-axis.
- For the second object, the v-t graph makes an angle of 60∘ with the time-axis.
- The slope of the graph can be determined using the tangent of the angle it makes with the time-axis.
- For the first object (angle 30∘):
a1=tan(30∘)=1√3
- For the second object (angle 60∘):
a2=tan(60∘)=√3
- The ratio of the accelerations a1 to a2 is given by:
a1a2=tan(30∘)tan(60∘)=1√3√3
- Simplifying this gives:
a1a2=1√3⋅1√3=13
- Therefore, the ratio of the accelerations a1:a2 is:
a1:a2=1:3
The ratio of the accelerations of the two objects is 1:3.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In displacement time graph, two straight lines make angles 60∘and30∘ with time axis. The ratio of mangnitudes of the velocities represented by them is
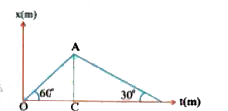 A1:2B1:3C2:1D3:1
A1:2B1:3C2:1D3:1The displacement-time graph for two particle A and B straight lines inclined at angle of 30∘ and 90∘ with the time axis. The ratio of the velocities VA and VB is :
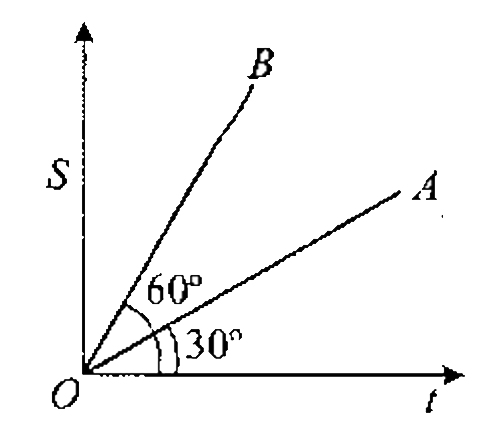 A1:2B1:√3C√3:1D1:3
A1:2B1:√3C√3:1D1:3The displacement-time graph for two particles A and B are straight lines inclined at angles of 30∘ and 60∘ with the time axis. The ratio of velocities of VA:VB is
A1:2B1:√3C√3:1D1:3
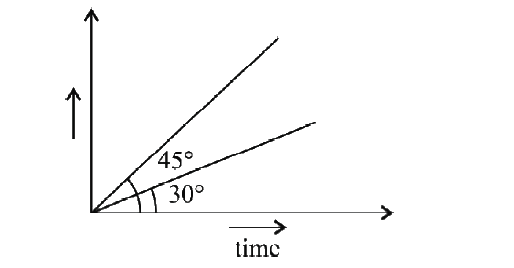
Completion type Question : The displacement time graphs for two particles A and B are straight lines inclined at angles of 30∘ and 45∘ with the time axis. The ratio of their velocities vA:vB = ………..
View SolutionThe displacemenet time graph of two moving particles make agnes of 30∘and45∘ with the x-axis. The ratio of the two velocities VAandVB is
View SolutionAn unpolarized light passes through three polarizing sheets whose polarizing directions make an angle of 30∘, 60∘ and 30∘ with y axis in same sense. The tion of initial-intensity is transmitted by the system is k32. Find k.
View SolutionThe displacement-time graph for two particles A and B are straight lines inclined at angles of 30∘ and 60∘ with the time axis. The ratio of velocities of VA:VB is
View SolutionThe displacement-time graph for two particle A and B are straight lines inclined at angles of 45∘and 60∘ with the time axis. The ratio of velocities of vA and vB is
View Solution
