Completion type Question : The displacement time graphs for two particles A and B are straight lines inclined at angles of 30∘ and 45∘ with the time axis. The ratio of their velocities vA:vB = ………..
To find the ratio of the velocities vA:vB for the two particles A and B based on their displacement-time graphs, we can follow these steps:
Step 1: Understand the relationship between slope and velocity
The slope of a displacement-time graph represents the velocity of the particle. Therefore, if we have a straight line graph, the slope can be calculated using the angle of inclination with respect to the time axis.
Step 2: Identify the angles
For particle A, the angle of inclination with the time axis is 30∘. For particle B, the angle of inclination is 45∘.
Step 3: Use the tangent function to find the slopes
The slope of the graph (which represents velocity) can be expressed in terms of the tangent of the angle:
- For particle A:
vA=tan(30∘)
- For particle B:
vB=tan(45∘)
Step 4: Calculate the values of the tangents
Using known values:
- tan(30∘)=1√3
- tan(45∘)=1
Step 5: Set up the ratio of the velocities
Now we can express the ratio of the velocities:
vAvB=tan(30∘)tan(45∘)=1√31
Step 6: Simplify the ratio
This simplifies to:
vAvB=1√3
Step 7: Express the ratio in the required format
Thus, the ratio of the velocities vA:vB can be expressed as:
vA:vB=1:√3
Final Answer
The ratio of their velocities vA:vB=1:√3.
---
The slope of a displacement-time graph represents the velocity of the particle. Therefore, if we have a straight line graph, the slope can be calculated using the angle of inclination with respect to the time axis.
For particle A, the angle of inclination with the time axis is 30∘. For particle B, the angle of inclination is 45∘.
The slope of the graph (which represents velocity) can be expressed in terms of the tangent of the angle:
- For particle A:
vA=tan(30∘)
- For particle B:
vB=tan(45∘)
Using known values:
- tan(30∘)=1√3
- tan(45∘)=1
Now we can express the ratio of the velocities:
vAvB=tan(30∘)tan(45∘)=1√31
This simplifies to:
vAvB=1√3
Thus, the ratio of the velocities vA:vB can be expressed as:
vA:vB=1:√3
The ratio of their velocities vA:vB=1:√3.
Topper's Solved these Questions
Similar Questions
The displacement-time graph of two particles A and B are straight line making angle of 60∘ and 45∘ with x-axis respectively. Then find the ratio of velocity of A and velocity of B.
View SolutionThe displacement time graph for two particles AandB are straight lines inclined at 30∘ with time axis and at 30∘ to displacement axis respectively. Calcualte ratio of velocities of the two particles.
View Solution
Knowledge Check
The displacement-time graph for two particles A and B are straight lines inclined at angles of 30∘ and 60∘ with the time axis. The ratio of velocities of VA:VB is
A1:2B1:√3C√3:1D1:3The displacement-time graph for two particle A and B are straight lines inclined at angles of 45∘and 60∘ with the time axis. The ratio of velocities of vA and vB is
A1:2B1:√3C√3:1D2:1The displacement-time graph for two particle A and B straight lines inclined at angle of 30∘ and 90∘ with the time axis. The ratio of the velocities VA and VB is :
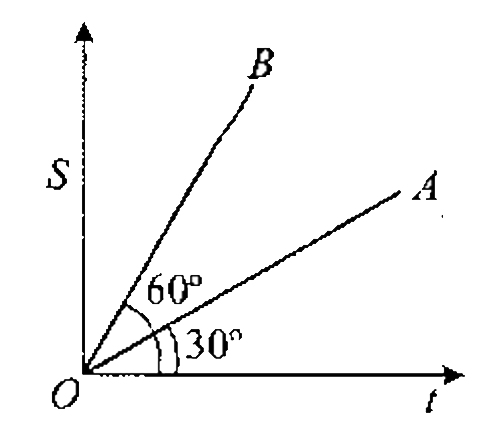 A1:2B1:√3C√3:1D1:3
A1:2B1:√3C√3:1D1:3
The v-t graphs of two objects make angles of 30∘ and 60∘ with the time-axis. Find the ratio of their accelerations.
View SolutionThe displacement-time graph for two particles is as shown. Find the ratio of their velocities.
View SolutionThe displacement-time graph for two particles A and B are straight lines inclined at angles of 30∘ and 60∘ with the time axis. The ratio of velocities of VA:VB is
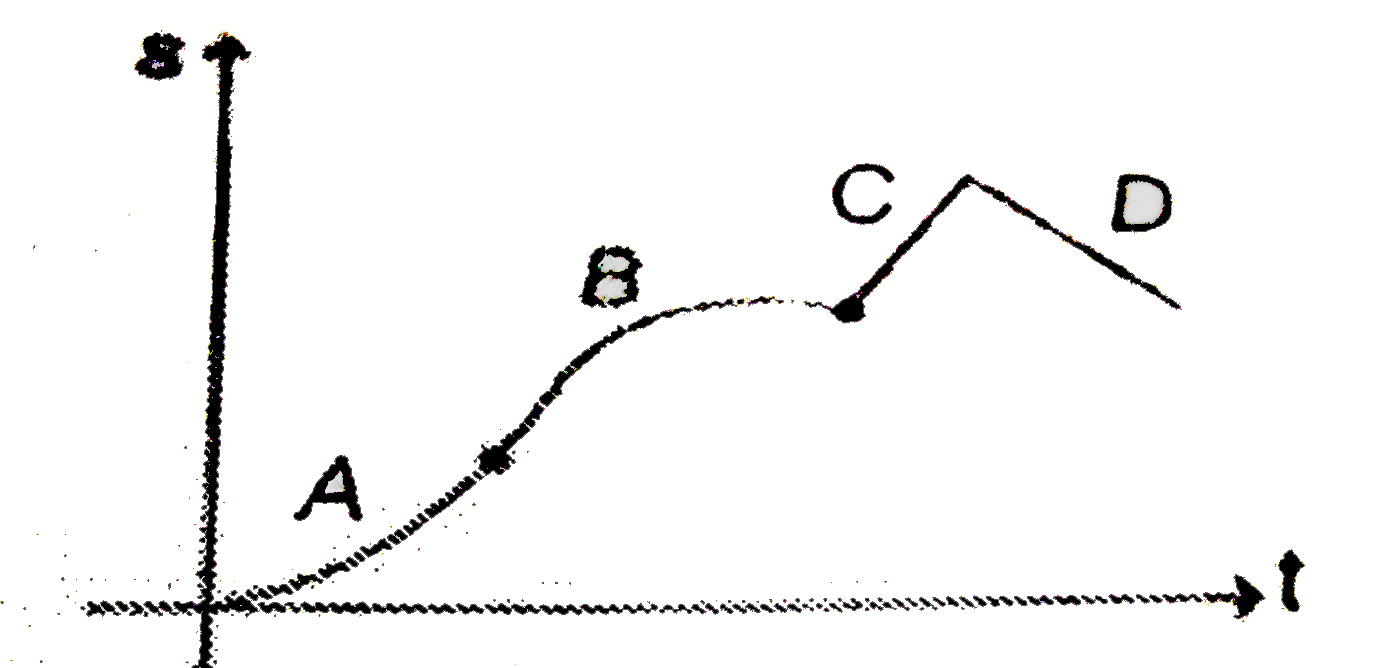
View SolutionDisplacement time graph of a particle moving in a straight line is a shown in figure.
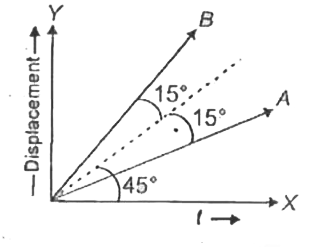
View SolutionThe displacement - time graph for two particles A and B is as follows. The ratio vAvB is
View Solution

