For a closed container containing 100 mol of an ideal gas fitted with movable, frictionless, weightless piston operating such that pressure of gas remain constant at 8.21 atm, which graph repsents correct variation of log Vv/s log T where V is in litre and T is in Kelvin ? (R=0.0821atmLmolK)

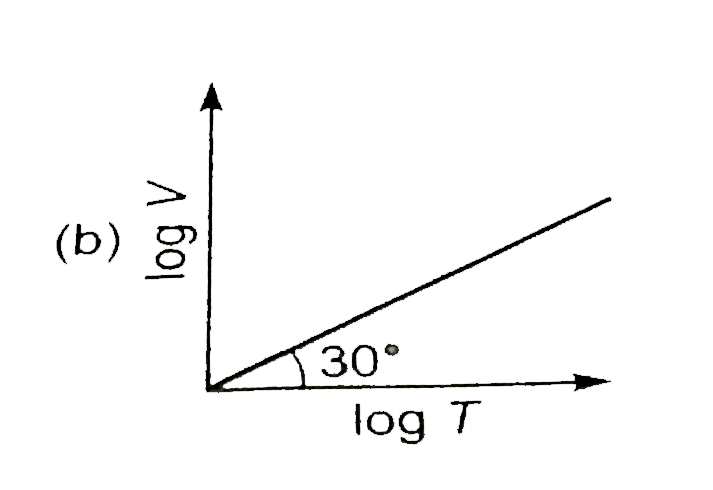

The correct Answer is:A
To solve the problem, we need to analyze the relationship between the volume (V) and temperature (T) of an ideal gas under constant pressure conditions. We will use the ideal gas law and logarithmic properties to derive the relationship.
1. Identify the Given Values:
- Number of moles (n) = 100 mol
- Pressure (P) = 8.21 atm
- Gas constant (R) = 0.0821 (atm·L)/(mol·K)
2. Use the Ideal Gas Law:
The ideal gas law is given by:
PV=nRT
Rearranging this equation for volume (V):
V=nRTP
3. Substituting the Known Values:
Substitute the known values into the equation:
V=100mol×0.0821atm⋅Lmol⋅K×T8.21atm
Simplifying this gives:
V=100×0.0821×T8.21
4. Calculate the Constant:
Calculate the constant factor:
V=8.218.21×100×0.0821×T=100×0.010×T=0.821×T
5. Taking Logarithm:
Now, take the logarithm of both sides:
logV=log(0.821×T)
Using the logarithmic property log(ab)=loga+logb:
logV=log0.821+logT
6. Rearranging the Equation:
Rearranging gives:
logV=logT+log0.821
This indicates a linear relationship between logV and logT.
7. Graph Interpretation:
The graph of logV vs. logT will be a straight line with a slope of 1, indicating that as temperature increases, volume also increases at a constant pressure.
Conclusion:
The correct graph representing the variation of logV vs. logT is a straight line with a positive slope.
- Number of moles (n) = 100 mol
- Pressure (P) = 8.21 atm
- Gas constant (R) = 0.0821 (atm·L)/(mol·K)
The ideal gas law is given by:
PV=nRT
Rearranging this equation for volume (V):
V=nRTP
Substitute the known values into the equation:
V=100mol×0.0821atm⋅Lmol⋅K×T8.21atm
Simplifying this gives:
V=100×0.0821×T8.21
Calculate the constant factor:
V=8.218.21×100×0.0821×T=100×0.010×T=0.821×T
Now, take the logarithm of both sides:
logV=log(0.821×T)
Using the logarithmic property log(ab)=loga+logb:
logV=log0.821+logT
Rearranging gives:
logV=logT+log0.821
This indicates a linear relationship between logV and logT.
The graph of logV vs. logT will be a straight line with a slope of 1, indicating that as temperature increases, volume also increases at a constant pressure.
The correct graph representing the variation of logV vs. logT is a straight line with a positive slope.
Topper's Solved these Questions
- THERMODYNAMICSBook:NARENDRA AWASTHI ENGLISHChapter:THERMODYNAMICSExercise:Level 2
Explore 40 Videos
- THERMODYNAMICSBook:NARENDRA AWASTHI ENGLISHChapter:THERMODYNAMICSExercise:Level 3
Explore 89 Videos
- STOICHIOMETRYBook:NARENDRA AWASTHI ENGLISHChapter:STOICHIOMETRYExercise:Match the Colum-II
Explore 6 Videos
Similar Questions
Ten moles of an ideal gas are filled in a closed vessel. The vessel has cylinder and piston type arrangement and pressure of the gas remains constant at 0.821 atm. Which of the following graph represents correct variation of log V vs log T?
(V = Volume in litre and T = temperature in Kelvin)
View SolutionFor a closed container containing 10 moles of an ideal gas, at constant pressure of 0.82 atm, which graph correctly represent, variation of log V us log T where volume is in litre and temp. in kelvin :
View Solution3 moles of an ideal gas are contained within a cylinder by a frictionless piston and are initially at temperature T . The pressure of the gas remains constant while it is heated and its volume doubles . If R is molar gas constant , the work done by the gas in increasing its volume is
View SolutionIn a closed rigid container an ideal gas is filled. If the gas is heated, the graph of pressure (P) v/s root mean square speed (rms) will be :
View SolutionV vs T curves at constant pressure P1 and P2 for an ideal gas are shown below
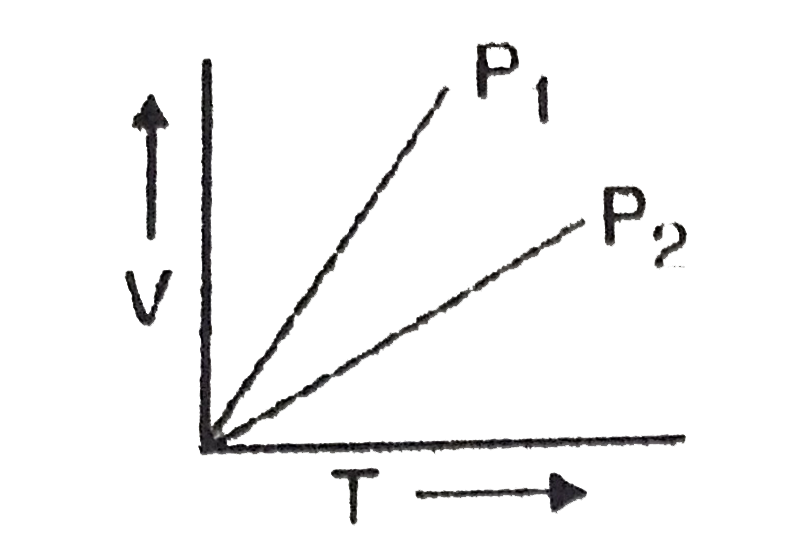
Which is correct ?
View SolutionTwo moles of an ideal gas is contained in a cylinder fitted with a frictionless movable piston, exposed to the atmosphere, at an initial temperature T0. The gas is slowly heated so that its volume becomes four times the initial value. The work done by gas is
View SolutionV vs T curves at constant pressure P1 and P2 for an ideal gas are shown in the figure. Which of the following is correct?

View SolutionA vertical thermally insulated cylinder of volume V contain n moles of an ideal monoatomic gas under a weightless piston. A load of weight W is placed on the piston as a result of which the piston is displaced. If the initial temp of the gas is 300K, area of piston is A and atmospheric pressure P0. (take W=P0A). Determine the value of final temperature of the gas
View SolutionThe slope of 'P' v/s T plot at constant volume for a fixed amount of an ideal gas aus 0.01atm/K. Then what will be the value of pressure of gas (In atm) at 300K temperature ?
View SolutionHeart leaks into a vessel, containing one mole of an ideal monoatomic gas at a constant rate of R4s−1 where R is universal gas constatant. It is observed that the gas expands at a constant rate dVdt=V0400(second) where V0 is intial volume. The inital temperature is given by T0=40K. What will be final temperature of gas at time t=400s.
View Solution

