If the boundary of system moves by an infinitesimal amount, the work involved is given by dw=−PextdV
for irreversible process w=−PextΔV (where ΔV=Vf−Vi)
for reversible process Pext=Pint±dP≅Pint
so for reversible isothermal process w=−nRTln.VfVi
2mole of an ideal gas undergoes isothermal compression along three different plaths :
(i) reversible compression from Pi=2 bar and Vi=8L to Pf=20 bar
(ii) a single stage compression against a constant external pressure of 20 bar, and
(iii) a two stage compression consisting initially of compression against a constant external pressure of 10 bar until Pgas=Pext, followed by compression against a constant pressure of 20 bar until Pgas=Pext
Total work done on the gas in two stage compression is :
40
80
160
None of these
The correct Answer is:B
To solve the problem of calculating the total work done on the gas during a two-stage compression process, we will follow these steps systematically:
Step 1: Identify the Initial Conditions
We have 2 moles of an ideal gas undergoing isothermal compression. The initial conditions are:
- Initial Pressure, Pi=2 bar
- Initial Volume, Vi=8 L
Step 2: Calculate Initial Work Done in the First Stage
In the first stage, the gas is compressed against a constant external pressure of Pext=10 bar until the gas pressure equals the external pressure.
Using the formula for work done during compression:
w=−PextΔV
where ΔV=Vf−Vi.
To find Vf when Pgas=Pext:
Using the ideal gas law:
PV=nRT
At the end of the first stage:
Pext⋅Vf=nRT
Substituting Pext=10 bar, n=2 moles, and R=0.0831L⋅bar/(K⋅mol) (assuming isothermal conditions at a constant temperature T):
Vf=nRTPext=2⋅0.0831⋅T10
Now, we need to find T:
Using the initial conditions:
Pi⋅Vi=nRT⟹T=Pi⋅VinR=2⋅82⋅0.0831=160.1662≈96.3K
Now substituting T back into the equation for Vf:
Vf=2⋅0.0831⋅96.310≈1.60L
Now, calculate the work done in the first stage:
ΔV=Vf−Vi=1.60−8=−6.4L
w1=−10⋅(−6.4)=64L⋅bar
Step 3: Calculate Work Done in the Second Stage
In the second stage, the gas is compressed against a constant external pressure of Pext=20 bar until the gas pressure equals the external pressure.
Using the same formula:
w2=−PextΔV
Now, we need to find the new volume Vf when Pgas=20 bar:
Vf=nRTPext=2⋅0.0831⋅96.320≈0.83L
Now calculate the work done in the second stage:
ΔV=Vf−Vf(from first stage)=0.83−1.60=−0.77L
w2=−20⋅(−0.77)=15.4L⋅bar
Step 4: Total Work Done
The total work done on the gas during the two-stage compression is:
Wtotal=w1+w2=64+15.4=79.4L⋅bar
Final Answer
The total work done on the gas in the two-stage compression is approximately 79.4 L·bar.
We have 2 moles of an ideal gas undergoing isothermal compression. The initial conditions are:
- Initial Pressure, Pi=2 bar
- Initial Volume, Vi=8 L
In the first stage, the gas is compressed against a constant external pressure of Pext=10 bar until the gas pressure equals the external pressure.
w=−PextΔV
where ΔV=Vf−Vi.
Using the ideal gas law:
PV=nRT
At the end of the first stage:
Pext⋅Vf=nRT
Substituting Pext=10 bar, n=2 moles, and R=0.0831L⋅bar/(K⋅mol) (assuming isothermal conditions at a constant temperature T):
Vf=nRTPext=2⋅0.0831⋅T10
Using the initial conditions:
Pi⋅Vi=nRT⟹T=Pi⋅VinR=2⋅82⋅0.0831=160.1662≈96.3K
Vf=2⋅0.0831⋅96.310≈1.60L
ΔV=Vf−Vi=1.60−8=−6.4L
w1=−10⋅(−6.4)=64L⋅bar
In the second stage, the gas is compressed against a constant external pressure of Pext=20 bar until the gas pressure equals the external pressure.
w2=−PextΔV
Now, we need to find the new volume Vf when Pgas=20 bar:
Vf=nRTPext=2⋅0.0831⋅96.320≈0.83L
ΔV=Vf−Vf(from first stage)=0.83−1.60=−0.77L
w2=−20⋅(−0.77)=15.4L⋅bar
The total work done on the gas during the two-stage compression is:
Wtotal=w1+w2=64+15.4=79.4L⋅bar
The total work done on the gas in the two-stage compression is approximately 79.4 L·bar.
Topper's Solved these Questions
Similar Questions
If the boundary of system moves by an infinitesimal amount, the work involved is given by dw=−PextdV
for irreversible process w=−PextΔV (where ΔV=Vf−Vi)
for reversible process Pext=Pint±dP≅Pint
so for reversible isothermal process w=−nRTln.VfVi
2mole of an ideal gas undergoes isothermal compression along three different paths :
(i) reversible compression from Pi=2 bar and Vi=8L to Pf=20 bar
(ii) a single stage compression against a constant external pressure of 20 bar, and
(iii) a two stage compression consisting initially of compression against a constant external pressure of 10 bar until Pgas=Pext, followed by compression against a constant pressure of 20 bar until Pgas=Pext
Order of magnitude of work is :
View SolutionIf the boundary of system moves by an infinitesimal amount, the work involved is given by dw=−PextdV
for irreversible process w=−PextΔV (where ΔV=Vf−Vi)
for reversible process Pext=Pint±dP≅Pint
so for reversible isothermal process w=−nRTln.VfVi
2mole of an ideal gas undergoes isothermal compression along three different plaths :
(i) reversible compression from Pi=2 bar and Vi=8L to Pf=20 bar
(ii) a single stage compression against a constant external pressure of 20 bar, and
(iii) a two stage compression consisting initially of compression against a constant external pressure of 10 bar until Pgas=Pext, followed by compression against a constant pressure of 20 bar until Pgas=Pext
Work done on the gas in single stage compression is :
View SolutionIf the boundary of system moves by an infinitesimal amount, the work involved is given by dw=−PextdV
for irreversible process w=−PextΔV (where ΔV=Vf−Vi)
for reversible process Pext=Pint±dP≅Pint
so for reversible isothermal process w=−nRTln.VfVi
2mole of an ideal gas undergoes isothermal compression along three different plaths :
(i) reversible compression from Pi=2 bar and Vi=8L to Pf=20 bar
(ii) a single stage compression against a constant external pressure of 20 bar, and
(iii) a two stage compression consisting initially of compression against a constant external pressure of 10 bar until Pgas=Pext, followed by compression against a constant pressure of 20 bar until Pgas=Pext
Work done (in bar-L) on the gas in reversible isothermal compression is :
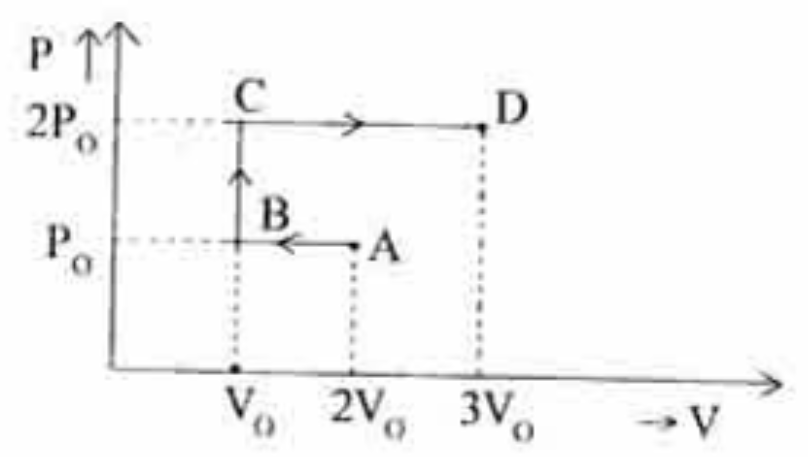
View SolutionThe work done by the gas in the process shown in given P-V diagram is
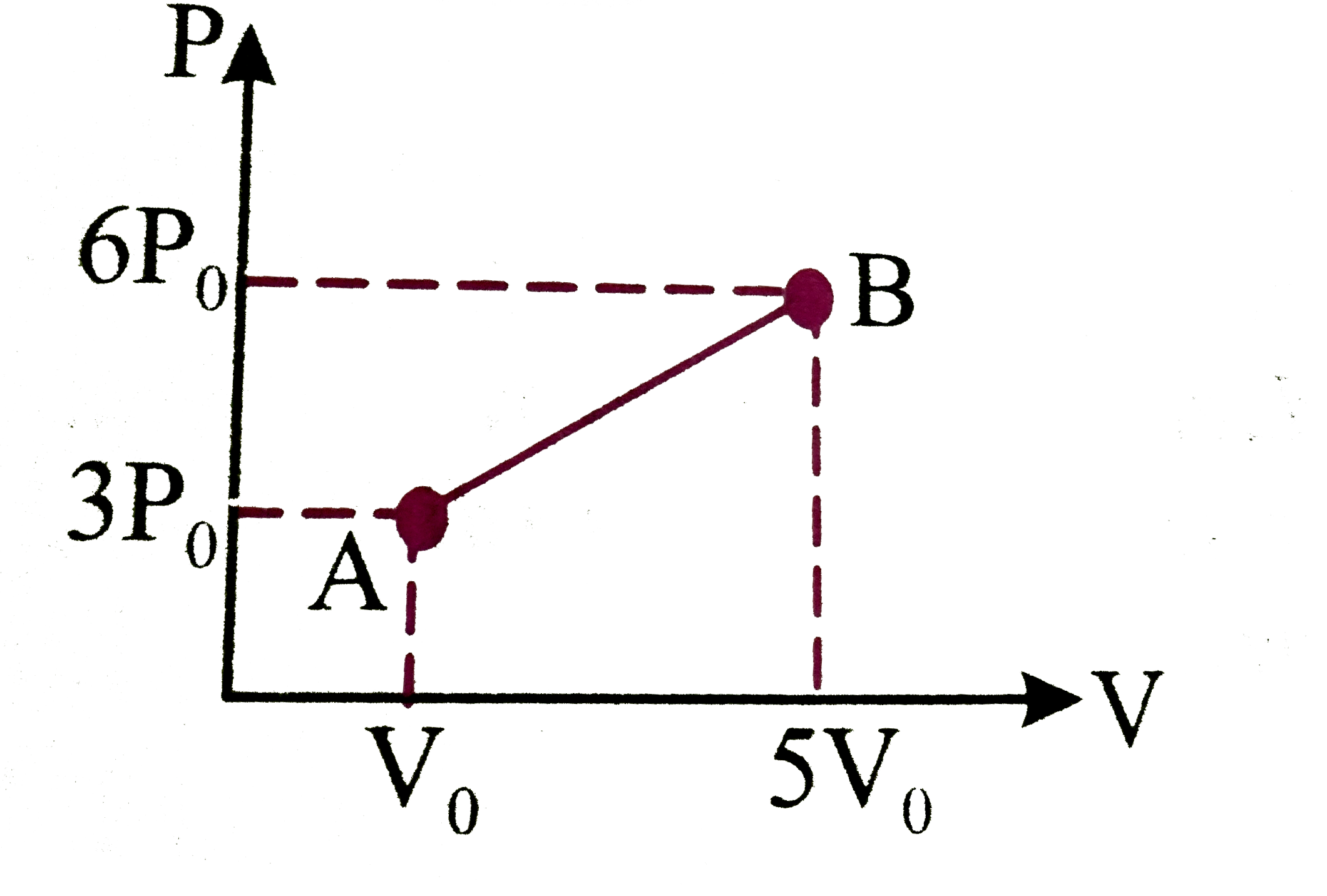
View SolutionOne mole of a monoatomic ideal gas undergoes the process A→B in the given P-V diagram. What is the specific heat for this process?
View SolutionA sample of gas is compressed from an initial volume of 2v0 to v0 using three different processes.
First: Using reversible isothermal
Second: Using reversible adiabatic
Third: Using irreversible adiabatic under a constant external pressure then
View SolutionFor a reversible process at T = 300K, the volume is increased from Vi=1L to Vf=10L. Calculate ΔH if the process is isothermal -
View SolutionA gas is expanded from volume V1 to V2 through three different process:
a. Reversible adiabatic
b. Reversible isothermal
c. Irreversible adiabatic (against a constant external pressure Pex)
The correct option is
View SolutionTwo moles of an ideal gas undergo the following process :
(a) a reversible isobaric expansion from (P atm, VL) to (P atm , 2VL).
(b) a reversible isochoric change of state from (P atm , 2V,L) to (P/2 atm, 2VL)
(c) a reversible isothermal compression from (P/2 atm, 2VL) to (P atm, VL).
Sketch with labels each of the processes on the same P−V diagram.
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
If P3 and P2 are equal, then
View Solution
