In a closed rigid container an ideal gas is filled. If the gas is heated, the graph of pressure (P) v/s root mean square speed (rms) will be :
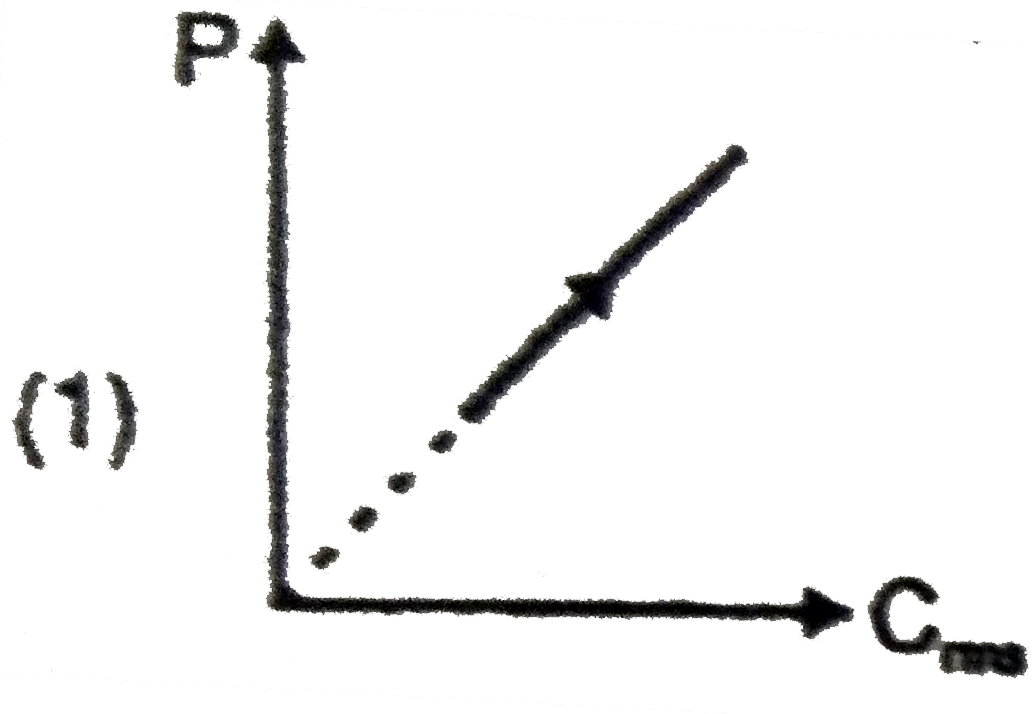
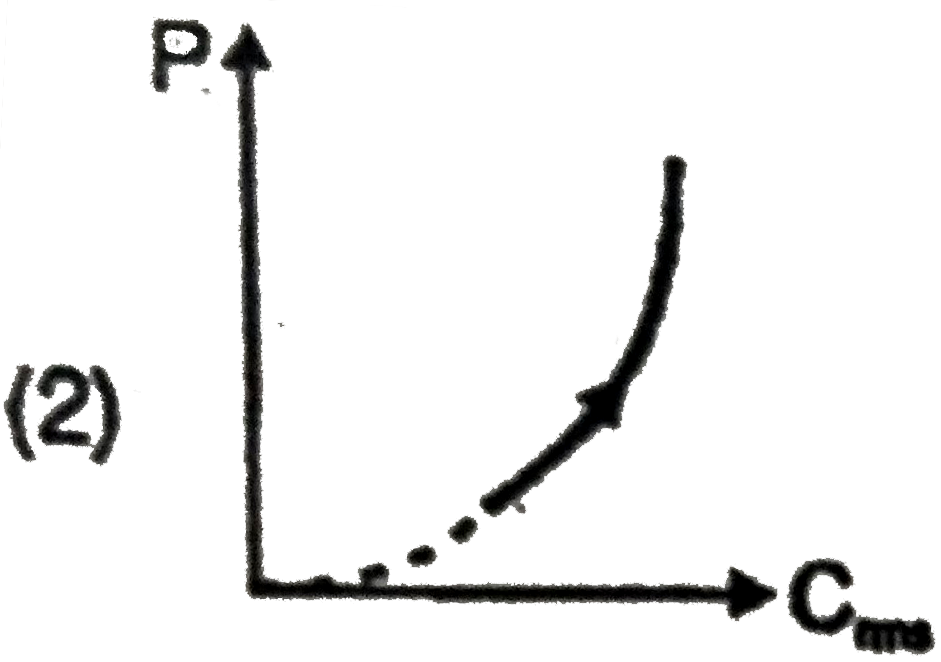
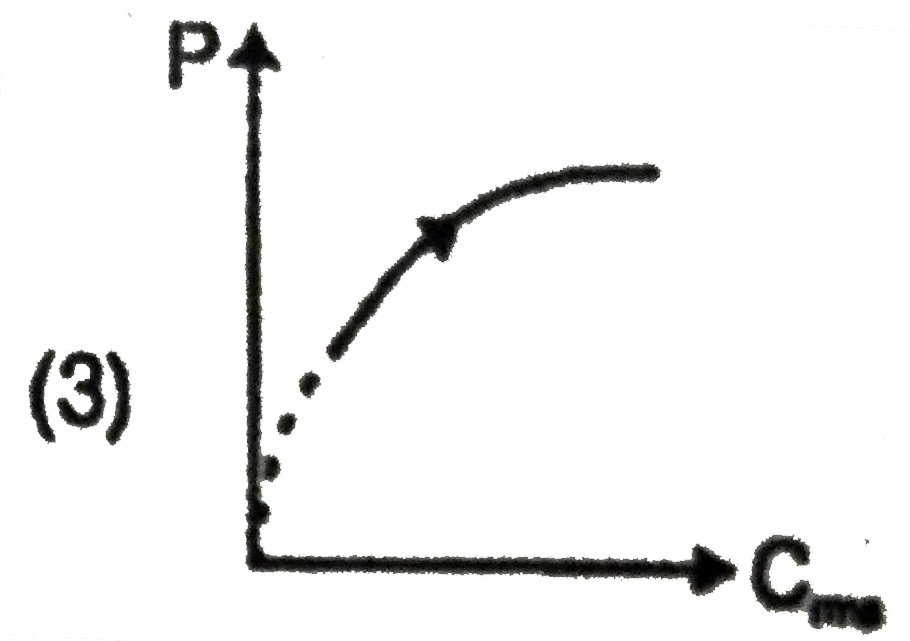

The correct Answer is:B
To solve the problem of determining the relationship between pressure (P) and root mean square speed (C_rms) of an ideal gas in a closed rigid container when heated, we can follow these steps:
1. Understand the Ideal Gas Law:
The ideal gas law is given by the equation:
PV=nRT
where P is pressure, V is volume, n is the number of moles, R is the ideal gas constant, and T is the absolute temperature.
2. Identify the Conditions:
In this problem, we have a closed rigid container. This means that the volume V is constant.
3. Relate Pressure to Temperature:
Since the volume is constant, we can rearrange the ideal gas law to express pressure in terms of temperature:
P=nRTV
This shows that pressure P is directly proportional to temperature T:
P∝T
4. Relate Root Mean Square Speed to Temperature:
The root mean square speed Crms of an ideal gas is given by the equation:
Crms=√3RTM
where M is the molar mass of the gas. From this equation, we can see that Crms is also directly proportional to the square root of temperature:
Crms∝√T
5. Square the Relationship of RMS Speed:
To relate pressure and Crms, we can square the relationship for Crms:
C2rms∝T
Thus, we can express temperature in terms of Crms:
T∝C2rms
6. Combine the Relationships:
Since we have established that P∝T and T∝C2rms, we can combine these relationships:
P∝C2rms
7. Conclusion on the Graph:
The relationship P∝C2rms indicates that pressure is proportional to the square of the root mean square speed. This means that if we plot pressure P against Crms, the graph will be a parabola opening upwards, not a straight line.
Final Answer:
The graph of pressure (P) versus root mean square speed (C_rms) will be a curve that shows that pressure increases with the square of the root mean square speed.
The ideal gas law is given by the equation:
PV=nRT
where P is pressure, V is volume, n is the number of moles, R is the ideal gas constant, and T is the absolute temperature.
In this problem, we have a closed rigid container. This means that the volume V is constant.
Since the volume is constant, we can rearrange the ideal gas law to express pressure in terms of temperature:
P=nRTV
This shows that pressure P is directly proportional to temperature T:
P∝T
The root mean square speed Crms of an ideal gas is given by the equation:
Crms=√3RTM
where M is the molar mass of the gas. From this equation, we can see that Crms is also directly proportional to the square root of temperature:
Crms∝√T
To relate pressure and Crms, we can square the relationship for Crms:
C2rms∝T
Thus, we can express temperature in terms of Crms:
T∝C2rms
Since we have established that P∝T and T∝C2rms, we can combine these relationships:
P∝C2rms
The relationship P∝C2rms indicates that pressure is proportional to the square of the root mean square speed. This means that if we plot pressure P against Crms, the graph will be a parabola opening upwards, not a straight line.
The graph of pressure (P) versus root mean square speed (C_rms) will be a curve that shows that pressure increases with the square of the root mean square speed.
Topper's Solved these Questions
Similar Questions
If an ideal gas is heated at constant pressure :
View SolutionA closed box contains an ideal gas if temperature of gas increased which
View SolutionWhat is the relation between average speed and root mean square speed for a gas ?
View Solutiongraph of an ideal gas is as shown in figure.
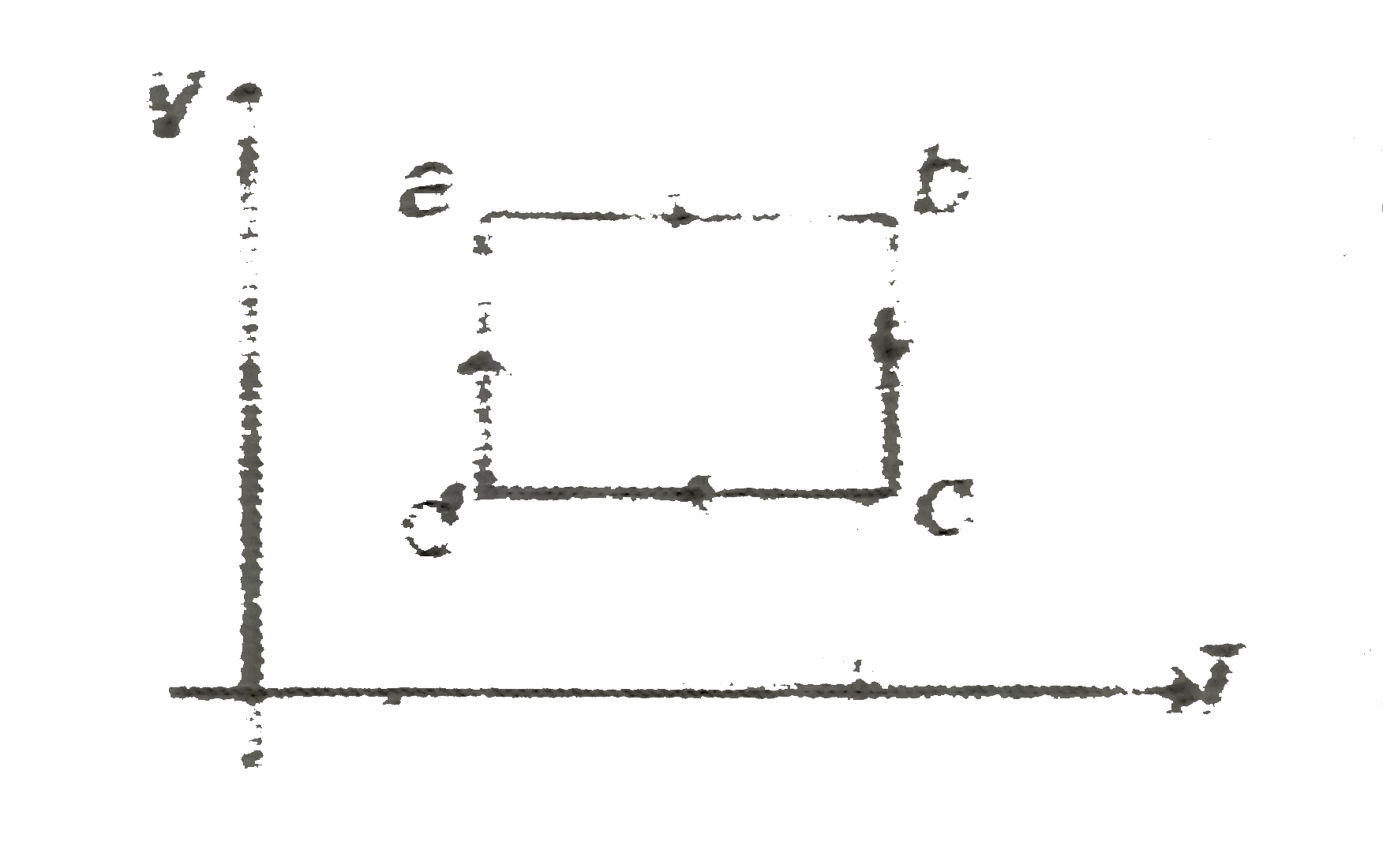
Heat is supplied to the gas in process (s).
View SolutionThe ratio of everage speed, most probable speed and root mean square speed of a gas sample will be
View SolutionA gas at the temperature 250 K is contained in a closed vessel. If the gas is heated through 1K, then the percentage increase in its pressure will be
View SolutionA gas at the temperature 250 K is contained in a closed vessel. If the gas is heated through 1K, then the percentage increase in its pressure will be
View SolutionRoot mean square speed of an ideal gas at 300 K is 500 m/s. Temperature is increased four times then root mean square speed will become
View SolutionThe energy density uV of an ideal gas is related to its pressure P as
View SolutionThe r.m.s speed of the molecules of an ideal gas Is V0 If pressure of the gas is halved but temperature is kept constant then r.m.s. speed of the gas molecule will be
View Solution