A vessel is partly filled with liquid. When the vessel is cooled to a lower temperature, the space in the vessel unoccupied by the liquid remains constant. Then the volume of the liquid (VL), volume of the vessel (VV) the coefficient of cubical expansion of the material of the vessel (γV) and of the liquid (γL) are related as :
γL>γv
γL<γv
γvγL=VC/VL
γvγL=VL/VC
The correct Answer is:A
ΔVL=ΔVV⇒γLVL=γvVv or γLγv=VvVL
But Vv>VL⇒γL>γv
Topper's Solved these Questions
Similar Questions
A vessel is partly filled with liquid. When the vessel is cooled to a lower temperature, the space in the vessel unoccupied by the liquid remains constant. Then the volume of the liquid (VL) volume of the vessel (VV) the coefficient of cubical expansion of the material of the vessel (γv) and of the solid (γL) are related as
View SolutionLet γ : coefficient of volume expansion of the liquid and α : coefficient of linear expansion of the material of the tube
View SolutionA vessel is partly filled with a liquid. Coefficients of cubical expansion of material of the vessel and liquid are γv unoccupied by the liquid will necessarily
View SolutionA vessel is partly filled with a liquid. Coefficients of cubical expansion of material of the vessel and liquid are γv and γL , then the volume unoccupied by the liquid will necessarily
View SolutionAir is filled at 60∘C in a vessel of open mouth. The vessel is heated to a temperature T so that 1/4th of air escapes. Assuming the volume of vessel remaining constant, the value of T is
View SolutionA glass vessel of volume 100cm3 is filled with mercury and is heated from 25∘C→75∘C. What volume of mercury will overflow? Coefficient of linear expansion of glass =1.8×10−6/'∘C and coefficient of volume expansion of mercury is 1.8×10−4/'∘C.
View SolutionThe absolute coefficient of expansion of a liquid is 7 times that the volume coefficient of expansion of the vessel. Then the ratio of absolute and apparent expansion of the liquid is
View SolutionThe absolute coefficient of expansion of a liquid is 7 times that the volume coefficient of expansion of the vessel. Then the ratio of absolute and apparent expansion of the liquid is
View SolutionThe apparent depth of a liquid in a vessel is 15 cm, when its real depth is 20 cm. find the refractive index of the liquid.
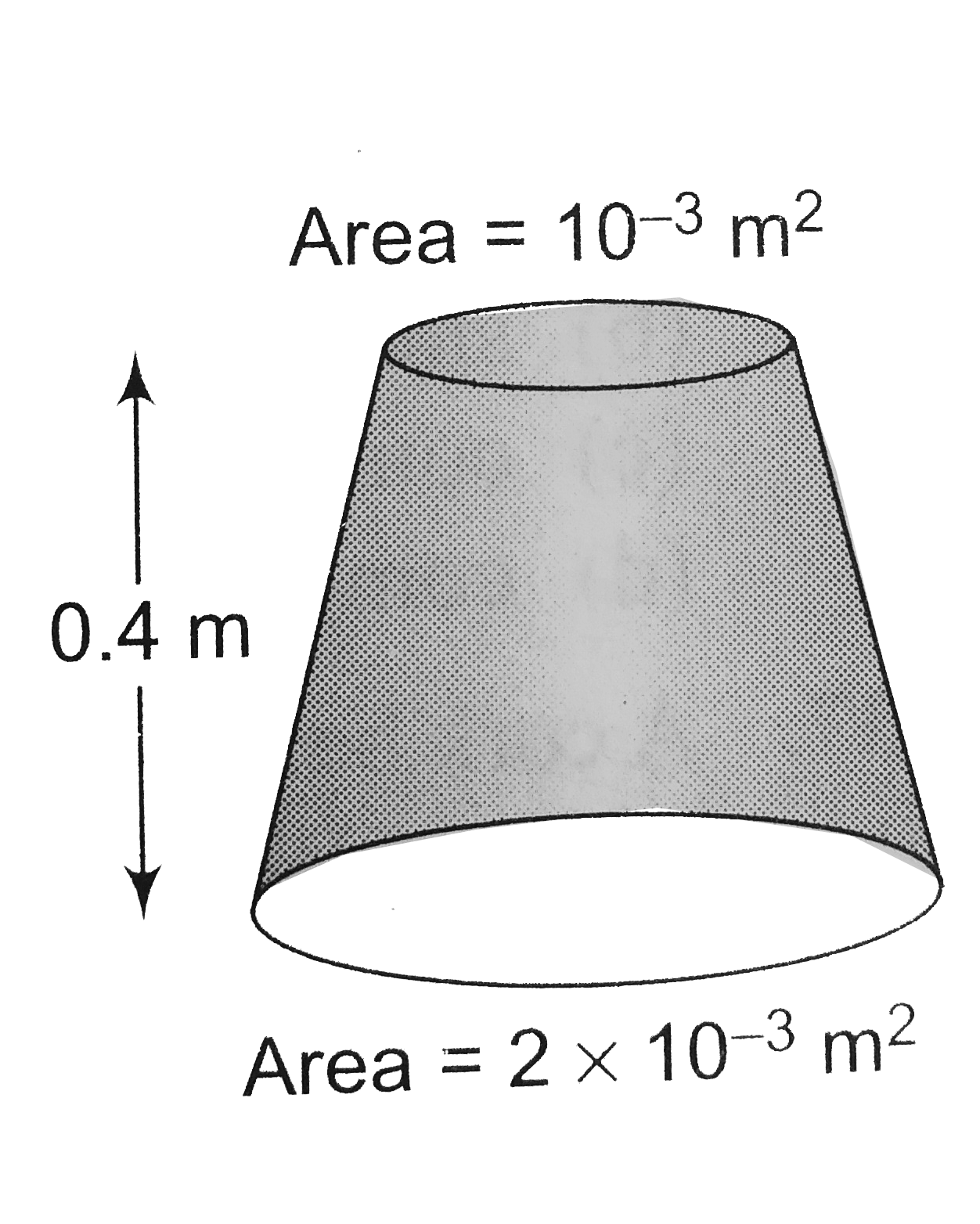
View SolutionA uniformly tapering vessel is filled with a liquid of density 900km/m3. The force that acts on the base of the vessel due to the liquid is (g=10ms−2)
View Solution