The apparent depth of a liquid in a vessel is 15 cm, when its real depth is 20 cm. find the refractive index of the liquid.
To find the refractive index of the liquid based on the given apparent and real depths, follow these steps:
1. Identify Given Values:
- Apparent Depth (d') = 15 cm
- Real Depth (d) = 20 cm
2. Use the Formula for Refractive Index:
The refractive index (n) of a medium can be calculated using the formula:
n=Real DepthApparent Depth
3. Substitute the Values into the Formula:
n=20 cm15 cm
4. Calculate the Refractive Index:
n=2015=43≈1.33
5. Conclude the Result:
The refractive index of the liquid is approximately 1.33.
Final Answer:
The refractive index of the liquid is 1.33.
---
- Apparent Depth (d') = 15 cm
- Real Depth (d) = 20 cm
The refractive index (n) of a medium can be calculated using the formula:
n=Real DepthApparent Depth
n=20 cm15 cm
n=2015=43≈1.33
The refractive index of the liquid is approximately 1.33.
The refractive index of the liquid is 1.33.
Topper's Solved these Questions
- REFRACTION OF LIGHT AT PLANE SURFACESBook:ICSEChapter:REFRACTION OF LIGHT AT PLANE SURFACESExercise:EXERCISE-4(A)
Explore 31 Videos
- REFRACTION OF LIGHT AT PLANE SURFACESBook:ICSEChapter:REFRACTION OF LIGHT AT PLANE SURFACESExercise:EXERCISE-4(A) MULTIPLE CHOICE TYPE
Explore 3 Videos
- REFRACTION OF LIGHTBook:ICSEChapter:REFRACTION OF LIGHTExercise:DIAGRAM BASED MCQ:
Explore 5 Videos
- REFRACTION THROUGH A LENS Book:ICSEChapter:REFRACTION THROUGH A LENS Exercise:EXERCISE-5(D) (MULTIPLE CHOICE TYPE)
Explore 2 Videos
Similar Questions
A mark at the bottom of a liquid appears to rise by 0.1m. The depth of the liquid is 1m. The refractive index of the liquid is
View SolutionIn a vessel, as shown in Figure., point P is just visible when no liquid is filled in vessel through a telescope in the air. When liquid is filled in the vessel completely, point Q is visible without movint the vessel or telescope. Find the refractive index of the liquid.
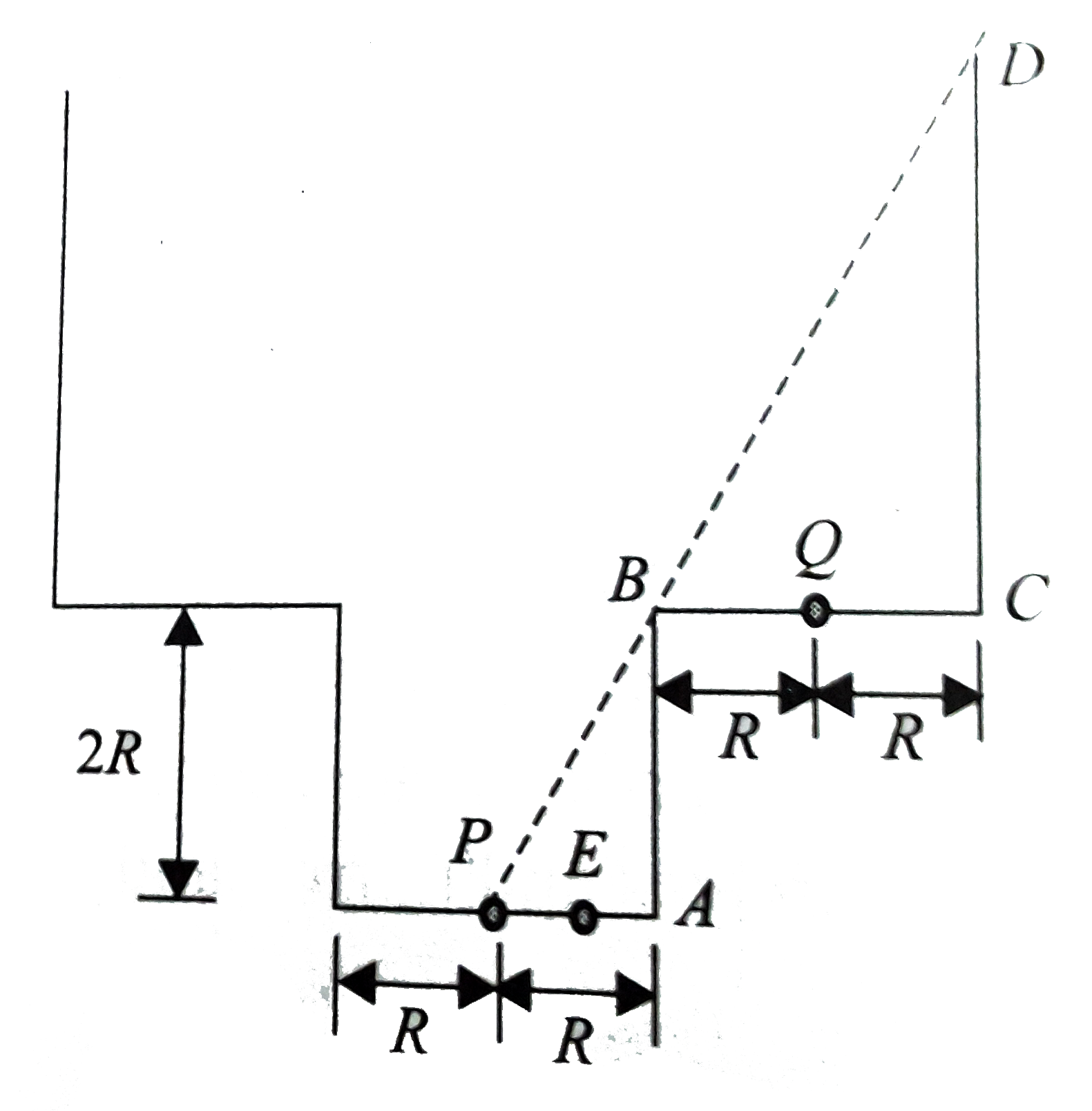
View Solution
Knowledge Check
The apparent depth of a needle laying at the bottom of the tank, which is filled with water of refractive index 1.33 to a height of 12.5 cm is measured by a microscope to be 9.4cm. If water is replaced by a liquid of refractive index 1.63 upto the same height. What distance would the microscope have to be moved to focus on the needle again ?
A1.73cmB2.13cmC1.5cmD2.9cm
A layer of oil 3 cm thick is floating on a layer of coloured water 5 cm thick. Refractive index of coloured water is 5/3 and the apparent depth of the two liquids appears to be 36/7cm. Find the refractive index of oil.
View SolutionFig. shows an equiconvex lens (of refractive index 1.5) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be 45.0cm. The liquid is removed and the experiment is repeated. The new distance is measured to be 30.0cm. What is the refractive index of the liquid ?
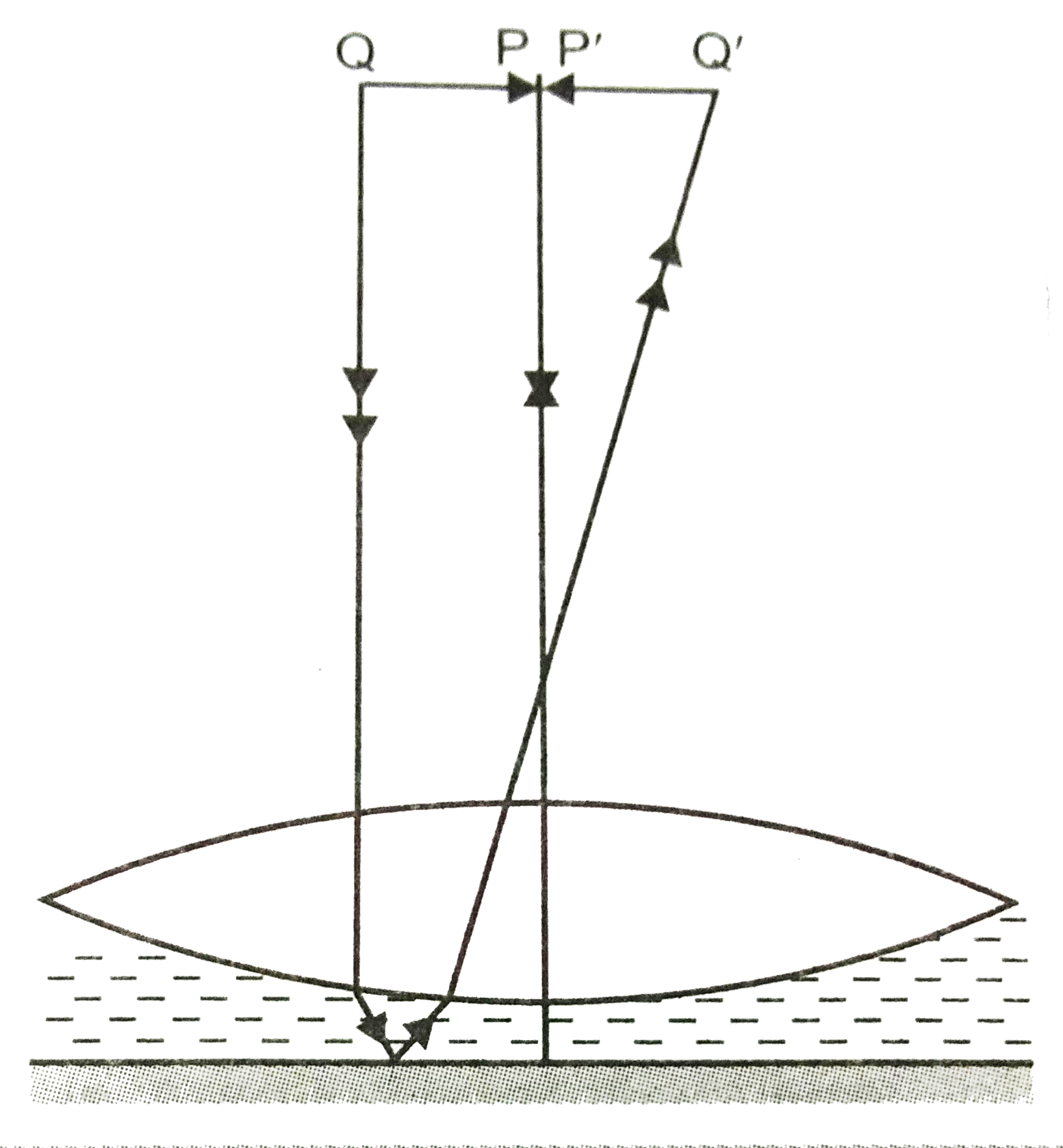
View SolutionA convex lens is held 45cm above the bottom of an empty tank. The image of a point at the bottom of a tank is formed 36cm above the lens. Now, a liquid is poured into the tank to a depth of 40cm. It is found that the distance of the image of the same point on the bottom of the tank is 48cm above the lens. Find the refractive index of the liquid.
View SolutionA transparent cube of 15cm edge contains a small air bubble. Its apparent depth when viewed through one face is 6cm and when viewed through the opposite face is 4cm. Then the refractive index of the material of the cube is
View SolutionA transparent cube of 15cm edge contains a small air bubble. Its apparent depth when viewed through one face is 6cm and when viewed through the opposite face is 4cm. Then the refractive index of the material of the cube is
View SolutionA transparent cube contains a small air bubble. Its apparent distance is 2 cm when seen through other facel. If the refractive index of the material of the cube is 1.5, the real length of the edge of cube must be
View SolutionWhen entire Young's double slit apparatus is immersed in a liquid the fringe width decreases by 20∘. The refractive index of the liquid is
View Solution

