A photographic film is coated with a silver bromide layer. When light falls on this film, silver bromide molecules dissociate and the film records the light there. A minimum of 0.6 e V is needed to dissociate a silver bromide molecule. Find the maximum wavelength of light that can be recorded by the film.
To find the maximum wavelength of light that can be recorded by a photographic film coated with a silver bromide layer, we need to use the relationship between energy and wavelength. Here’s a step-by-step solution:
Step 1: Understand the Energy-Wavelength Relationship
The energy (E) of a photon can be expressed in terms of its wavelength (λ) using the formula:
E=hcλ
where:
- E is the energy in joules,
- h is Planck's constant (6.63×10−34Js),
- c is the speed of light (3×108m/s),
- λ is the wavelength in meters.
Step 2: Relate Energy to Wavelength
Given that a minimum energy of 0.6 eV is required to dissociate a silver bromide molecule, we need to convert this energy into joules. The conversion factor is:
1eV=1.6×10−19J
Thus,
E=0.6eV=0.6×1.6×10−19J=9.6×10−20J
Step 3: Rearrange the Formula to Find Wavelength
From the energy-wavelength relationship, we can rearrange the formula to find the wavelength:
λ=hcE
Step 4: Substitute the Values
Now we can substitute the values of h, c, and E into the equation:
λ=(6.63×10−34Js)×(3×108m/s)9.6×10−20J
Step 5: Calculate the Wavelength
Calculating the above expression:
λ=1.989×10−259.6×10−20≈2.07×10−7m
Converting this to nanometers:
λ≈2071nm
Final Answer
The maximum wavelength of light that can be recorded by the film is approximately 2071 nm.
---
The energy (E) of a photon can be expressed in terms of its wavelength (λ) using the formula:
E=hcλ
where:
- E is the energy in joules,
- h is Planck's constant (6.63×10−34Js),
- c is the speed of light (3×108m/s),
- λ is the wavelength in meters.
Given that a minimum energy of 0.6 eV is required to dissociate a silver bromide molecule, we need to convert this energy into joules. The conversion factor is:
1eV=1.6×10−19J
Thus,
E=0.6eV=0.6×1.6×10−19J=9.6×10−20J
From the energy-wavelength relationship, we can rearrange the formula to find the wavelength:
λ=hcE
Now we can substitute the values of h, c, and E into the equation:
λ=(6.63×10−34Js)×(3×108m/s)9.6×10−20J
Calculating the above expression:
λ=1.989×10−259.6×10−20≈2.07×10−7m
Converting this to nanometers:
λ≈2071nm
The maximum wavelength of light that can be recorded by the film is approximately 2071 nm.
Topper's Solved these Questions
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBook:HC VERMA ENGLISHChapter:PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYExercise:question for short answer
Explore 13 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBook:HC VERMA ENGLISHChapter:PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYExercise:objective II
Explore 7 Videos
- PERMANENT MAGNETSBook:HC VERMA ENGLISHChapter:PERMANENT MAGNETSExercise:Short Answer
Explore 11 Videos
- PHOTOMETRYBook:HC VERMA ENGLISHChapter:PHOTOMETRYExercise:All Questions
Explore 38 Videos
Similar Questions
A light of wavelength 5890Å falls normally on a thin air film. The minimum thickness of the film such that the film appears dark in reflected light is
View SolutionIn a doulble slit experiment when a thin film of thickness t having refractive index μ is introduced in from of one of the slits, the maximum at the centre of the fringe pattern shifts by one width. The value of t is (λ is the wavelength of the light used)
View SolutionThe light sensitive compound on most photographic films is silver bromide AgBr. A film is exposed when the light energy of dissociation of AgBr is 105Jmol−1. For a photon that is just able to dissociate a molecule of AgBr, the photon energy is
View SolutionFind the minimum thickness of a film which will strongly reflect the light of wavelength 589 nm. The refractive index of the material of the film is 1.25.
View SolutionA film with index of refraction 1.50 coats a glass lens with index of refraction 1.80. What is the minimum thickness of the thin film that will strongly reflect light with wavelength 600 nm?
View SolutionYDSE is carried out in a liquid of refractive index μ=1.3 and a thin film of air is formed in front of the lower slit as shown in the figure. If a maxima of third order is formed at the origin O, find the thickness of the air film. Find the positions of the fourth maxima. The wavelength of light is air is λ0=0.78μm and D/d=1000.
View SolutionA thin oil film of refractive index 1.2 floats on the surface of water (μ=43). When a light of wavelength λ=9.6×10−7m falls normally on the film from air, then it appears dark when seen normally. The minimum change in its thickness for which it will appear bright in normally reflected light by the same light is:
View Solution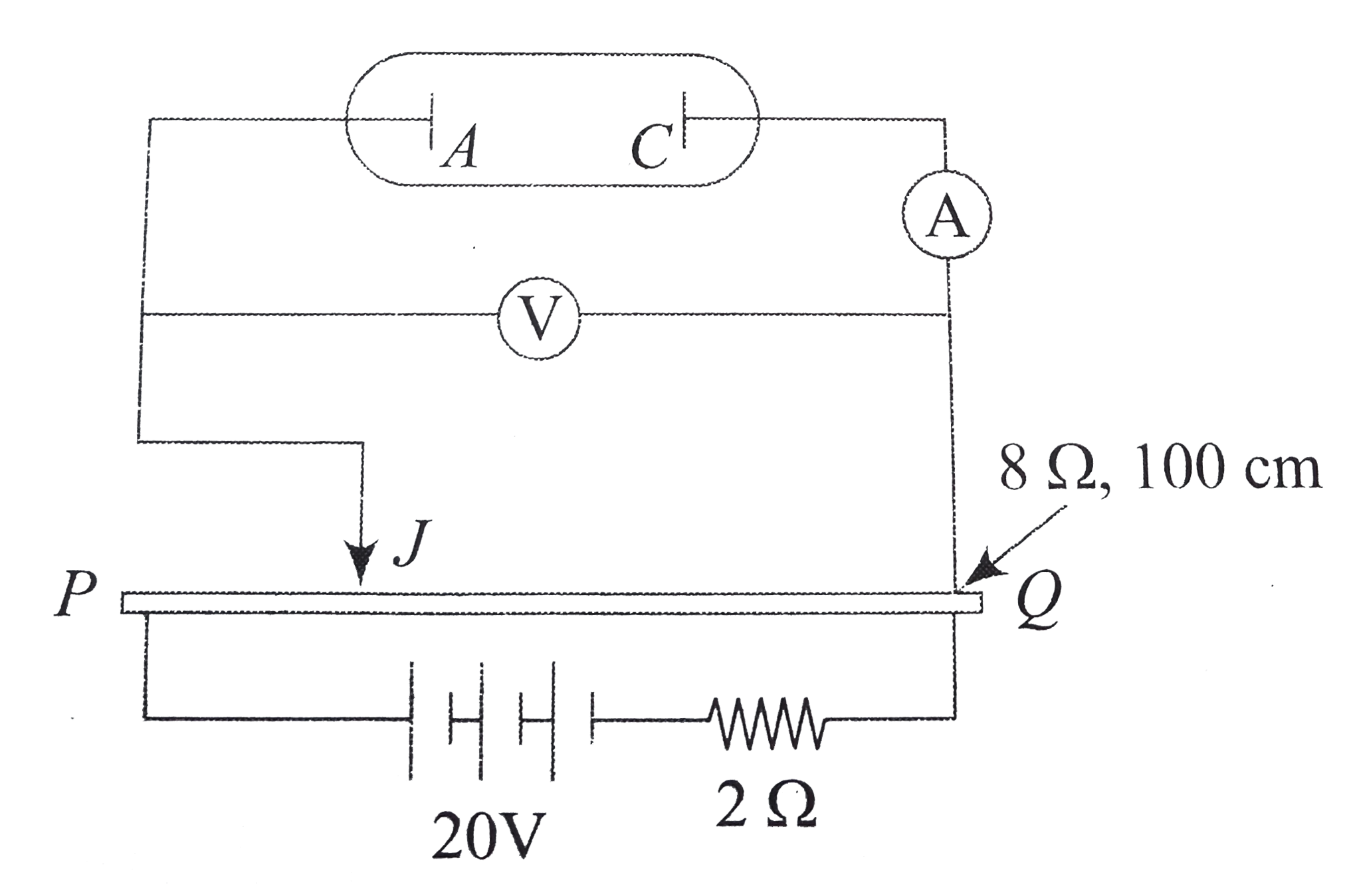
An experimental setup of verification of photoelectric effect is shown if Fig. The voltage across the electrodes is measured with the help of an ideal voltmeter, and which can be varied by moving jockey J on the potentiometer with wire. The battery used in potentiometer circuit is of 20 V and its internal resistance is 2Ω. The resistance of 100 cm long potentiometer wire is 8Ω.
The photocurrent is measured with the help of an ideal ammeter. Two plates of potassium oxide of area 50cm2 at separation 0.5mm are used in the vacuum tube. Photocurrent in the circuit is very small, so we can treat the potentiometer circuit as an independent circuit. The wavelength of various colors is as follows:
Q. When other light falls on the anode plate, the ammeter reading remains zero till jockey is moved from the end P to the middle point of the wire PQ. Thereafter, the deflection is recorded in the ammeter. The maximum kinetic energy of the emitted electron is
View SolutionRefractive index of a thin soap film of a uniform thickness is 1.34. Find the smallest thickness of the film that gives in interference maximum in the reflected light when light of wavelength 5360Å fall at normal incidence.
View SolutionA parallel beam of light of wavelength 560 nm falls on a thin film of oil (refractive index = 1.4). What should be the minimum thickness of the film so that it strongly transmit the light ?
View Solution