In an experiment on photoelectric effect, the stopping potential is measured for monochromatic light beams corresponding to different wavelength. The data collected are as follows:
wavelength (nm): 350 400 450 500 550
stopping potential (V): 1.45 1.00 0.66 0.38 0.16
Plot the stopping potential against inverse of wavelength on a graph paper and find (a) the Planck constant, (b) the work function of the emitter and (c) the threshold wavelength .
To solve the problem step by step, we will follow the instructions provided in the video transcript and derive the required values.
Step 1: Data Preparation
We have the following data for wavelength (in nm) and stopping potential (in volts):
| Wavelength (nm) | Stopping Potential (V) |
|------------------|------------------------|
| 350 | 1.45 |
| 400 | 1.00 |
| 450 | 0.66 |
| 500 | 0.38 |
| 550 | 0.16 |
Step 2: Calculate the Inverse of Wavelength
Convert the wavelengths from nanometers to meters and calculate the inverse of the wavelength (1/λ):
- For λ = 350 nm: 1λ=1350×10−9
- For λ = 400 nm: 1λ=1400×10−9
- For λ = 450 nm: 1λ=1450×10−9
- For λ = 500 nm: 1λ=1500×10−9
- For λ = 550 nm: 1λ=1550×10−9
Step 3: Plotting the Graph
Plot the stopping potential (V) on the y-axis and the inverse of the wavelength (1/λ) on the x-axis.
Step 4: Determine the Equation of the Line
From the photoelectric effect equation:
eV0=hcλ−ϕ
Rearranging gives:
V0=hce⋅1λ−ϕe
This resembles the linear equation y=mx+c, where:
- y=V0
- x=1λ
- Slope m=hce
- Intercept c=−ϕe
Step 5: Calculate the Planck Constant (h)
Using two data points, we can set up two equations:
1. For λ=350 nm:
1.45=hc350×10−9−ϕ
2. For λ=400 nm:
1.00=hc400×10−9−ϕ
Subtract the two equations to eliminate ϕ:
1.45−1.00=hc350×10−9−hc400×10−9
This simplifies to:
0.45=hc(1350×10−9−1400×10−9)
Calculating the right-hand side:
1350−1400=400−350350×400=50140000=12800
Thus:
0.45=hc⋅12800×10−9
Solving for h:
h=0.45⋅2800×10−9
Calculating gives:
h≈1.26×10−15 eV s
Step 6: Calculate the Work Function (φ)
Using the first equation:
1.45=hc350×10−9−ϕ
Substituting h and rearranging gives:
ϕ=hc350×10−9−1.45
Step 7: Calculate the Threshold Wavelength
Using the work function:
ϕ=hcλthreshold
Rearranging gives:
λthreshold=hcϕ
Final Answers
(a) Planck's constant h≈4.2×10−15 eV s
(b) Work function ϕ≈2.15 eV
(c) Threshold wavelength λthreshold≈576.8 nm
We have the following data for wavelength (in nm) and stopping potential (in volts):
|------------------|------------------------|
| 350 | 1.45 |
| 400 | 1.00 |
| 450 | 0.66 |
| 500 | 0.38 |
| 550 | 0.16 |
Convert the wavelengths from nanometers to meters and calculate the inverse of the wavelength (1/λ):
- For λ = 400 nm: 1λ=1400×10−9
- For λ = 450 nm: 1λ=1450×10−9
- For λ = 500 nm: 1λ=1500×10−9
- For λ = 550 nm: 1λ=1550×10−9
Plot the stopping potential (V) on the y-axis and the inverse of the wavelength (1/λ) on the x-axis.
From the photoelectric effect equation:
eV0=hcλ−ϕ
Rearranging gives:
V0=hce⋅1λ−ϕe
- y=V0
- x=1λ
- Slope m=hce
- Intercept c=−ϕe
Using two data points, we can set up two equations:
1. For λ=350 nm:
1.45=hc350×10−9−ϕ
2. For λ=400 nm:
1.00=hc400×10−9−ϕ
1.45−1.00=hc350×10−9−hc400×10−9
0.45=hc(1350×10−9−1400×10−9)
1350−1400=400−350350×400=50140000=12800
0.45=hc⋅12800×10−9
h=0.45⋅2800×10−9
h≈1.26×10−15 eV s
Using the first equation:
1.45=hc350×10−9−ϕ
ϕ=hc350×10−9−1.45
Using the work function:
ϕ=hcλthreshold
λthreshold=hcϕ
(a) Planck's constant h≈4.2×10−15 eV s
Topper's Solved these Questions
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - question for short answer
13 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - objective II
7 Videos
- PERMANENT MAGNETSBOOK - HC VERMA ENGLISHCHAPTER - PERMANENT MAGNETSEXERCISE - Short Answer
11 Videos
- PHOTOMETRYBOOK - HC VERMA ENGLISHCHAPTER - PHOTOMETRYEXERCISE - All Questions
38 Videos
Similar Questions
Knowledge Check
In photoelectric effect, stopping potential depends on
Afrequency of incident lightBnature of the emitter materialCintensity of incident lightDboth (a) and (b)
If stopping potentials corresponding to wavelengths 4000A and 4500A are 1.3 V and 0.9 V, respectively, then the work function of the metal is
View SolutionIn photoelectric effect the slope of stop of stopping potential versus frequency of incident light for a given surface will be
View SolutionDefine the term 'stopping potential' in relation to photoelectric effect.
View SolutionGraph between stopping potential and frequency of light as shown find the work function
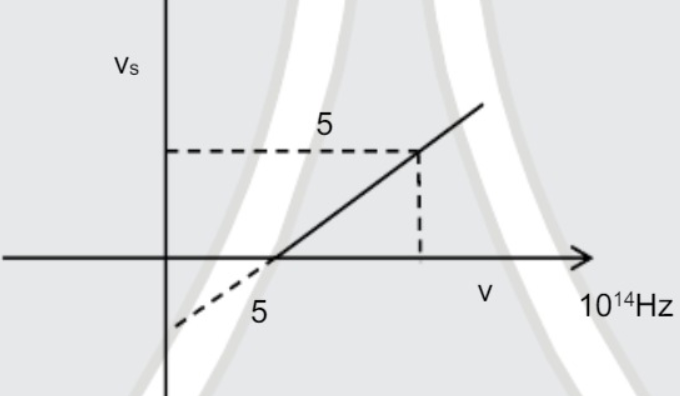
View SolutionIf the frequency of light in a photoelectric experiment is doubled the stopping potential will
View SolutionIn a photoelectric effect measurement, the stopping potential for a given metal is found to be V0 volt, when radiation of wavelength λ0 is used. If radiation of wavelength 2λ0 is used with the same metal, then the stopping potential (in V) will be
View SolutionFigure is the plot of the stopping potential versus the frequency of the light used in an experiment on photoelectric effect. Find (a) the ratio h/e and (b) the work function.
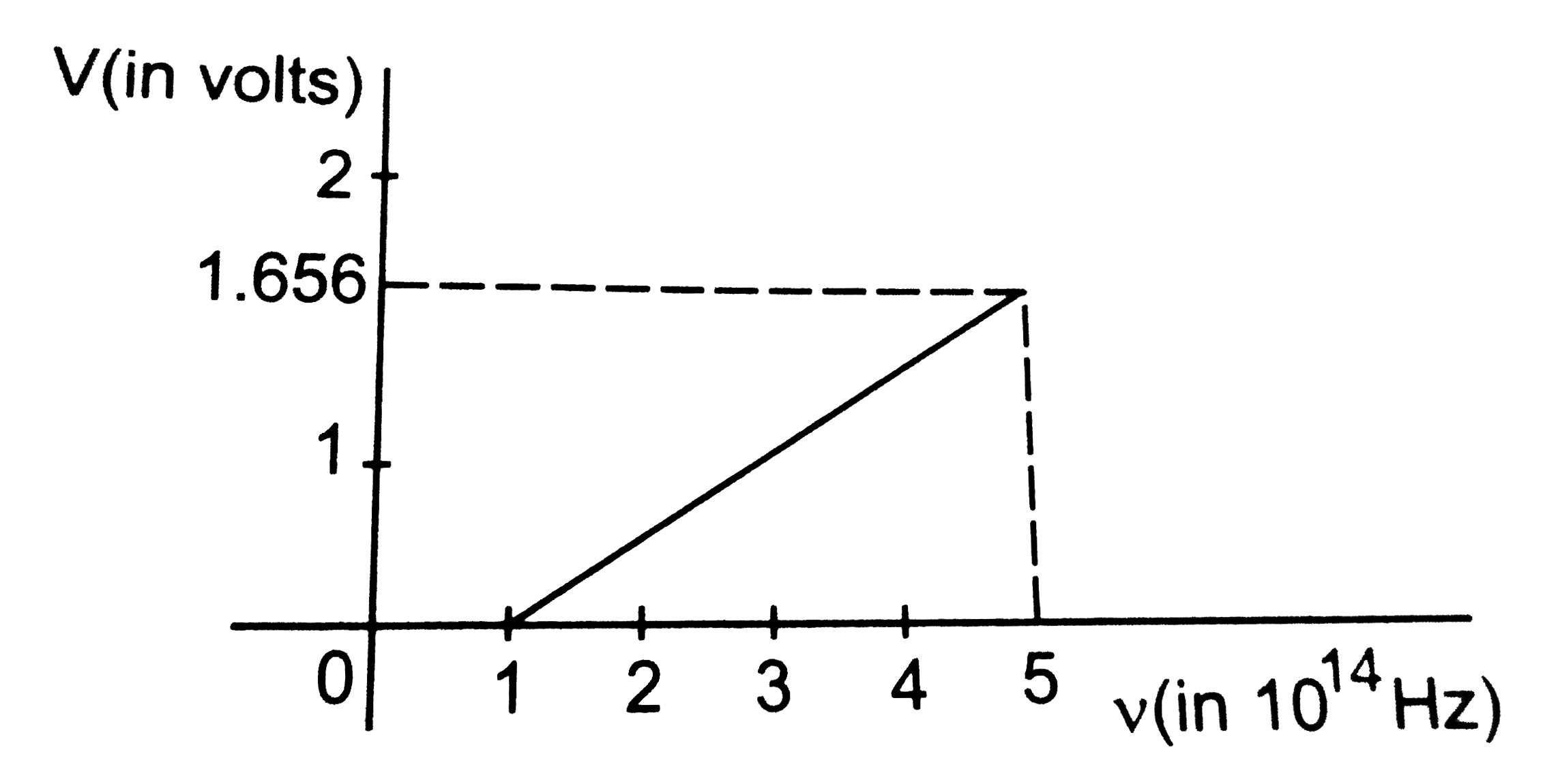
View Solution
