Consider the situation of the previous problem. Consider the fastest electron emitted parallel to the large metal plate. Find the displacement of this electron parallel to its initial velocity before it strikes the large metal plate.
To solve the problem of finding the displacement of the fastest electron emitted parallel to the large metal plate before it strikes the plate, we can follow these steps:
Step 1: Calculate the Electric Field
The electric field E can be calculated using the formula:
E=σϵ0
where:
- σ=1×10−9C/m2 (charge density)
- ϵ0=8.85×10−12C2/N m2 (permittivity of free space)
Substituting the values:
E=1×10−98.85×10−12≈113V/m
Step 2: Calculate the Acceleration of the Electron
The force F acting on the electron due to the electric field is given by:
F=qE
where:
- q=1.6×10−19C (charge of the electron)
Thus, the force becomes:
F=(1.6×10−19)×(113)≈1.81×10−17N
Now, using Newton's second law F=ma, we can find the acceleration a:
a=Fm
where m=9.1×10−31kg (mass of the electron):
a=1.81×10−179.1×10−31≈19.87×1012m/s2
Step 3: Calculate the Time of Flight
The time t taken for the electron to travel the vertical distance s=20cm=0.2m can be calculated using the equation:
s=ut+12at2
Assuming the initial vertical velocity u=0, we can simplify this to:
0.2=12(19.87×1012)t2
Solving for t2:
t2=0.2×219.87×1012≈2.01×10−14
Taking the square root:
t≈1.41×10−7s
Step 4: Calculate the Velocity of the Electron
Using the Einstein's photoelectric equation, we can find the kinetic energy of the emitted electron. Assuming the work function is ϕ=5eV and the energy of the photon is given by:
E=hcλ
where:
- h=6.626×10−34Js (Planck's constant)
- c=3×108m/s
- λ=400×10−9m
Calculating the energy of the photon:
E=(6.626×10−34)(3×108)400×10−9≈4.97×10−19J≈3.10eV
Thus, the kinetic energy KE of the electron is:
KE=E−ϕ=3.10−5=−1.90eV
However, since this value is negative, we need to ensure that the energy is sufficient for the electron to be emitted.
Step 5: Calculate the Horizontal Displacement
Using the velocity v calculated from the kinetic energy:
KE=12mv2⇒v2=2×KEm
Substituting the values:
v=√2×(1.2×1.6×10−19)9.1×10−31≈0.665×106m/s
Finally, calculate the horizontal displacement s:
s=vt=(0.665×106)×(1.41×10−7)≈0.092m=9.2cm
Final Answer
The displacement of the electron parallel to its initial velocity before it strikes the large metal plate is approximately 9.2 cm.
---
The electric field E can be calculated using the formula:
E=σϵ0
where:
- σ=1×10−9C/m2 (charge density)
- ϵ0=8.85×10−12C2/N m2 (permittivity of free space)
E=1×10−98.85×10−12≈113V/m
The force F acting on the electron due to the electric field is given by:
F=qE
where:
- q=1.6×10−19C (charge of the electron)
F=(1.6×10−19)×(113)≈1.81×10−17N
a=Fm
where m=9.1×10−31kg (mass of the electron):
a=1.81×10−179.1×10−31≈19.87×1012m/s2
The time t taken for the electron to travel the vertical distance s=20cm=0.2m can be calculated using the equation:
s=ut+12at2
Assuming the initial vertical velocity u=0, we can simplify this to:
0.2=12(19.87×1012)t2
Solving for t2:
t2=0.2×219.87×1012≈2.01×10−14
Taking the square root:
t≈1.41×10−7s
Using the Einstein's photoelectric equation, we can find the kinetic energy of the emitted electron. Assuming the work function is ϕ=5eV and the energy of the photon is given by:
E=hcλ
where:
- h=6.626×10−34Js (Planck's constant)
- c=3×108m/s
- λ=400×10−9m
E=(6.626×10−34)(3×108)400×10−9≈4.97×10−19J≈3.10eV
Thus, the kinetic energy KE of the electron is:
KE=E−ϕ=3.10−5=−1.90eV
However, since this value is negative, we need to ensure that the energy is sufficient for the electron to be emitted.
Using the velocity v calculated from the kinetic energy:
KE=12mv2⇒v2=2×KEm
Substituting the values:
v=√2×(1.2×1.6×10−19)9.1×10−31≈0.665×106m/s
s=vt=(0.665×106)×(1.41×10−7)≈0.092m=9.2cm
The displacement of the electron parallel to its initial velocity before it strikes the large metal plate is approximately 9.2 cm.
Topper's Solved these Questions
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - question for short answer
13 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - objective II
7 Videos
- PERMANENT MAGNETSBOOK - HC VERMA ENGLISHCHAPTER - PERMANENT MAGNETSEXERCISE - Short Answer
11 Videos
- PHOTOMETRYBOOK - HC VERMA ENGLISHCHAPTER - PHOTOMETRYEXERCISE - All Questions
38 Videos
Similar Questions
Consider the situation of the previous question from a frame moving with a speed v0 parallel to the initial velocity of the block? b. What is the work done by the kinetic friction?
View SolutionConsider the situation described in the previous example. A particle of mass m having a charge q is placed at a distance d from the metal sheet and is projected towards it. Find the maximum velocity of projection for which the particle does not hit the sheet.
View Solution
Knowledge Check
A parallel- plate capacitor with plate area A and separation between the plates d, is charged by a constant current i. Consider a plane surface of area A/2 parallel to the plates and drawn symmetrically between the plates. Find the displacement current through this area.
AIBI2CI4DI8
The' distance between the plates of a parallel plate capacitor is d. A metal plate of thickness d/2 is placed between the plates. What will e its effect on the capacitance.
View SolutionConsider the arrangement of parallel plates of the previous problem. If 1.0 nC charge is given to the upper plate instead of the middle, what will be the potential difference (in V) between (a) the upper and the middle plates and (b) the middle and the lower plates ? If Capacitance of each plate is 50 nF .
View SolutionConsider a parallel plate capacitor is charged by a constant current I, with plate area A and separation between the plates d. Consider a plane surface of area A/4 parallel to the plates and drawn symmetrically between the plates. Find the displacement current through this area.
View SolutionFrom what distance should a 100 eV electron be fired towards a large metal plate having a surface charge of −2.0×10−6Cm−2, so that it just fails to strike the plate ?
View SolutionA parallel- plate capacitor with plate area A and separation between the plates d, is charged by a constant current i. Consider a plane surface of area A/2 parallel to the plates and drawn summetrically between the plates. Find the displacement current through this area.
View SolutionA parallel- plate capacitor with plate area A and separation between the plates d, is charged by a constant current i. Consider a plane surface of area A/2 parallel to the plates and drawn summetrically between the plates. Find the displacement current through this area.
View Solution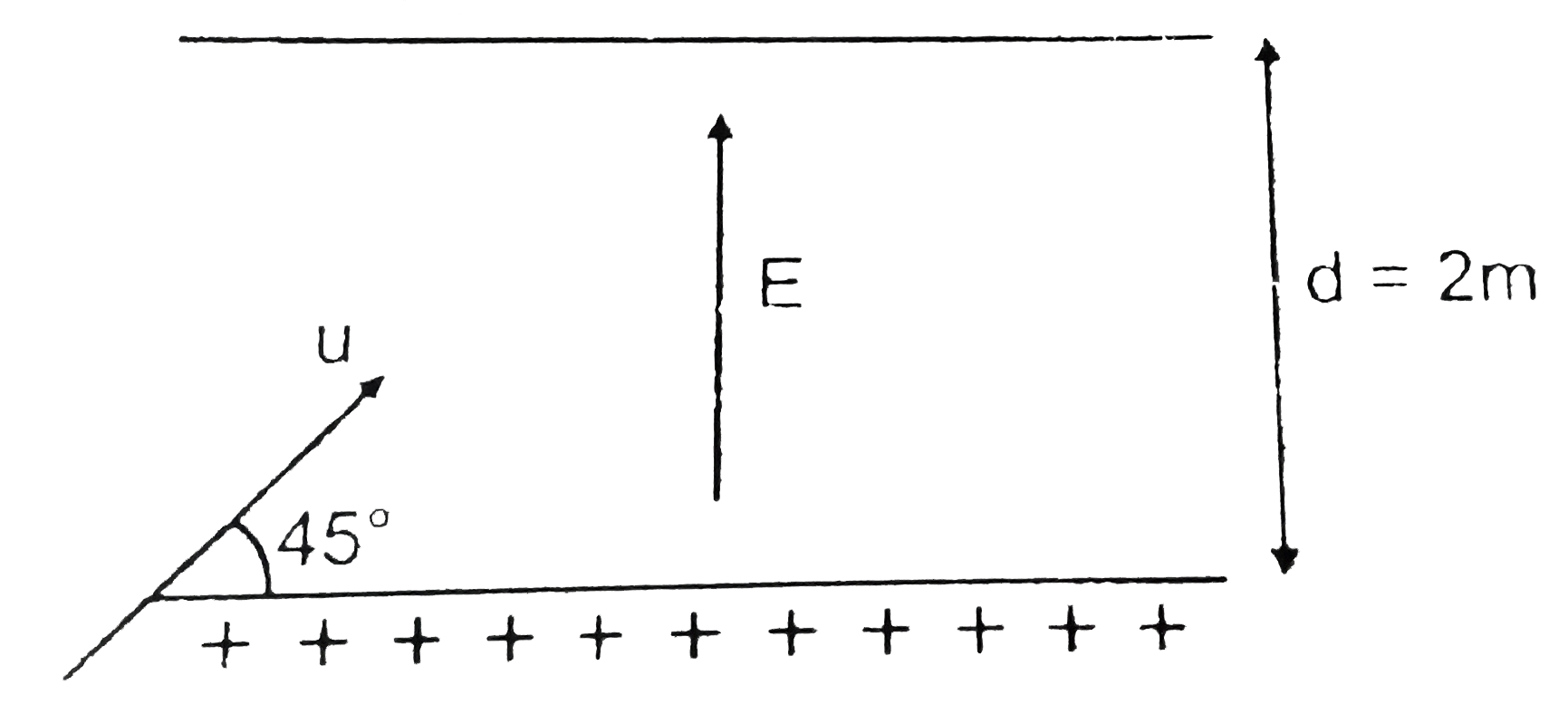
An electron is projected as shown with speed u. If electron just fails to strike the upper plate, find range. (distance from starting point at which electron strike the lower plate again). Consider only electric force.
View Solution
