A semicircular rods is joined at its end to a straight rod of the same material and the same cross-sectional area. The straight rod forms a diameter of the other rod. The junctions are maintained at different temperatures. Find the ratio of the heat transferred through a cross section of the straight rod in a given time.
The correct Answer is:B
To solve the problem of finding the ratio of heat transferred through a cross-section of the straight rod in a given time, we can follow these steps:
1. Understand the Setup: We have a semicircular rod (Rod 1) joined to a straight rod (Rod 2). Both rods are made of the same material and have the same cross-sectional area. The semicircular rod has a length equal to the arc length of a semicircle, while the straight rod has a length equal to the diameter of the semicircle.
2. Identify the Lengths:
- For the semicircular rod (Rod 1), if the radius is r, the length L1 is given by the formula for the arc length of a semicircle:
L1=πr
- For the straight rod (Rod 2), the length L2 is simply the diameter of the semicircle:
L2=2r
3. Write the Heat Transfer Formula: The rate of heat transfer Qt through a rod is given by Fourier's law of heat conduction:
Qt=kAΔTL
where:
- k is the thermal conductivity,
- A is the cross-sectional area,
- ΔT is the temperature difference,
- L is the length of the rod.
4. Calculate Heat Transfer for Each Rod:
- For the semicircular rod (Rod 1):
Q1t=kAΔTL1=kAΔTπr
- For the straight rod (Rod 2):
Q2t=kAΔTL2=kAΔT2r
5. Find the Ratio of Heat Transfer:
- To find the ratio of heat transfer through the two rods, we take the ratio Q1/tQ2/t:
Q1/tQ2/t=kAΔTπrkAΔT2r=2rπr
- Simplifying this gives:
Q1/tQ2/t=2π
6. Conclusion: The ratio of the heat transferred through a cross-section of the straight rod to that of the semicircular rod is:
Q1/tQ2/t=2π
- For the semicircular rod (Rod 1), if the radius is r, the length L1 is given by the formula for the arc length of a semicircle:
L1=πr
- For the straight rod (Rod 2), the length L2 is simply the diameter of the semicircle:
L2=2r
Qt=kAΔTL
where:
- k is the thermal conductivity,
- A is the cross-sectional area,
- ΔT is the temperature difference,
- L is the length of the rod.
- For the semicircular rod (Rod 1):
Q1t=kAΔTL1=kAΔTπr
- For the straight rod (Rod 2):
Q2t=kAΔTL2=kAΔT2r
- To find the ratio of heat transfer through the two rods, we take the ratio Q1/tQ2/t:
Q1/tQ2/t=kAΔTπrkAΔT2r=2rπr
- Simplifying this gives:
Q1/tQ2/t=2π
Q1/tQ2/t=2π
Topper's Solved these Questions
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER
11 Videos
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - OBJECTIVE II
6 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 2
6 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Question for short Answer
4 Videos
Similar Questions
Two rods (one semi-circular and other straight) of same material and of same cross-sectional area are joined as shown in the figure. The point A and B are maintained at different temperature. Find the ratio of the heat transferred through a cross-section of a semi-circular rod to the heat transferred through a cross section of the straight rod in a given time.

View SolutionFour rods of same material and having the same cross section and length have been joined, as shown. The temperature of the junction of four rods will be :
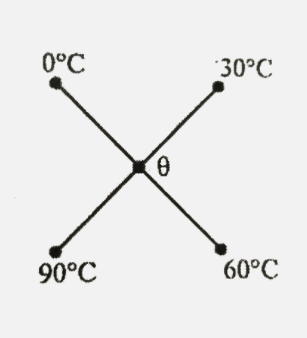
View Solution
Knowledge Check
Heat is flowing through two cylindrical rods of the same material. The diamters of the rods are in the ratio 1:2 and the length in the ratio 2:1. If the temperature difference between the ends is same then ratio of the rate of flow of heat through them will be
A1:1B1:8C2:1D8:1
Three rods made of the same material and having same cross-section area but different length 10 cm, 20 cm and 30 cm are joined as shown. The temperature of the junction is
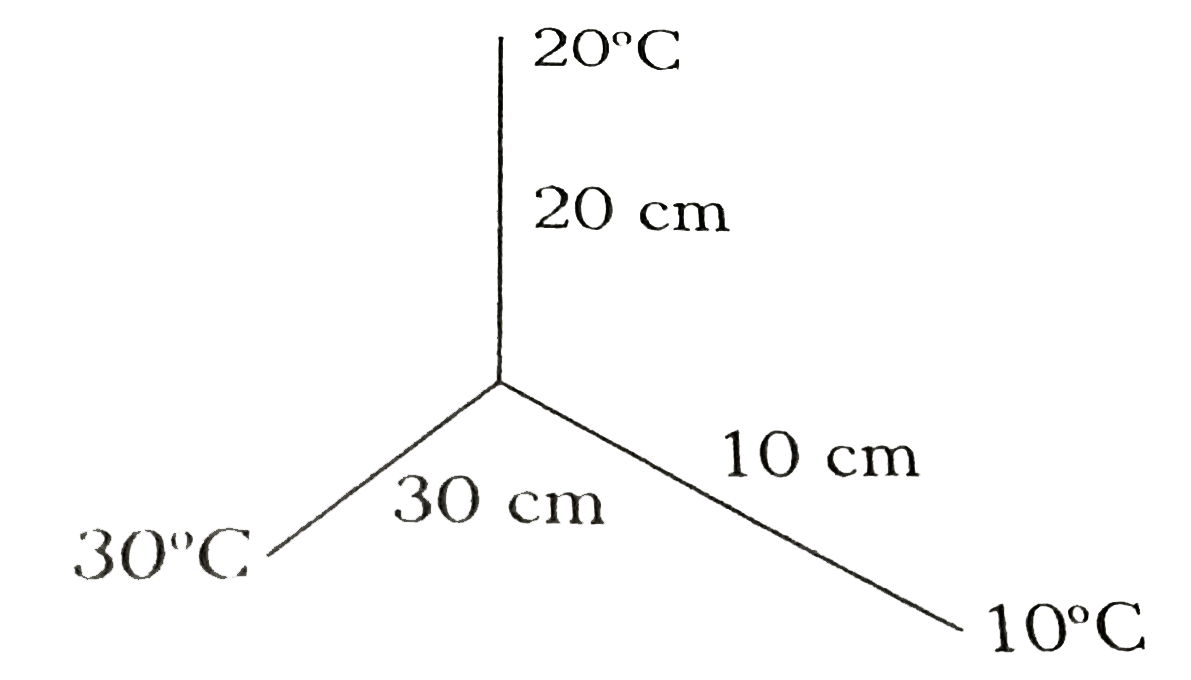
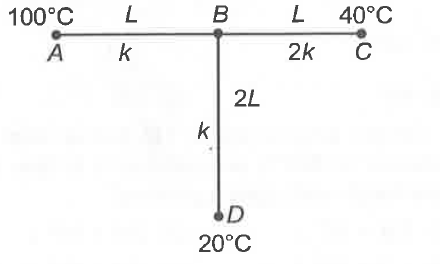
View SolutionFind the temperature of junction at B, if each rod has equal area of cross-section.
View SolutionFive rods of same material and same cross-section are joined as shown. Lengths of rods ab, ad and bc are l, 2l and 3l respectively. Ends a and c are maintained at temperatures 200∘C and 0∘C respectivelly.
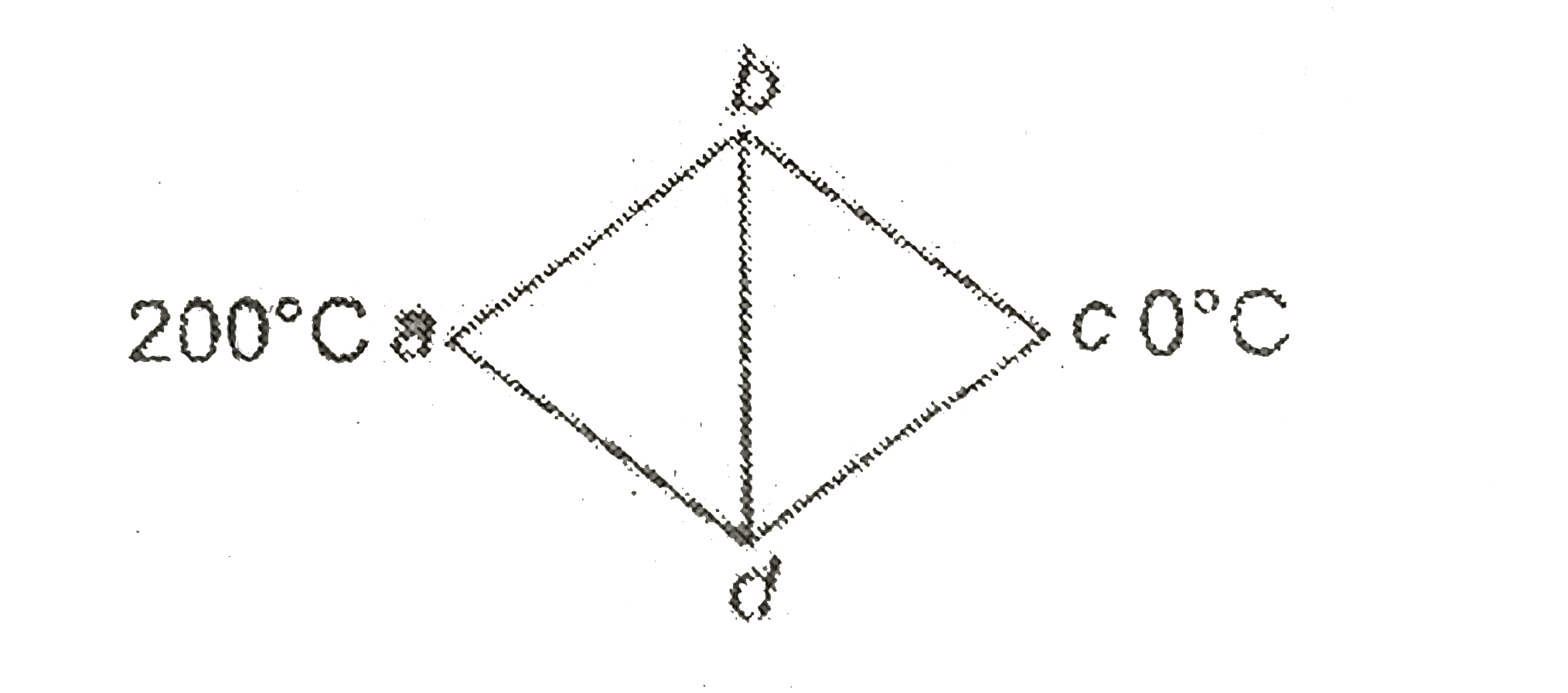
For what length x of rod dc there will be no heat flow through rod bd ?
View SolutionThree rods are made from the same material and having the same cross-sectional area and length have been joined as shown in the figure.
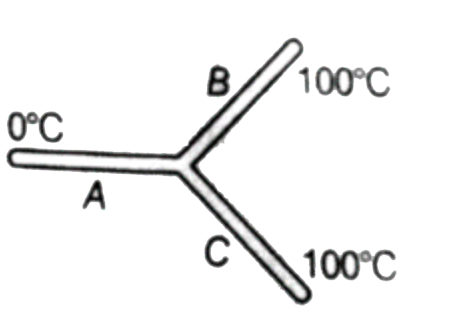
The left end and right end are kept 0∘Cand100∘C , respectively . The temperature of the junction of three rods will be
View SolutionThe end of two rods of different materials with their thermal conductivities, area of cross-section and lengths all in the ratio 1:2 are maintained at the same temperature difference. If the rate of flow of heat in the first rod is 4cal/s. Then, in the second rod rate of heat flow in cal/s will be
View SolutionHeat is flowing through two cylindrical rods of the same material . The diameters of the rods are in the ratio 1:2 and the lengths in the ratio 2:1.If the temperature difference between the ends be the same ,then the ratio of the rate of flow if heat through them will be ?
View SolutionThe two ends of a rod of length L and a uniform cross-sectional area A are kept at two temperature T1 and T2 (T1>T2). The rate of heat transfer. dQdt, through the rod in a steady state is given by
View Solution
