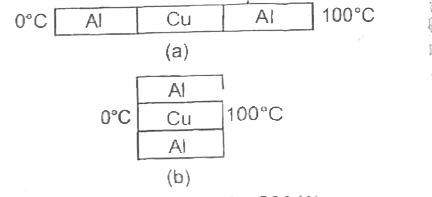
The three rods shown in figure have identical dimensions. Heat flows from the hot end at a rate of 40 W in the arrangement (a). Find the rates of heat flow when the rods are joined as in arrangement (b). (Assume kAl=200Wm∘C and KCu=400Wm∘C
The correct Answer is:D
θ1=θ2=100
QT=Ka(θ1−θ2)t
R=R1+R2+R3 ltbrge =1/(ak_Al)+1/(ak_cu)+1/(ak_Al)<br>=1/a((2/200)+(1/400))<br>1/a((4+1)/400)=1/a 5/400<br>=1/a 1/80<br>Q/t=100/((1/a) (1/80))[:' Q/t=(theta_1-theta_2)/R]<br>40=80xx100xx(a/l)<br>[from question Q/t =40 W.]<br>a/l=1/200<br>for, B R=R1+R2+R3
=RAl+RCuRAlRCu+RAl)
=1aKAl+1aKCu.1aKAl1aKCu.1aKAl
=1aKAl+la(Kal+aKCu)
=1a(1200+1200+400)
=1a(1200+1600)
=1/a((3+1)/(600))=(4/600).(l/a)<br>(Q/t)=(theta_1-theta_2)/R=(100)/((l/4) (4/600))<br>=(600xx100)/4xx(a/l)<br>=(300/4)=75[Using (a/l)=1/200)]<br>For C (1/R)=(1/R_1)+(1/R_1)+(1/R_1)<br>=(1//l)/(ak_(Al))+(1//l)/(ak_(Cu))+(1//l)/(ak_(Al))<br>=(K_(Al)+K_(Cu)+K_(Al)).(a/l)<br>=(2xx200xx400)(a/l)<br>=(a/l)(800)<br>implies R=(a/l)(1/800)<br>(Q/t)=(theta_1-theta_2)/R=(100)/((l/a)(1/800))<br>=(100xx800xxa)/l<br>=(100xx800)/200=400W.



Topper's Solved these Questions
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER
11 Videos
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - OBJECTIVE II
6 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 2
6 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Question for short Answer
4 Videos
Similar Questions
The two rods show in figure have identical geometrical dimension.. They are in contact with two heat baths at temperature 100∘C . And 0∘C . The temperature of the junction is 70∘C . Find the temperature of the junction if the rods are interchanged.

View Solution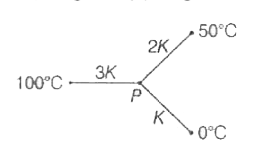
Three rods of the same dimension have thermal conductivity 3K , 2K and K. They are arranged as shown in the figure below
Then , the temperature of the junction in steady - state is
View SolutionAn aluminium rod and copper rod of equal length 1m and cross-sectional area 1cm2 are welded as shown. KA1=200W/m∘C,KCu=400W/m∘C. Find heat current


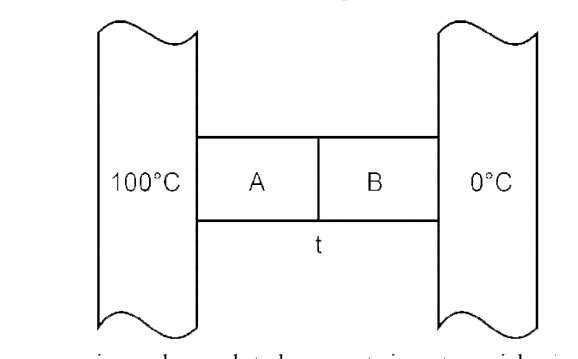
View SolutionTwo metal cubes A and B of same size are arranged as shown in Figure. The extreme ends of the combination are maintained at the indicated temperatures. The arrangement is thermally insulated. The coefficients of thermal conductivity of A and B are 300W/m∘Cand200W/m∘C, respectively. After steady state is reached the temperature t of the interface will be ......
View SolutionA metal ball of mass 2kg is heated means of a 40W heater in a room at 25∘C. The temperature of the ball beomes steady at 60∘C.
Find the rate of loss of heat to the surrounding when the ball is at 60∘C.
View SolutionA metal ball of mass 2kg is heated means of a 40W heater in a room at 25∘C. The temperature of the ball becomes steady at 60∘C.
Find the rate of loss of heat to the surrounding when the ball is at 39∘C.
View SolutionFigure shows a steel rod joined to a brass rod. Each of the rods has length of 31cm and area of cross-section 0.20cm2. The junction is maintained at a constant temperature 50∘C and the two ends are maintained at 100∘C. The amount of heat taken out from the cold junction in 10 minutes after the steady state is reached in n×102J. Find 'n' the thermal conductivities are Ksteel=46W/m−∘C and Kbrass=109W/m−∘C.

View SolutionFigure shows an aluminium rod joined to a copper rod. Each of the rods has a length of 20cm and area of cross section 0.20cm2 . The junction is maintained at a constant temperature 40∘C and the two ends are maintained at 80∘C . Calculate the amount of heat taken out from the cold junction in one minute after the steady state is reached. The conductivities are KAl=200Wm−1C−1 . and KCu=400Wm−1C−1 .

View SolutionA rod of length 1 m is released from rest as shown in the figure below: If ω of rod is √n at the moment it hits the ground, then find n.
View SolutionRate of heat flow through two conducting rods of identical dimensions having thermal conductivities K1 and K2 and Q1 and Q2 when their ends are maintained at the same difference of temperature individually. When the two rods are joined in series with their ends maintained at the same temperature difference (as shown in the figure), the rate of heat flow will be

View Solution