One end of a steel rod (K=46Js−1m−1C−1) of length 1.0m is kept in ice at 0∘C and the other end is kept in boiling water at 100∘C . The area of cross section of the rod is 0.04cm2 . Assuming no heat loss to the atmosphere, find the mass of the ice melting per second. Latent heat of fusion of ice =3.36×105Jkg−1 .
The correct Answer is:A
To solve the problem of finding the mass of ice melting per second when one end of a steel rod is kept in ice at 0°C and the other end in boiling water at 100°C, we can follow these steps:
Step 1: Understand the Heat Transfer Equation
The heat conducted through the rod can be calculated using the formula:
Q=K⋅A⋅(T1−T2)L
where:
- Q = heat transfer per second (in Joules per second or Watts)
- K = thermal conductivity of the material (in Js−1m−1C−1)
- A = cross-sectional area of the rod (in m2)
- T1 = temperature at one end (in °C)
- T2 = temperature at the other end (in °C)
- L = length of the rod (in meters)
Step 2: Convert Units
Convert the area from cm² to m²:
A=0.04cm2=0.04×10−4m2=4×10−6m2
Step 3: Substitute Values into the Heat Transfer Equation
Substituting the known values into the equation:
- K=46Js−1m−1C−1
- A=4×10−6m2
- T1=100°C
- T2=0°C
- L=1m
The heat transfer per second Q is:
Q=46⋅(4×10−6)⋅(100−0)1
Q=46⋅(4×10−6)⋅100
Q=46⋅4×10−4=184×10−4=1.84×10−2J/s
Step 4: Relate Heat Transfer to Ice Melting
The heat required to melt ice can be expressed as:
Q=˙m⋅Lf
where:
- ˙m = mass of ice melting per second (in kg/s)
- Lf = latent heat of fusion of ice (in J/kg)
Given Lf=3.36×105J/kg, we can rearrange the equation to find ˙m:
˙m=QLf
Step 5: Substitute Q and Calculate ˙m
Substituting the values:
˙m=1.84×10−23.36×105
˙m=1.84×10−23.36×105≈5.47×10−8kg/s
Step 6: Convert to Grams
To convert the mass from kg/s to grams/s:
˙m=5.47×10−8kg/s×1000g/kg=5.47×10−5g/s
Final Answer
The mass of ice melting per second is approximately:
˙m≈5.47×10−5g/s
---
The heat conducted through the rod can be calculated using the formula:
Q=K⋅A⋅(T1−T2)L
where:
- Q = heat transfer per second (in Joules per second or Watts)
- K = thermal conductivity of the material (in Js−1m−1C−1)
- A = cross-sectional area of the rod (in m2)
- T1 = temperature at one end (in °C)
- T2 = temperature at the other end (in °C)
- L = length of the rod (in meters)
Convert the area from cm² to m²:
A=0.04cm2=0.04×10−4m2=4×10−6m2
Substituting the known values into the equation:
- K=46Js−1m−1C−1
- A=4×10−6m2
- T1=100°C
- T2=0°C
- L=1m
Q=46⋅(4×10−6)⋅(100−0)1
Q=46⋅(4×10−6)⋅100
Q=46⋅4×10−4=184×10−4=1.84×10−2J/s
The heat required to melt ice can be expressed as:
Q=˙m⋅Lf
where:
- ˙m = mass of ice melting per second (in kg/s)
- Lf = latent heat of fusion of ice (in J/kg)
˙m=QLf
Substituting the values:
˙m=1.84×10−23.36×105
˙m=1.84×10−23.36×105≈5.47×10−8kg/s
To convert the mass from kg/s to grams/s:
˙m=5.47×10−8kg/s×1000g/kg=5.47×10−5g/s
The mass of ice melting per second is approximately:
˙m≈5.47×10−5g/s
Topper's Solved these Questions
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER
11 Videos
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - OBJECTIVE II
6 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 2
6 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Question for short Answer
4 Videos
Similar Questions
One end of conducting rod is maintained at temperature 50∘C and at the other end ice is melting at 0∘C. The rate of melting of ice is doubled if:
View SolutionOne end of a brass rod of length 2.0 m and cross section 1cm2 is kept in steam at 100∘C and the other end in ice at 0∘C. The lateral surface of the rod is covered by heat insulator. Determine the amount of ice melting per minute. Thermal conductivity of brass is 110W/m−K and specific latent heat of fusion of ice is 80cal/g.
View Solution
Knowledge Check
If 10 g of ice is added to 40 g of water at 15∘C, then the temperature of the mixture is (specific heat of water =4.2×103jkg−1K−1, Latent heat of fusion of ice =3.36×105jkg−1)
A15∘CB12∘CC102CD0∘C
An icebox almost completely filled with ice at 0∘C is dipped into a large volume of water at 20∘C . The box has walls of surface area 2400cm2 thickness 2.0mm and thermal conductivity 0.06Wm−1C−1 . Calculate the rate at which the ice melts in the box. Latent heat of fusion of ice =3.4×105Jkg−1 .
View Solution40 g of ice at 0∘C is used to bring down the temperature of a certain mass of water at 60∘C to 10∘С. Find the mass of water used.
[Specific heat capacity of water = 4200 Jkg−1∘C−1]
[Specific latent heat of fusion of ice = 336×103Jkg−1]
View SolutionA metal rod AB of length 10x has its one end A in ice at 0∘C, and the other end B in water at 100∘C. If a point P one the rod is maintained at 400∘C, then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of evaporation of water is 540cal/g and latent heat of melting of ice is 80cal/g. If the point P is at a distance of λx from the ice end A, find the value λ. [Neglect any heat loss to the surrounding.]
View SolutionA copper rod of length 60 cm long and 8 mm in radius is taken and its one end is kept in boiling water and the other end in ice at 0∘C. If 72 gm of ice melts in one hour with is the thermal conductivity of copper ? Latent of fusion of ice =336KJ/Kg.
View SolutionA metal rod AB of length 10x has it one end in ice at 0∘C and the other end B in water at 100∘C If a point P on the rod is maintained at 400∘C then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of melting of ice is 80cal/g If the point P is at a distance of λx from the ice end A find the value of λ [neglect any heat loss to the surrounding] .
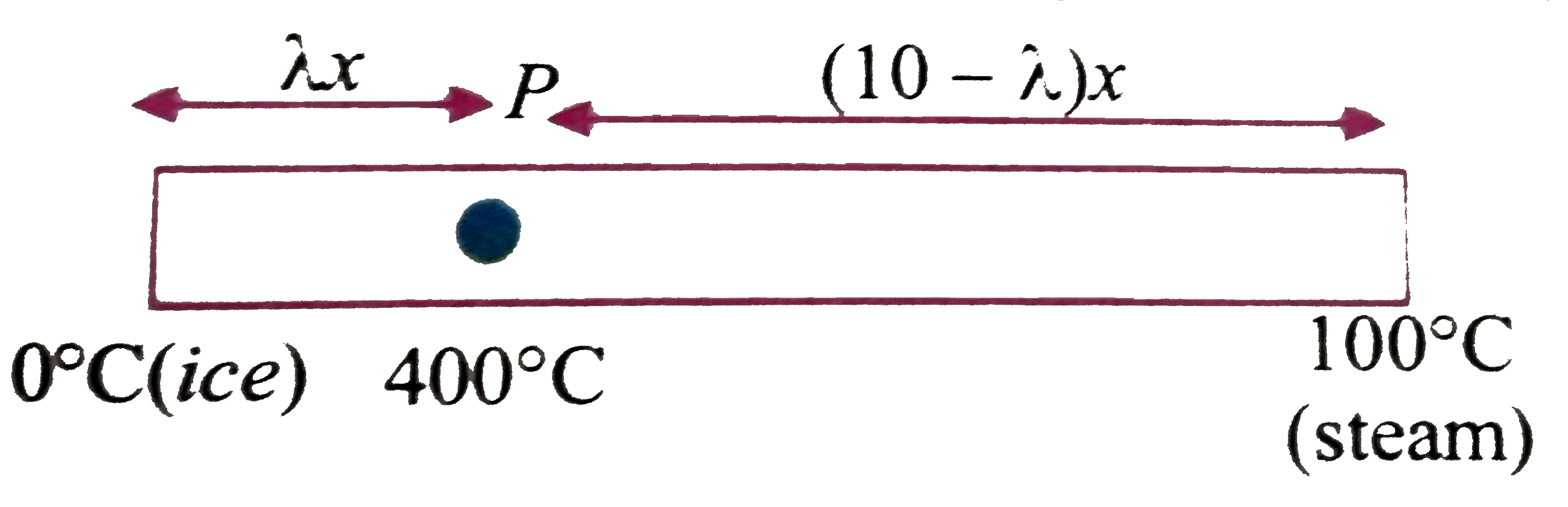 .
.
View SolutionOne end of a copper rod of uniform cross section and length 1.5 m is kept in contact with ice and the other end with water at 100∘C. At what point along its length should a temperature of 200∘C be maintained so that in the steady state, the mass of ice melting be equal to that of the steam produced in same interval of time. Assume that the whole system is insulated from surroundings:
[Lice=80cal/g,Lsteam=540cal/g]
View SolutionOne end of a copper rod of uniform cross section and length 1.5 m is kept in contact with ice and the other end with water at 100∘C. At what point along its length should a temperature of 200∘C be maintained so that in the steady state, the mass of ice melting be equal to that of the steam produced in same interval of time. Assume that the whole system is insulated from surroundings:
[Lice=80cal/g,Lsteam=540cal/g]
View Solution
