A steel frame (K=45Wm−1C−1) of total length 60cm and cross sectional area 0.2cm2 , Forms three side of a square. The free ends are maintained at 20∘C and 40∘C . Find the rate of heat flow through a cross section of the frame.
The correct Answer is:C
To find the rate of heat flow through the cross-section of the steel frame, we can use the formula for heat conduction, which is given by Fourier's law:
Q=K⋅A⋅ΔTL
Where:
- Q = rate of heat flow (in watts)
- K = thermal conductivity of the material (in W/m°C)
- A = cross-sectional area (in m²)
- ΔT = temperature difference (in °C)
- L = length of the material (in meters)
Step 1: Convert the given values to appropriate units
1. Thermal conductivity K: Given as 45W/m°C (no conversion needed).
2. Length L: Given as 60cm. Convert to meters:
L=60cm=0.60m
3. Cross-sectional area A: Given as 0.2cm2. Convert to square meters:
A=0.2cm2=0.2×10−4m2=2×10−5m2
4. Temperature difference ΔT: The temperatures are 40°C and 20°C:
ΔT=40°C−20°C=20°C
Step 2: Substitute the values into the formula
Now we can substitute the values into the formula:
Q=K⋅A⋅ΔTL
Q=45W/m°C⋅2×10−5m2⋅20°C0.60m
Step 3: Calculate the rate of heat flow
Calculating the numerator:
Q=45⋅2×10−5⋅200.60
Q=1800×10−50.60
Q=0.0180.60=0.03W
Final Answer
The rate of heat flow through the cross-section of the frame is:
Q=0.03W
- Q = rate of heat flow (in watts)
- K = thermal conductivity of the material (in W/m°C)
- A = cross-sectional area (in m²)
- ΔT = temperature difference (in °C)
- L = length of the material (in meters)
1. Thermal conductivity K: Given as 45W/m°C (no conversion needed).
2. Length L: Given as 60cm. Convert to meters:
L=60cm=0.60m
3. Cross-sectional area A: Given as 0.2cm2. Convert to square meters:
A=0.2cm2=0.2×10−4m2=2×10−5m2
4. Temperature difference ΔT: The temperatures are 40°C and 20°C:
ΔT=40°C−20°C=20°C
Now we can substitute the values into the formula:
Q=K⋅A⋅ΔTL
Q=45W/m°C⋅2×10−5m2⋅20°C0.60m
Calculating the numerator:
Q=45⋅2×10−5⋅200.60
Q=1800×10−50.60
Q=0.0180.60=0.03W
The rate of heat flow through the cross-section of the frame is:
Q=0.03W
Topper's Solved these Questions
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER
11 Videos
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - OBJECTIVE II
6 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 2
6 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Question for short Answer
4 Videos
Similar Questions
The current density at a point is→j = (2×104ˆj)Jm−2. Find the rate of charge flow through a cross sectional area →S = (2ˆi+3ˆj)cm2
View SolutionTwo parallel plates A and B are joined together to form a compound plate . The thicknesses of the plate are 4.0cm and 2.5cm respectively and the area of cross section is 100cm2 for each plate. The thermal conductivities are KA=200Wm−1C−1 for plate A and KB=400Wm−1C−1 for the plate B. The outer surface of the plate A is maintained at100∘C and the outer surface of the plate B is maintained at 0∘C. Find (a) the rate of heat flow through any cross section, (b) the temperature at the interface and (c) the equivalent thermal conductivity of the compound plate.

View SolutionA metal rod of length 2 m has cross sectional areas 2 A and A as shown in figure. The ends are maintained at temperatures 100° C and 70° C . The temperature at middle point C is

View SolutionThree copper rods and three steel rods each of length l=10cm and area of cross-section 1cm2 are connected as shown

If ends A and E are maintained at temperatures 125∘C and 0∘C respectively, calculate the amount of heat flowing per second from the hot of cold function. [KCu=400W/m−K,Ksteel=50W/m−K]
View SolutionAn aluminium rod and a copper rod of equal length 1.0m and cross-sectional area. 1cm2 are welded together as shown in figure. One end is kept at a temperature of 20∘C and the other at 60∘C Calculate the amount of heat taken out per second from the hot end. thermal conductivity of aluminium =200Wm−1C−1 and of copper =390Wm−1C−1 .

View SolutionFigure shows an aluminium rod joined to a copper rod. Each of the rods has a length of 20cm and area of cross section 0.20cm2 . The junction is maintained at a constant temperature 40∘C and the two ends are maintained at 80∘C . Calculate the amount of heat taken out from the cold junction in one minute after the steady state is reached. The conductivities are KAl=200Wm−1C−1 . and KCu=400Wm−1C−1 .

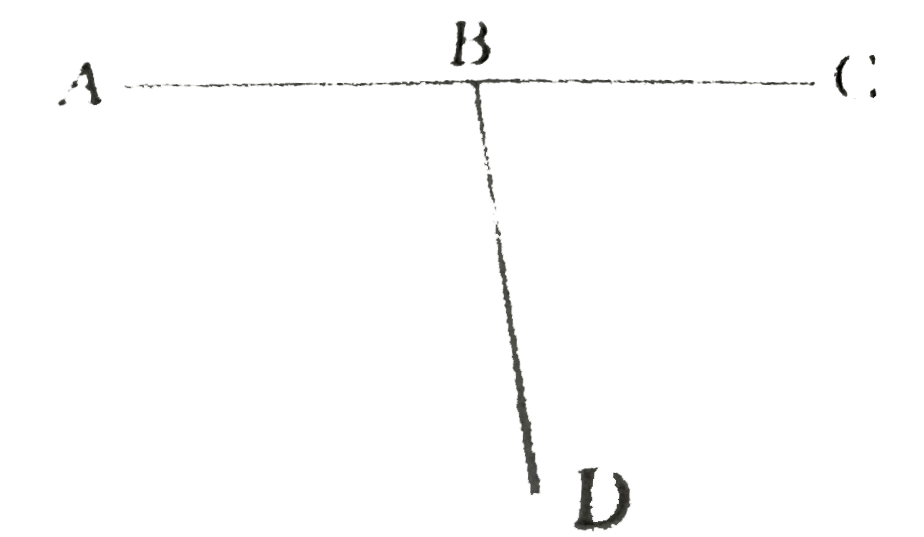
View SolutionThree conducting rods of same material and cross-section are shown in figure. Temperatures of A,D and C are maintained at 20∘C,90∘Cand0∘C. The ratio of lengths BD and BC if there is no heat flow in AB is
View SolutionThe ends of copper rod of length 1m and area of cross section 1cm2 are maintained at 0∘C and 100∘C. At the centre of rod, there is a source of heat of 32W. The thermal conductivity of copper is 400W/mK

View SolutionA bar of copper of length 75cm and a bar of steel of length 125cm are joined together end to end. Both are of circular cross section with diameter 2cm. The free ends of the copper and the steel bars are maintained at 100∘C and 0∘C respectively. The curved surface of the bars are thermally insulated. What is the temperature of the copper-steel junction? What is the amount of heat transmitted per unit time across the junction? Thermal conductivity of copper is 386Js−1m−1C−1 and that of steel is 46Js−1m−1C−1
View SolutionAn aluminium rod and copper rod of equal length 1m and cross-sectional area 1cm2 are welded as shown. KA1=200W/m∘C,KCu=400W/m∘C. Find heat current


View Solution
