Question

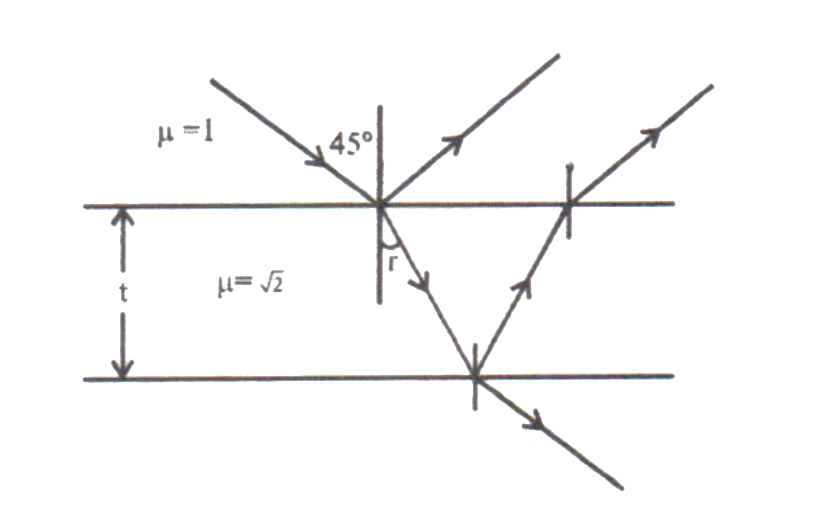
A light ray is incident at an angle of ${45}^{\circ }$ with the normal to a $\sqrt{2}$ cm thick plate$(\mu =2.0)$. Find the shift in the path of the light as it emerges out from the plate.

Answer

B::C

Explanation

To find the shift in the path of light as it emerges from a plate, we can follow these steps:

Step 1: Identify the Given Values
- Angle of incidence (I) = 45°
- Thickness of the plate (T) = √2 cm
- Refractive index of the plate (μ) = 2.0
- Refractive index of air (n1) = 1.0

Step 2: Use Snell's Law to Find the Angle of Refraction (R)
Using Snell's Law:
\( n_1 \sin I = n_2 \sin R \)
Substituting the known values:
\( 1 \cdot \sin(45°) = 2 \cdot \sin R \)
Since \(\sin(45°) = \frac{1}{\sqrt{2}}\), we have:
\( \frac{1}{\sqrt{2}} = 2 \cdot \sin R \)
Solving for \(\sin R\):
\( \sin R = \frac{1}{2\sqrt{2}} = \frac{1}{2\sqrt{2}} \approx 0.3536 \)
Now, we can find the angle R:
\( R \approx 20.7° \)

Step 3: Calculate the Lateral Displacement (Δ)
The formula for lateral displacement (Δ) is given by:
\( \Delta = T \cdot \frac{\sin(I - R)}{\cos R} \)
Substituting the values we have:
- \(T = \sqrt{2} \text{ cm}\)
- \(I = 45°\)
- \(R \approx 20.7°\)

Calculating \(I - R\):
\( I - R = 45° - 20.7° = 24.3° \)

Now substituting into the formula:
\( \Delta = \sqrt{2} \cdot \frac{\sin(24.3°)}{\cos(20.7°)} \)

Step 4: Calculate \(\sin(24.3°)\) and \(\cos(20.7°)\)
Using a calculator:
- \(\sin(24.3°) \approx 0.409\)
- \(\cos(20.7°) \approx 0.935\)

Step 5: Substitute and Solve
Now substituting these values into the equation:
\( \Delta = \sqrt{2} \cdot \frac{0.409}{0.935} \)
Calculating:
\( \Delta \approx 1.414 \cdot 0.438 \approx 0.620 \text{ cm} \)

Final Result
Thus, the shift in the path of light as it emerges from the plate is approximately:
\( \Delta \approx 0.622 \text{ cm} \)