A narrow pencil of parallel light is incident normally on a solid transparent sphere of radius r. What should be the refractive index if the pencil is to be focussed (a) at the surface of the sphere, (b) at the centre of the sphere.
The correct Answer is:A, B, C, D
To solve the problem, we need to determine the refractive index of a solid transparent sphere when a narrow pencil of parallel light is incident normally on its surface. We will consider two cases: (a) when the light is focused at the surface of the sphere and (b) when the light is focused at the center of the sphere.
Given:
- Radius of the sphere, r
- Refractive index of air, μ1=1
- Object distance, u=−∞ (since the light rays are coming from infinity)
Case (a): Focusing at the Surface of the Sphere
1. Identify the Image Distance:
- Since the light is focused at the surface of the sphere, the image distance v=2r (the distance from the center of the sphere to the surface is r, and the light converges to the surface).
2. Apply the Lens Maker's Formula:
The formula for refraction at a curved surface is given by:
μ2v−μ1u=μ2−μ1R
Here, R=r (the radius of the sphere).
3. Substituting Values:
Substitute v=2r, u=−∞, and R=r:
μ22r−1−∞=μ2−1r
The term 1−∞ becomes 0, so we have:
μ22r=μ2−1r
4. Simplifying the Equation:
Multiply through by 2r:
μ2=2(μ2−1)
Expanding gives:
μ2=2μ2−2
Rearranging leads to:
μ2−2μ2=−2⟹−μ2=−2⟹μ2=2
Conclusion for Case (a):
The refractive index μ2 for the light to be focused at the surface of the sphere is 2.
---
Case (b): Focusing at the Center of the Sphere
1. Identify the Image Distance:
- For this case, the image is formed at the center of the sphere, so the image distance v=r.
2. Apply the Lens Maker's Formula Again:
Using the same formula:
μ2v−μ1u=μ2−μ1R
Substitute v=r, u=−∞, and R=r:
μ2r−1−∞=μ2−1r
Again, the term 1−∞ becomes 0:
μ2r=μ2−1r
3. Simplifying the Equation:
Multiply through by r:
μ2=μ2−1
Rearranging gives:
0=−1
This is not possible.
Conclusion for Case (b):
The equation cannot be satisfied, indicating that it is not possible for the light to be focused at the center of the sphere.
---
Summary of Results:
- (a) The refractive index μ2 for focusing at the surface of the sphere is 2.
- (b) It is not possible to focus the light at the center of the sphere.
- Radius of the sphere, r
- Refractive index of air, μ1=1
- Object distance, u=−∞ (since the light rays are coming from infinity)
1. Identify the Image Distance:
- Since the light is focused at the surface of the sphere, the image distance v=2r (the distance from the center of the sphere to the surface is r, and the light converges to the surface).
The formula for refraction at a curved surface is given by:
μ2v−μ1u=μ2−μ1R
Here, R=r (the radius of the sphere).
Substitute v=2r, u=−∞, and R=r:
μ22r−1−∞=μ2−1r
The term 1−∞ becomes 0, so we have:
μ22r=μ2−1r
Multiply through by 2r:
μ2=2(μ2−1)
Expanding gives:
μ2=2μ2−2
Rearranging leads to:
μ2−2μ2=−2⟹−μ2=−2⟹μ2=2
The refractive index μ2 for the light to be focused at the surface of the sphere is 2.
1. Identify the Image Distance:
- For this case, the image is formed at the center of the sphere, so the image distance v=r.
Using the same formula:
μ2v−μ1u=μ2−μ1R
Substitute v=r, u=−∞, and R=r:
μ2r−1−∞=μ2−1r
Again, the term 1−∞ becomes 0:
μ2r=μ2−1r
Multiply through by r:
μ2=μ2−1
Rearranging gives:
0=−1
This is not possible.
The equation cannot be satisfied, indicating that it is not possible for the light to be focused at the center of the sphere.
- (a) The refractive index μ2 for focusing at the surface of the sphere is 2.
- (b) It is not possible to focus the light at the center of the sphere.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXAMPLE
9 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -2
7 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
Similar Questions
A parallel beam of light falls on a solid tranparent sphere.
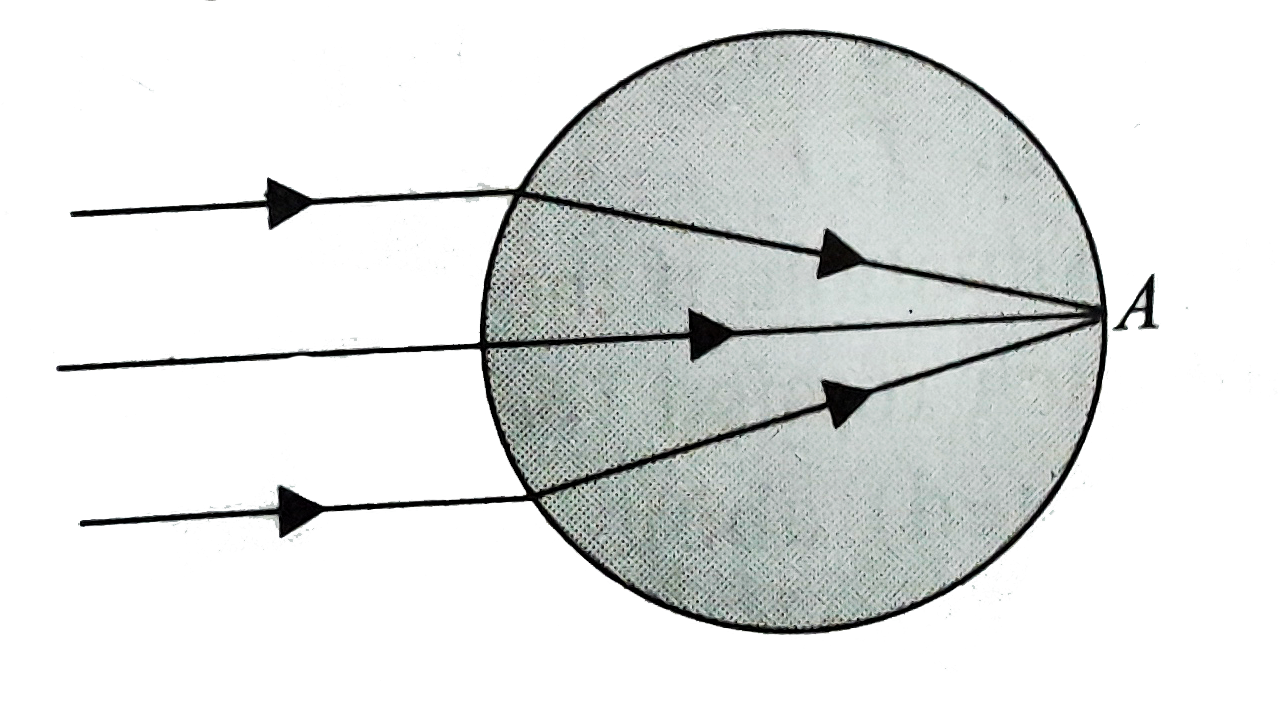
Q. Which is corret?
View SolutionA parallel beam of light falls on a solid tranparent sphere.
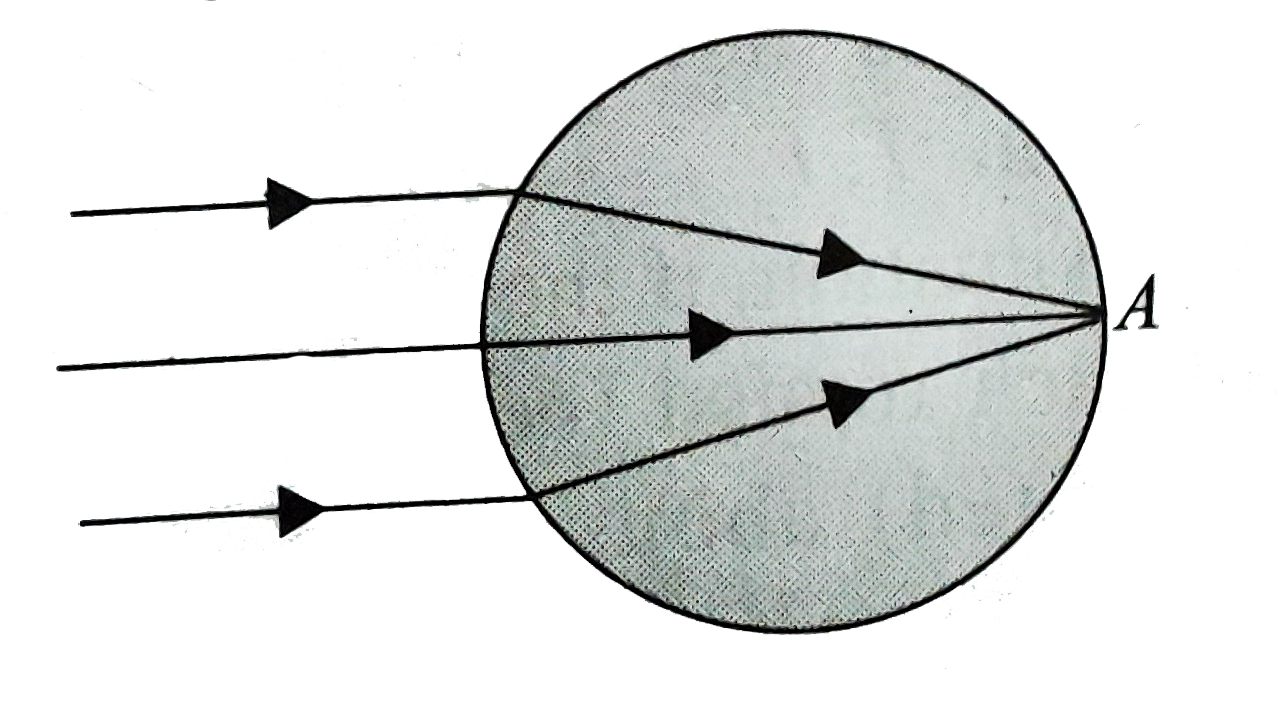
Q. For what value of refractive index μ, the thin beam can be focussed at centre of sphere.
View SolutionA narrow parallel beam of light is incident on a transparent sphere of refractive index n if the beam finally gets focused at a point situated at a distance=2×(radius of sphere) form the center of the sphere then find n?
View SolutionA parallel beam of light falls on a solid tranparent sphere.
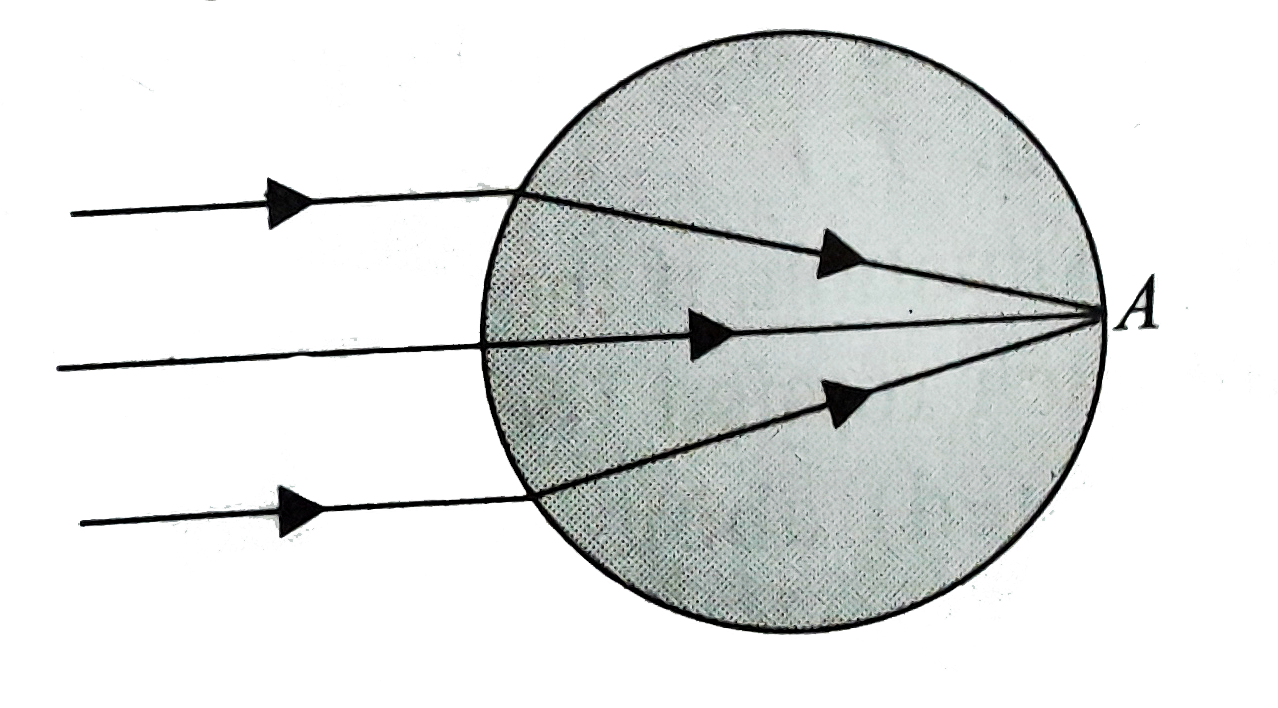
Q. If however thin beam is focussed at A, then find the refractive index of the sphere,
View SolutionA horizontal ray of light is incident on a solid glass sphere of radius R and refractive index μ . What is net deviation of the beam when it emerged from the other side of the sphere?
View SolutionA ray of light is incident on a glass sphere of refractive index 3/2. What should be the angle of incidence so that the ray which enters the sphere does not come out of the sphere ?
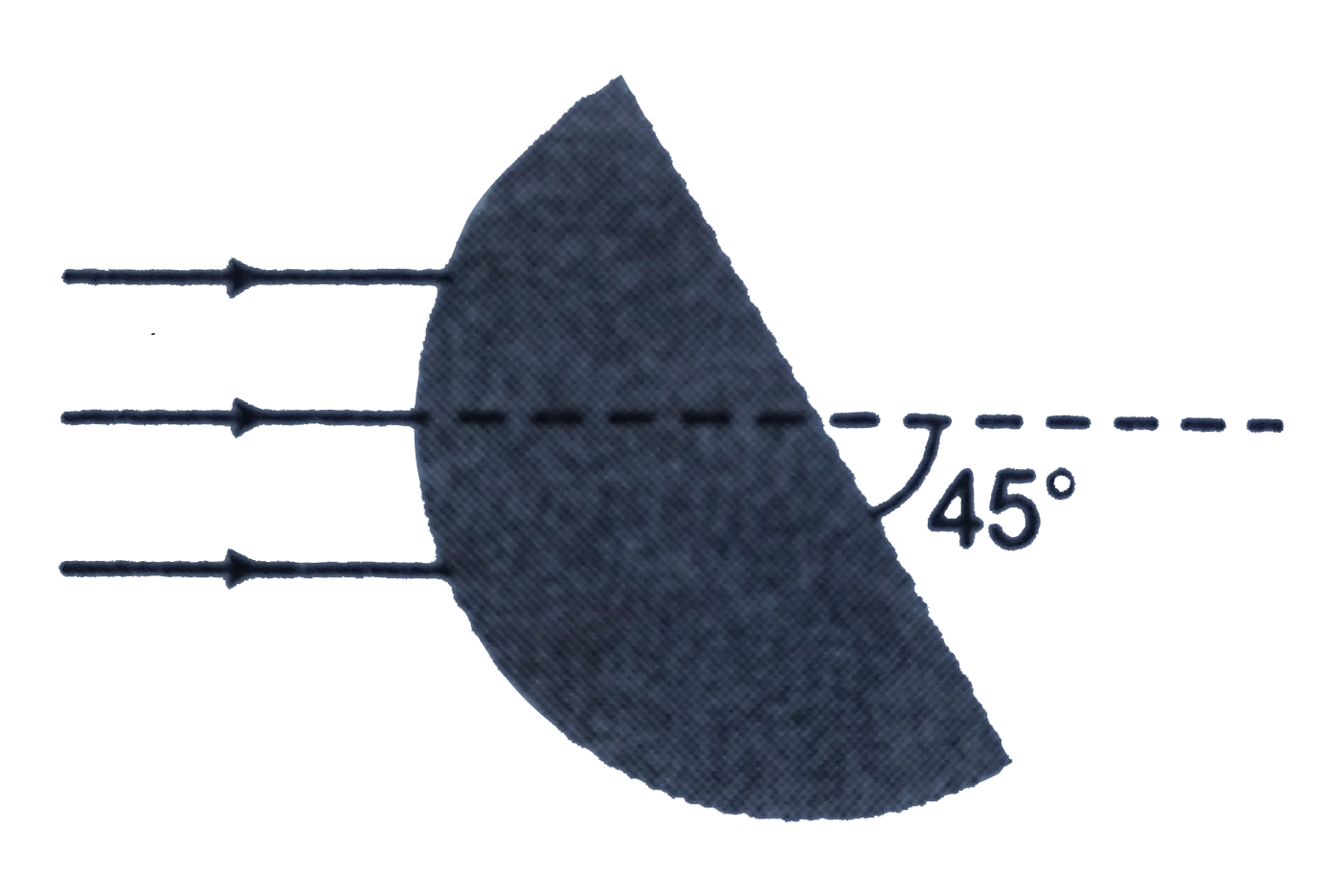
View SolutionA parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index μ=1.5 as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as
View SolutionA sphere of radius R rolls without slipping between two planks as shown in figure. Find
(a) Speed of centre of sphere
(b) Angular velocity of the sphere
View SolutionA parallel beam falls on solid glass sphere of radius R and refractive index μ. What is the distance of final image after refractioin from two surfaces of sphere? What is the condition for the image to be real?
View SolutionA parallel beam of light emerges from the opposite surface of the sphere when a point source of light lies at the surface of the sphere. The refractive index of the sphere is
View Solution
