A biconvex thick lens is constructed with glass (mu = 1.50). Each of the surfaces has a radius of 10 cm and the thickness at the middle is 5 cm. Locate the image of an object placed far away from the lens.
The correct Answer is:A, C, D
To locate the image formed by a biconvex thick lens, we can follow these steps:
Step 1: Identify the parameters of the lens
- The lens is biconvex with a refractive index (μ) of 1.50.
- The radius of curvature for both surfaces (R1 and R2) is 10 cm.
- The thickness of the lens at the center is 5 cm.
Step 2: Determine the object distance for the first surface
Since the object is placed far away from the lens, we can consider the object distance (U) to be infinity (U = ∞).
Step 3: Apply the lens maker's formula for the first surface
Using the refraction formula at the first surface (Surface 1):
μ2V−μ1U=μ2−μ1R
Where:
- μ2 = 1.5 (glass)
- μ1 = 1 (air)
- R1 = +10 cm (since it is convex)
Substituting the values:
1.5V−1∞=1.5−110
This simplifies to:
1.5V=0.510
1.5V=0.05
V=1.50.05=30 cm
So, the image formed by the first surface is at 30 cm from the first surface.
Step 4: Determine the object distance for the second surface
The image formed by the first surface acts as the object for the second surface. The distance from the first surface to the second surface is the thickness of the lens (5 cm). Therefore, the object distance for the second surface (U2) is:
U2=30 cm−5 cm=25 cm
Step 5: Apply the lens maker's formula for the second surface
Using the refraction formula at the second surface (Surface 2):
μ2V−μ1U=μ2−μ1R
Where:
- μ2 = 1 (air)
- μ1 = 1.5 (glass)
- R2 = -10 cm (since it is convex but we take it as negative for the second surface)
Substituting the values:
1V−1.525=1−1.5−10
This simplifies to:
1V−1.525=−0.5−10
1V−1.525=0.05
Now, we can solve for V:
1V=0.05+1.525
Calculating 1.525:
1.525=0.06
Thus,
1V=0.05+0.06=0.11
So,
V=10.11≈9.09 cm
Step 6: Conclusion
The final image is formed approximately 9.1 cm from the second surface of the lens.
---
- The lens is biconvex with a refractive index (μ) of 1.50.
- The radius of curvature for both surfaces (R1 and R2) is 10 cm.
- The thickness of the lens at the center is 5 cm.
Since the object is placed far away from the lens, we can consider the object distance (U) to be infinity (U = ∞).
Using the refraction formula at the first surface (Surface 1):
μ2V−μ1U=μ2−μ1R
Where:
- μ2 = 1.5 (glass)
- μ1 = 1 (air)
- R1 = +10 cm (since it is convex)
1.5V−1∞=1.5−110
This simplifies to:
1.5V=0.510
1.5V=0.05
V=1.50.05=30 cm
So, the image formed by the first surface is at 30 cm from the first surface.
The image formed by the first surface acts as the object for the second surface. The distance from the first surface to the second surface is the thickness of the lens (5 cm). Therefore, the object distance for the second surface (U2) is:
U2=30 cm−5 cm=25 cm
Using the refraction formula at the second surface (Surface 2):
μ2V−μ1U=μ2−μ1R
Where:
- μ2 = 1 (air)
- μ1 = 1.5 (glass)
- R2 = -10 cm (since it is convex but we take it as negative for the second surface)
1V−1.525=1−1.5−10
This simplifies to:
1V−1.525=−0.5−10
1V−1.525=0.05
Now, we can solve for V:
1V=0.05+1.525
Calculating 1.525:
1.525=0.06
Thus,
1V=0.05+0.06=0.11
So,
V=10.11≈9.09 cm
The final image is formed approximately 9.1 cm from the second surface of the lens.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXAMPLE
9 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -2
7 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
Similar Questions
A convex lens of focal length 10 cm is painted black at the middle portion as shown in figure. An object placed at a distance of 20 cm from the lens. Then
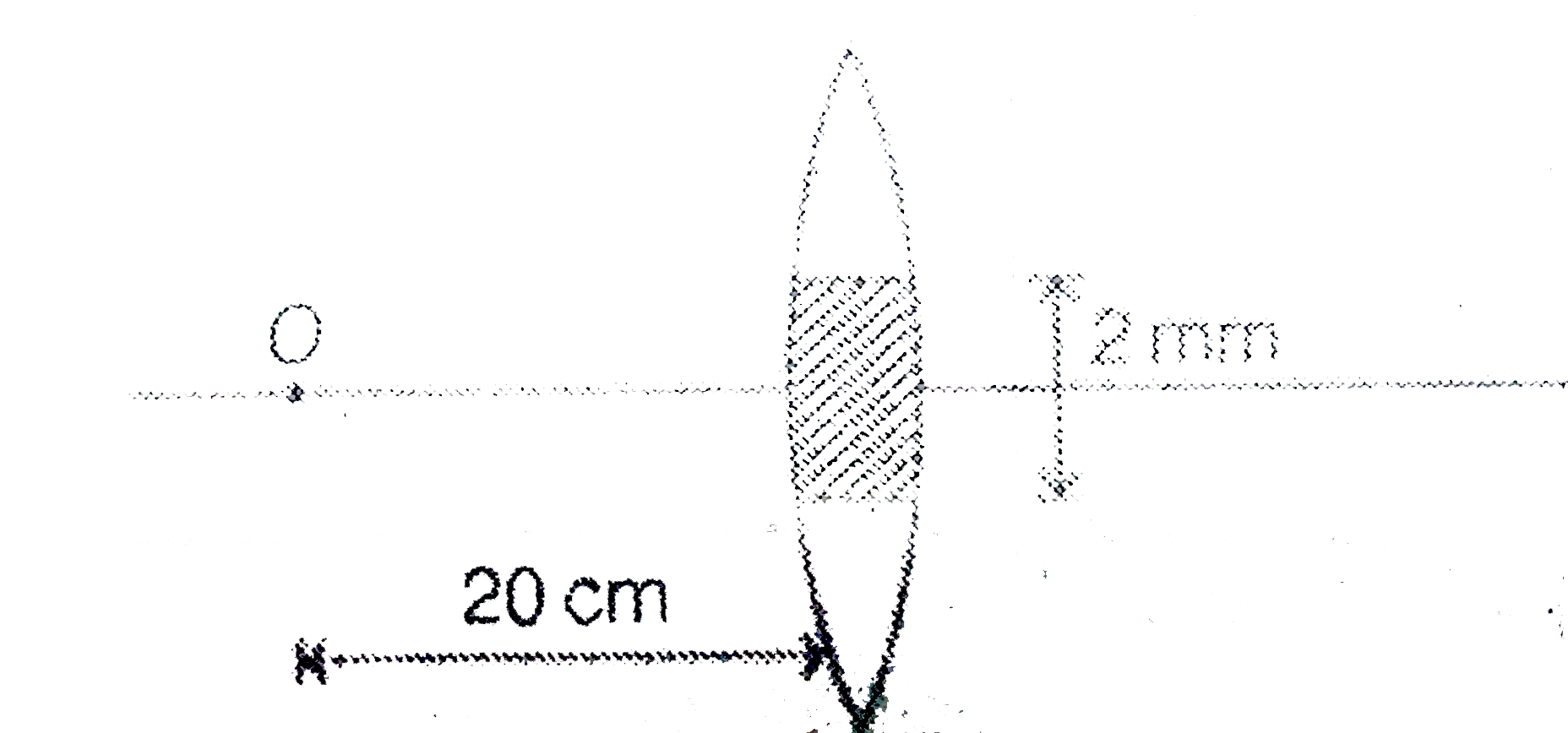
View SolutionA concave convex figure lens made of glas (μ=1.5) has surface of radii 20 cm and 60 cm. a. Locate the image ofan object placed 80 cm to the left of the lens along the principal axis. B. A similar lens is placed coaxially at distanc of 160 cm right of it. Locate the position of the image.

View Solution
Knowledge Check
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirror
A biconvex thin lens is prepared from glass (μ=1.5), the two bounding surfaces having equal radii of 25 cm each. One of the surfaces is silvered from outside to make it reflecting. Whee should an object be placed before this lens so that the image is formed on the object itself?

View SolutionA biconvex thin lens is prepared from glass (μ=1.5), the two bounding surfaces having equal radii of 25 cm each. One of the surfaces is silvered from outside to make it reflecting. Whee should an object be placed before this lens so that the image is formed on the object itself?

View SolutionA convex lens has a focal length of 20 cm. It is used to form an image of an object placed 15 cm from lens. The image is
View SolutionA convexo-convex has a focal length of f1=10cm. One of the lens surfaces having a radius of curvature of R=10cm is coated with silver. Construct the image of the object produced by the given optical system and determine the position of the image if the object is at a distance of a=15cm from the lens. Refractive index of lens =1.5.
View SolutionA biconvex lens has a radius of curvature of magnitude 20cm. Which one of the following options describes best the image formed of an object of height 2cm place 30cm from the lens ?
View SolutionA point object is placed on the principal axis of a convex lens (f = 15 cm) at a distance of 30 cm from it. A glass plate (μ=1.50) of thickness 1 cm is placed on the other side of the lens perpendicular to the axis. Locate the image of the point object.
View SolutionA biconvex thin lens is prepared from glass of refractive index μ2=32. The two conducting surfaces have equal radii of 20 cm each. One of the the surface is silvered from outside to make it reflecting. It is placed in a medium of refractive index μ1=53. It acts as a
View Solution
