A convex lens has a focal length of 20 cm. It is used to form an image of an object placed 15 cm from lens. The image is
virtual inverted and enlarge
real,inverted and diminished
real,inverted and enlarge
virtual,erect and enlarge
The correct Answer is:D
To solve the problem step-by-step, we will use the lens formula and the properties of the image formed by a convex lens.
Step 1: Identify the given values
- Focal length (f) of the convex lens = +20 cm (positive because it is a convex lens)
- Object distance (u) = -15 cm (negative because object distance is measured against the direction of incident light)
Step 2: Use the lens formula
The lens formula for a convex lens is given by:
1f=1v−1u
Where:
- f = focal length
- v = image distance
- u = object distance
Step 3: Substitute the known values into the lens formula
Substituting the values we have into the lens formula:
120=1v−1−15
This simplifies to:
120=1v+115
Step 4: Find a common denominator and solve for v
To solve for v, we first find a common denominator for the fractions on the right side. The common denominator of 20 and 15 is 60.
120=360and115=460
Substituting these into the equation gives:
360=1v+460
Now, rearranging gives:
1v=360−460=−160
Thus,
v=−60cm
Step 5: Determine the properties of the image
1. Nature of the image: Since v is negative, the image is virtual.
2. Orientation of the image: The image formed by a convex lens when the object is between the focal point and the lens is erect.
3. Size of the image: The magnification (m) can be calculated using the formula:
m=−vu
Substituting the values:
m=−−60−15=4
This indicates that the image is enlarged (4 times the size of the object).
Final Conclusion
The image formed is virtual, erect, and enlarged.
Summary of the properties of the image:
- Virtual
- Erect
- Enlarged
- Focal length (f) of the convex lens = +20 cm (positive because it is a convex lens)
- Object distance (u) = -15 cm (negative because object distance is measured against the direction of incident light)
The lens formula for a convex lens is given by:
1f=1v−1u
Where:
- f = focal length
- v = image distance
- u = object distance
Substituting the values we have into the lens formula:
120=1v−1−15
This simplifies to:
120=1v+115
To solve for v, we first find a common denominator for the fractions on the right side. The common denominator of 20 and 15 is 60.
120=360and115=460
Substituting these into the equation gives:
360=1v+460
Now, rearranging gives:
1v=360−460=−160
Thus,
v=−60cm
1. Nature of the image: Since v is negative, the image is virtual.
2. Orientation of the image: The image formed by a convex lens when the object is between the focal point and the lens is erect.
3. Size of the image: The magnification (m) can be calculated using the formula:
m=−vu
Substituting the values:
m=−−60−15=4
This indicates that the image is enlarged (4 times the size of the object).
The image formed is virtual, erect, and enlarged.
- Virtual
- Erect
- Enlarged
Topper's Solved these Questions
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Checkpoint 9.5
Explore 10 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Checkpoint 9.6
Explore 20 Videos
- RAY OPTICSBook:DC PANDEY ENGLISHChapter:RAY OPTICSExercise:Checkpoint 9.3
Explore 20 Videos
- NUCLEIBook:DC PANDEY ENGLISHChapter:NUCLEIExercise:C MADICAL ENTRANCES GALLERY
Explore 46 Videos
- REFLECTION OF LIGHTBook:DC PANDEY ENGLISHChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
Similar Questions
A convex lens has a focal length of 10 cm. Find the location and nature of the image if a point object is placed on the principal axis at a distance of (a) 9.8 cm, (b) 10.2 cm from the lens.
View SolutionA convex lens of focal length 20cm is placed 10cm away from a second convex lens of focal length 25 cm. What wil be the location of the image of an object at 30 cm in front of the first lens?
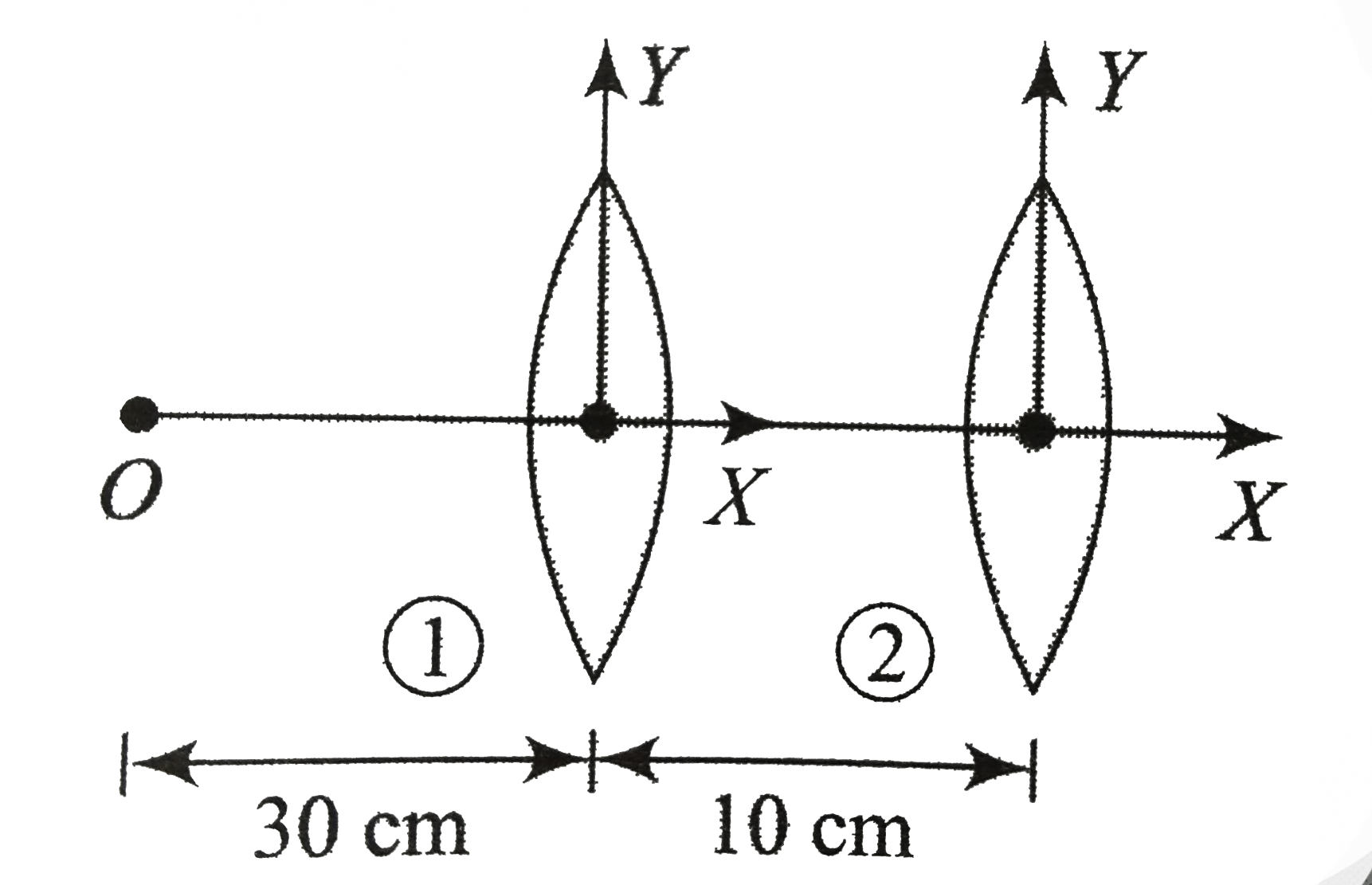
View Solution
Knowledge Check
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirror
An object of length 2.0 cm is placed perpendicular to the principal axis of a convex lens of focal length 12 cm. Find the size of the image of the object is at a distance of 8.0 cm from the lens.
View SolutionA concave lens has focal length of 15 cm. At what distance should an object from the lens be placed so that it forms an image at 10 cm from the lens ? Also, find the magnification of the lens.
View SolutionThe plane surface of a plano-convex lens of focal length 60 cm is silvered. A point object is placed at a distance 20 cm from the lens. Find the position and nature of the final image formed.
View SolutionA thin convex lens of focal length 30cm is placed in front of a plane mirror. An object is placed at a distance x from the lens (not in between lens and mirror ) so that its final image coincides with itself. Then, the value of x is
View SolutionA convex lens of focal length 30 cm forms an image of height 2 cm for an object situated at infinity. If a concave lens of focal length 20 cm is placed coaxially at a distance of 26 cm from convex lens then size of image would be
View SolutionAn object is at a distance of 20 m form a convex lens of focal length 0.3m The lens forms an image of the object moves away form the lens at a speed of 5m/s the speed and direction of the image will be :
View SolutionAn optical system consists of a thin convex lens of focal length 30cm and a plane mirror placed 15cm behind the lens. An object is placed 15cm in front of the lens. The distance of the final image from the object is
View Solution

