The radii of curvature of a lens are + 20 cm and + 30 cm. The material of the lens has a refracting index 1-6. Find the focal length of the lens (a) if it is placed in air, and (b) if it is placed in water (mu = 1.33).
The correct Answer is:A, B, C
To find the focal length of the lens using the lens maker's formula, we will follow these steps:
Given Data:
- Radius of curvature R1=+20cm
- Radius of curvature R2=+30cm
- Refractive index of the lens μl=1.6
- Refractive index of air μm=1
- Refractive index of water μm=1.33
Step 1: Use the Lens Maker's Formula
The lens maker's formula is given by:
1f=(μlμm−1)(1R1−1R2)
Step 2: Calculate the Focal Length in Air
(a) When the lens is placed in air:
1. Substitute the values into the formula:
1f=(1.61−1)(120−130)
2. Simplify the expression:
1f=(1.6−1)(120−130)
=0.6(3−260)=0.6(160)
=0.660=1100
3. Therefore, the focal length f is:
f=100cm
Step 3: Calculate the Focal Length in Water
(b) When the lens is placed in water:
1. Substitute the values into the formula:
1f=(1.61.33−1)(120−130)
2. Simplify the expression:
1f=(1.61.33−1)(120−130)
=(1.202−1)(120−130)
=0.202(120−130)=0.202(3−260)=0.202(160)
=0.20260=1296
3. Therefore, the focal length f is:
f=296cm
Final Answers:
- (a) Focal length in air: f=100cm
- (b) Focal length in water: f=296cm
- Radius of curvature R1=+20cm
- Radius of curvature R2=+30cm
- Refractive index of the lens μl=1.6
- Refractive index of air μm=1
- Refractive index of water μm=1.33
The lens maker's formula is given by:
(a) When the lens is placed in air:
1. Substitute the values into the formula:
1f=(1.61−1)(120−130)
1f=(1.6−1)(120−130)
=0.6(3−260)=0.6(160)
=0.660=1100
f=100cm
(b) When the lens is placed in water:
1. Substitute the values into the formula:
1f=(1.61.33−1)(120−130)
1f=(1.61.33−1)(120−130)
=(1.202−1)(120−130)
=0.202(120−130)=0.202(3−260)=0.202(160)
=0.20260=1296
f=296cm
- (a) Focal length in air: f=100cm
- (b) Focal length in water: f=296cm
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXAMPLE9videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer18videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -27videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question7videos
GAUSS LAW
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
Similar Questions
The radius of curvature of the convex face of a plano convex lens is 12cm and the refractive index of the material of the lends 1.5. Then, the focal length of the lens is
View SolutionThe radii of curvature of the two surfaces of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5. If the lens is concave -convex, then the focal length of the lens is
View Solution
Knowledge Check
- Question 1 - Select One
The radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
Aact as a convex lens only for the objects that lie on its curved side.Bact as a concave lens for the objects that lie on its curved side.Cact as a convex lens irrespective of the side on which the object lies.Dact as a concave lens irrespective of side on which the object lies.
The radii of curvature of the two surfaces of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5. If the lens is concave -convex, then the focal length of the lens is
View SolutionA bicovex lens has radii of cuvature 20 cm each. If the refractive index of the material of the lens is 1.5, what is its focal length?
View SolutionA thin lens made of a material of refractive index μ0 has a focal length f0 in air. Find the focal length of this lens if it is immersed in a liquid of refractive index μ.
View SolutionA plano-convex lens has refractive index 1.6 and radius of curvature 60 cm. What is the focal length of the lens?
View SolutionIf radii of curvature of both convex surfaces is 20 cm, then focal length of the lens for an object placed in air in the given arrangement is
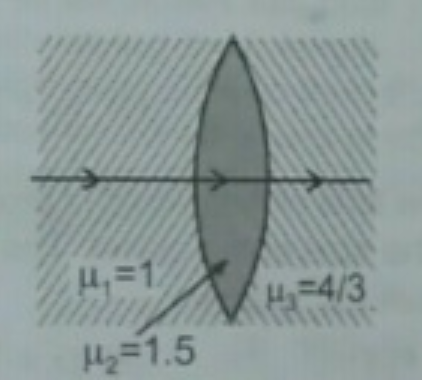 View Solution
View SolutionA diverging meniscus lens of radii of curvatures 25 cm and 50 cm has a refractive index 1.5. Its focal length is (in cm)
View SolutionA biconvex lens has radii of curvature 20 cm and 40cm. The refractive index of the material of the lens is 1.5. An object is placed 40cm in front of the lens. Calculate the psition of the image.
View Solution
