The radius of curvature of the convex face of a plano convex lens is 12cm and the refractive index of the material of the lends 1.5. Then, the focal length of the lens is
6cm
12cm
18cm
24cm
The correct Answer is:D
To find the focal length of a plano-convex lens with a given radius of curvature and refractive index, we can use the lens maker's formula:
1f=(μ−1)(1R1−1R2)
1. Identify the Given Values:
- Refractive index (μ) = 1.5
- Radius of curvature of the convex surface (R1) = 12 cm
- Radius of curvature of the plane surface (R2) = ∞ (infinity)
2. Assign the Values to the Formula:
- Since R2 is infinity, we know that 1R2=0.
- Therefore, the formula simplifies to:
1f=(μ−1)(1R1−0)
3. Substitute the Values into the Equation:
- Substitute μ=1.5 and R1=12 cm into the equation:
1f=(1.5−1)(112)
- This simplifies to:
1f=0.5×112
4. Calculate 1f:
- Multiply the values:
1f=0.512=124
5. Find the Focal Length (f):
- Taking the reciprocal gives us the focal length:
f=24 cm
Final Answer:
The focal length of the lens is 24 cm.
---
- Refractive index (μ) = 1.5
- Radius of curvature of the convex surface (R1) = 12 cm
- Radius of curvature of the plane surface (R2) = ∞ (infinity)
- Since R2 is infinity, we know that 1R2=0.
- Therefore, the formula simplifies to:
1f=(μ−1)(1R1−0)
- Substitute μ=1.5 and R1=12 cm into the equation:
1f=(1.5−1)(112)
- This simplifies to:
1f=0.5×112
- Multiply the values:
1f=0.512=124
- Taking the reciprocal gives us the focal length:
f=24 cm
The focal length of the lens is 24 cm.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - medical entrance special format question
23 Videos
- NUCLEIBOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
The radius of curvature of the convex surface of a thin plano-convex lens is 12 cm, and the refractive index of its material is 1.6. What is the power of lens ?
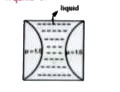
View SolutionThe effective focal length of the lens combination shown in figure is -60 cm. The radius of curvature of the curved surfaces of the plano-convex lenses are 12 cm each and refractive index of the material of the lens is 1.5. The refractive index of the liquid is
View Solution
Knowledge Check
The radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
Aact as a convex lens only for the objects that lie on its curved side.Bact as a concave lens for the objects that lie on its curved side.Cact as a convex lens irrespective of the side on which the object lies.Dact as a concave lens irrespective of side on which the object lies.
The redius of curvature of the convex face of a plano-convex lens is 12cm and its refractive index is 1.5.
a. Find the focal length of this lens. The plane surface of the lens is now silvered.
b. At what distance form the lans will parallel rays incident on the convex face converge?
c. Sketch the ray diagram to locate the image, when a point object is places on the axis 20cm from the lens.
d. Calculate the image distance when the object is placed as in (c).
View SolutionFind the radius of curvature of the convex surface of a plan-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5.
View SolutionThe radius of curvature of curved surface of a thin plano-convex lens is 10cm and the refractive index is 1.5. If the plano surface is silvered, then the focal length will be.
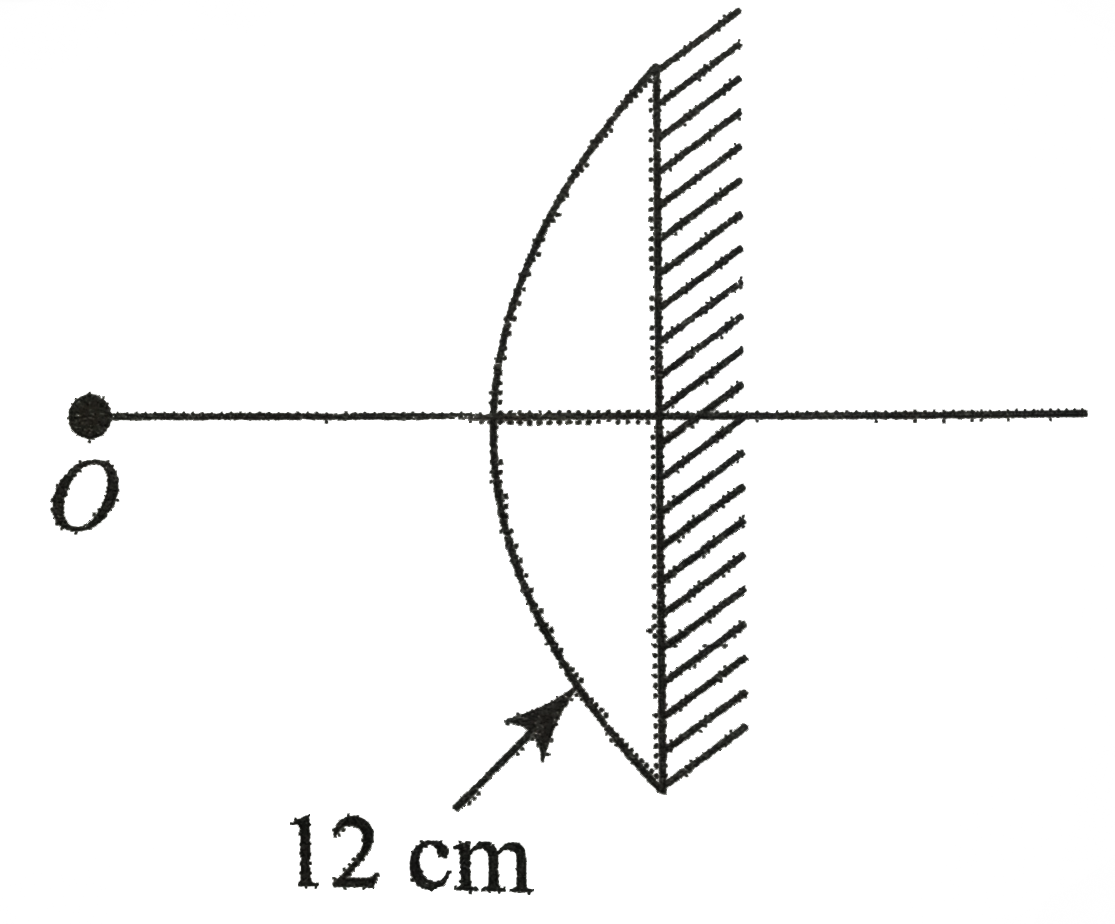
View SolutionA plano-convex lens is silvered on its plane side. The radius of curvature of the other face is 12cm and the refractive index of the material of the lens is 1.5. An object is placed 24 cm in front of the silvered lens. Where will the image be formed?
View SolutionThe radii of curvature of the two surfaces of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5. If the lens is concave -convex, then the focal length of the lens is
View SolutionThe radii of curvature of the two surfaces of a lens are 20 cm and 30 cm and the refractive index of the material of the lens is 1.5. If the lens is concave -convex, then the focal length of the lens is
View SolutionA plano-convex lens is made of refractive index of 1.6. The focal length of the lens is
View Solution
