A spherical surface of radius 30 cm separates two transparent media A and B with refractive indices 1'33 and 1.48 respectively. The medium A is on the convex side of the surface. Where should a point object be placed in medium A so that the paraxial rays become parallel after refraction at the surface ?
The correct Answer is:A, B, C
To solve the problem, we need to determine the position of a point object in medium A such that the paraxial rays become parallel after refraction at the spherical surface separating the two media.
1. Identify Given Values:
- Radius of curvature (R) = 30 cm (since the medium A is on the convex side, R is positive).
- Refractive index of medium A (μ1) = 1.33.
- Refractive index of medium B (μ2) = 1.48.
2. Understand the Condition for Parallel Rays:
- For the rays to become parallel after refraction, they must converge to infinity. This means that the image formed (v) is at infinity.
3. Use the Refraction Formula:
- The formula relating the refractive indices and distances is given by:
μ2v−μ1u=μ2−μ1R
- Here, v=∞, so μ2v=0.
4. Substitute the Known Values:
- Substitute the known values into the equation:
0−1.33u=1.48−1.3330
- Simplifying the right side:
0−1.33u=0.1530
- This simplifies to:
−1.33u=0.005
5. Solve for u:
- Rearranging gives:
1.33u=0.005
- Thus,
u=1.330.005=266 cm
- Since we are considering the sign convention, the object distance u will be negative (as per the sign convention for distances measured against the direction of incident light):
u=−266 cm
6. Conclusion:
- The point object should be placed at a distance of 266 cm in medium A from the spherical surface.
Final Answer:
The point object should be placed at −266 cm in medium A.
- Radius of curvature (R) = 30 cm (since the medium A is on the convex side, R is positive).
- Refractive index of medium A (μ1) = 1.33.
- Refractive index of medium B (μ2) = 1.48.
- For the rays to become parallel after refraction, they must converge to infinity. This means that the image formed (v) is at infinity.
- The formula relating the refractive indices and distances is given by:
μ2v−μ1u=μ2−μ1R
- Here, v=∞, so μ2v=0.
- Substitute the known values into the equation:
0−1.33u=1.48−1.3330
- Simplifying the right side:
0−1.33u=0.1530
- This simplifies to:
−1.33u=0.005
- Rearranging gives:
1.33u=0.005
- Thus,
u=1.330.005=266 cm
- Since we are considering the sign convention, the object distance u will be negative (as per the sign convention for distances measured against the direction of incident light):
u=−266 cm
- The point object should be placed at a distance of 266 cm in medium A from the spherical surface.
The point object should be placed at −266 cm in medium A.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:HC VERMA ENGLISHChapter:GEOMETRICAL OPTICSExercise:EXAMPLE
Explore 9 Videos
- GEOMETRICAL OPTICSBook:HC VERMA ENGLISHChapter:GEOMETRICAL OPTICSExercise:Question For short Answer
Explore 18 Videos
- GEOMETRICAL OPTICSBook:HC VERMA ENGLISHChapter:GEOMETRICAL OPTICSExercise:Objective -2
Explore 7 Videos
- GAUSS LAWBook:HC VERMA ENGLISHChapter:GAUSS LAWExercise:Short Question
Explore 7 Videos
- LIGHT WAVESBook:HC VERMA ENGLISHChapter:LIGHT WAVESExercise:Question for short Answer
Explore 11 Videos
Similar Questions
A concave spherical surface of radius of curvature 10cm separates two mediums X and Y of refractive indices 4/3 and 3/2 respectively. Centre of curvature of the surfaces lies in the medium X. An object is placed in medium X.
View SolutionA concave spherical surface of radius of curvature 100 cm separates two media of refractive indices 1.50 and 43. An object is kept in the first medium at a distance of 30 cm from the surface. Calculate the position of the image.
View Solution
Knowledge Check
A convex refracting surface of radius of curvature 20cm separates two media of refractive indices 4/3and1.60. An object is placed in the first medium (μ=4/3) at a distance of 200cm from the refracting surface. Calculate the position of image formed.
A120cmB240cmC100cmD60cm
A convex surface of radius of curvature 40 cm separate two media of refractive indices 43 and 1.50. An object is kept in the first medium at a distance of 20 cm from the surface. Calculate the position of the image.
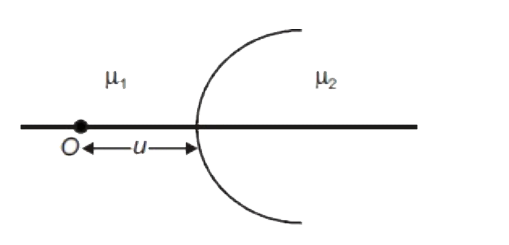
View SolutionA spherical surface of radius R ssparates two media of refractive indices μ1 and μ1 as shown in figure., Where should an object be placed in medium 1 so that a real image is formed in medium 2 at the same distance?
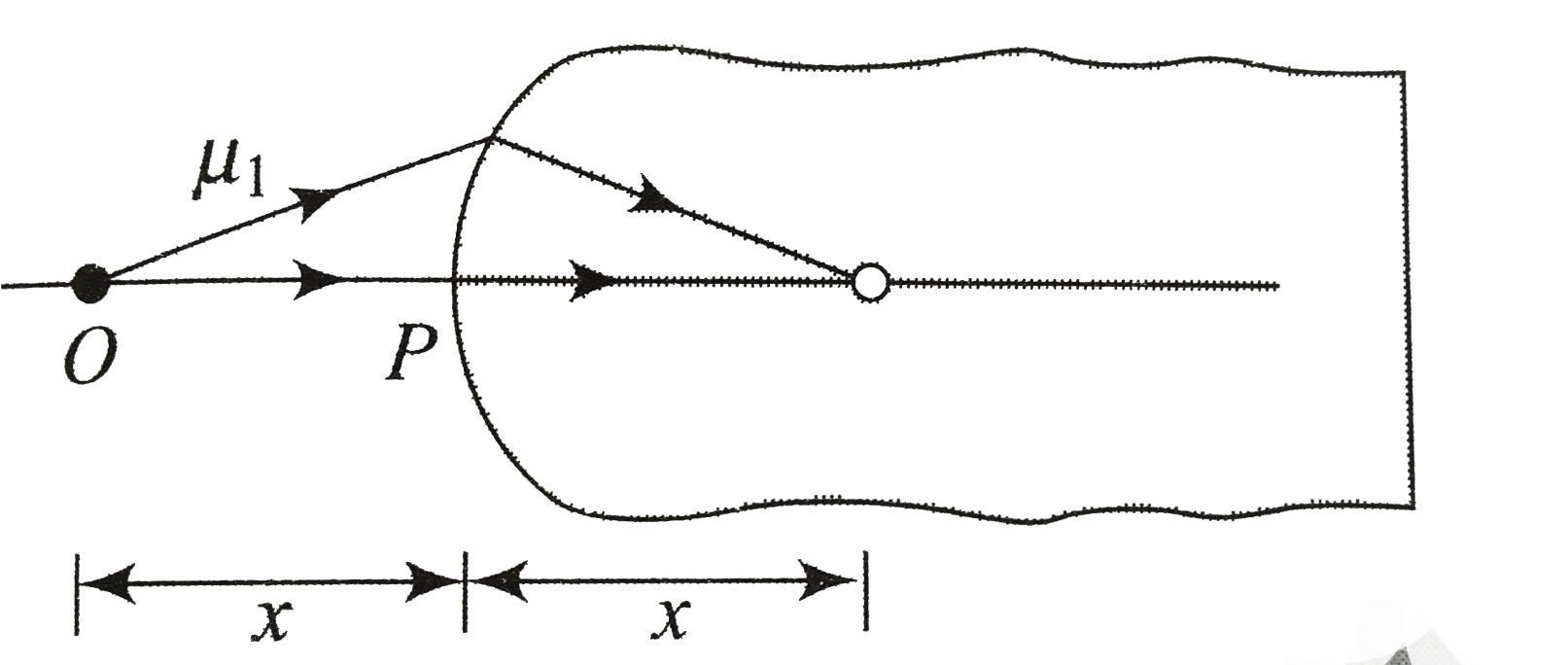
View SolutionThe diagram shows a spherical surface which separates two media of refractive index, μ1andμ2. Respectively. Now, a point object is placed on the principal axis as shown in the figure. Then
View SolutionA curved surface of radius R separates two medium of refractive indices μ1andμ2 as shown in figures A and B .
_E01_078_Q01.png)
Choose the correct statement(s) related to the virtual image formed by object O placed at a distance x, as shown in figure
View SolutionA spherical convex surface separates object and image space of refractive index 1.0and43. If radius of curvature of the surface is 10cm, find its power.
View SolutionA spherical convex surface separates object and image space of refractive index 1.0and43. If radius of curvature of the surface is 10cm, find its power.
View SolutionA curved surface of radius R separates two medium of refractive indices μ1andμ2 as shown in figures A and B .
_E01_077_Q01.png)
Choose the correct statement(s) related to the real image formed by the object O placed at a distance x, as shown in figure A.
View Solution