Question

Light is incident from glass $(\mu =1.5)$ to air. Sketch thevariation of the angle of deviation $\delta$ with angle of incident i for $0<i<{90}^{\circ }$

Answer

A

Explanation

To solve the problem of sketching the variation of the angle of deviation (δ) with the angle of incidence (i) when light travels from glass (with a refractive index μ = 1.5) to air, we can follow these steps:

1. Understanding the Setup:
- Light travels from a denser medium (glass) to a rarer medium (air).
- The refractive index of glass is μ = 1.5.
- The critical angle (c) can be calculated using Snell's law.

2. Calculate the Critical Angle:
- The critical angle (c) can be found using the formula:
\( \sin(c) = \frac{n_2}{n_1} \)
where \( n_1 = 1.5 \) (glass) and \( n_2 = 1.0 \) (air).
- Therefore:
\( \sin(c) = \frac{1.0}{1.5} = \frac{2}{3} \)
- Thus, the critical angle \( c \) is:
\( c = \sin^{-1}\left(\frac{2}{3}\right) \approx 41.81^\circ \)

3. Analyzing the Angle of Deviation:
- The angle of deviation (δ) is defined as:
\( \delta = r - i \)
where \( r \) is the angle of refraction.
- For \( i = 0^\circ \):
- The light travels straight through, so \( \delta = 0^\circ \).
- For \( 0 < i < c \):
- The light refracts into the air, and \( \delta \) increases as \( i \) increases.
- For \( i = c \):
- The angle of refraction \( r = 90^\circ \), hence:
\( \delta = 90^\circ - c \approx 90^\circ - 41.81^\circ \approx 48.19^\circ \)
- For \( i > c \):
- Total internal reflection occurs. The angle of deviation becomes:
\( \delta = 180^\circ - 2i \)
- As \( i \) increases beyond \( c \), \( \delta \) will start decreasing.

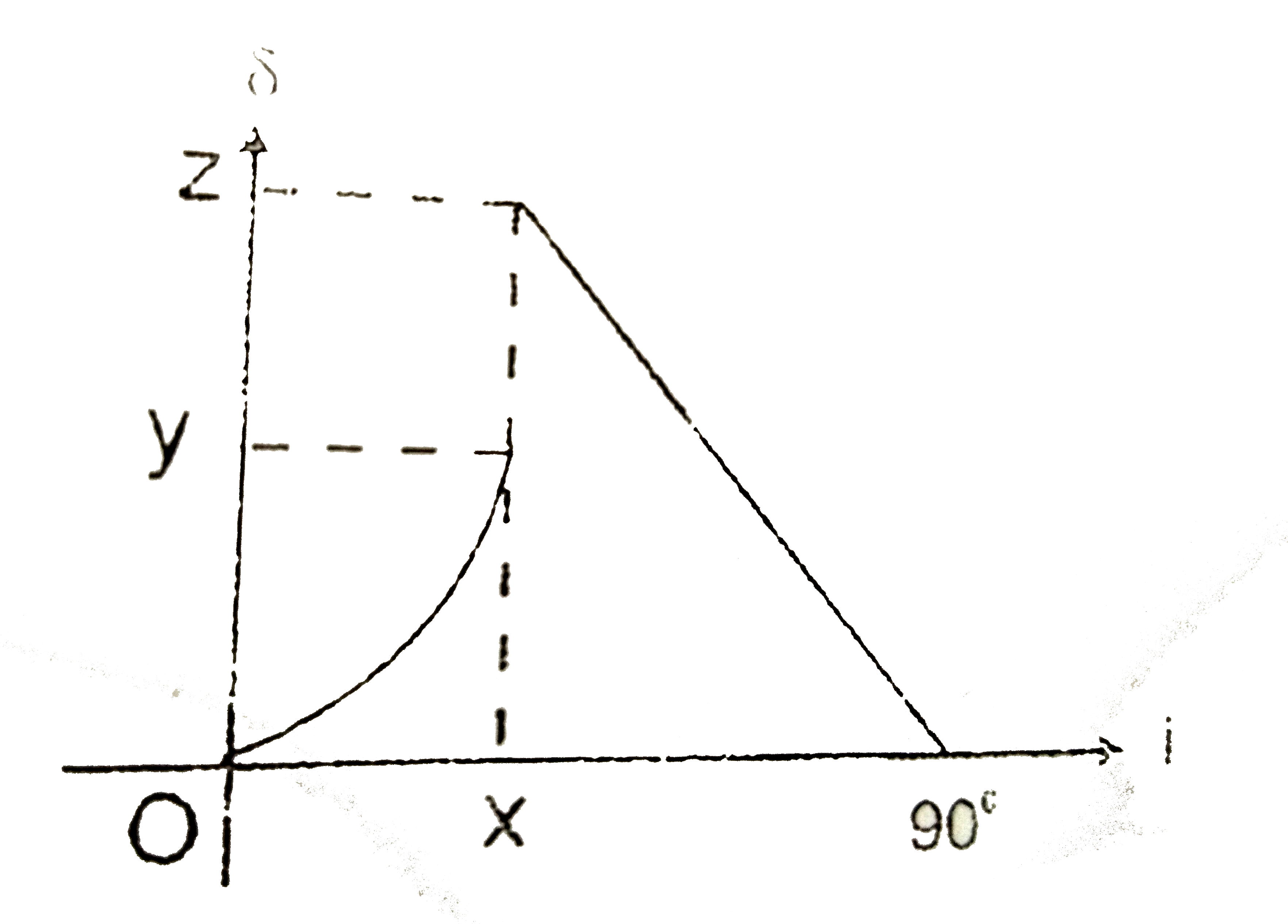
4. Sketching the Graph:
- On the graph, plot \( i \) on the x-axis (from \( 0^\circ \) to \( 90^\circ \)) and \( \delta \) on the y-axis.
- The graph starts at the origin (0,0).
- As \( i \) approaches \( c \), \( \delta \) increases and reaches a maximum value of approximately \( 48.19^\circ \).
- After \( c \), the graph will drop sharply as \( \delta \) decreases due to total internal reflection, continuing to decrease as \( i \) approaches \( 90^\circ \).

Final Graph:
- The graph will have two distinct sections:
1. Increasing Section: From \( (0,0) \) to \( (c, \delta) \).
2. Decreasing Section: From \( (c, \delta) \) to \( (90^\circ, \delta) \).