A uniform meter stick is suspended through a small pin hole at the 10 cm mark. Find the time period of small oscillation about the point of suspension.
To find the time period of small oscillations of a uniform meter stick suspended at the 10 cm mark, we can follow these steps:
Step 1: Identify the Parameters
- The length of the meter stick (L) = 1 meter (100 cm).
- The point of suspension is at the 10 cm mark.
- The center of mass of the meter stick is located at the 50 cm mark (which is at L/2).
Step 2: Calculate the Distance from the Hinge to the Center of Mass
- The distance (d) from the point of suspension (10 cm) to the center of mass (50 cm) is:
d=50cm−10cm=40cm=0.4m
Step 3: Calculate the Moment of Inertia (I)
The moment of inertia (I) of a uniform rod about an axis through one end is given by:
I=13mL2
However, since we are using the parallel axis theorem, we also need to add the term for the center of mass:
I=112mL2+md2
Substituting L=1m and d=0.4m:
I=112m(12)+m(0.42)=112m+m(0.16)=112m+0.16m=(112+0.16)m
Calculating the common denominator:
112+0.16=112+16100=112+48300=25300+48300=73300
Thus,
I=73300m
Step 4: Calculate the Time Period (T)
The formula for the time period T of a physical pendulum is:
T=2π√Imgd
Substituting the values we have:
T=2π
⎷73300mmg(0.4)
The mass m cancels out:
T=2π
⎷73300g⋅0.4
Assuming g≈9.81m/s2:
T=2π√73300⋅0.4⋅9.81
Calculating the denominator:
300⋅0.4⋅9.81=1177.2
Thus,
T=2π√731177.2
Calculating the square root:
T≈2π√0.0619≈2π⋅0.2488≈1.56s
Final Answer
The time period of small oscillations of the meter stick about the point of suspension is approximately 1.56 seconds.
- The length of the meter stick (L) = 1 meter (100 cm).
- The point of suspension is at the 10 cm mark.
- The center of mass of the meter stick is located at the 50 cm mark (which is at L/2).
- The distance (d) from the point of suspension (10 cm) to the center of mass (50 cm) is:
d=50cm−10cm=40cm=0.4m
The moment of inertia (I) of a uniform rod about an axis through one end is given by:
I=13mL2
However, since we are using the parallel axis theorem, we also need to add the term for the center of mass:
I=112mL2+md2
Substituting L=1m and d=0.4m:
I=112m(12)+m(0.42)=112m+m(0.16)=112m+0.16m=(112+0.16)m
Calculating the common denominator:
112+0.16=112+16100=112+48300=25300+48300=73300
Thus,
I=73300m
The formula for the time period T of a physical pendulum is:
T=2π√Imgd
Substituting the values we have:
T=2π
⎷73300mmg(0.4)
The mass m cancels out:
T=2π
⎷73300g⋅0.4
Assuming g≈9.81m/s2:
T=2π√73300⋅0.4⋅9.81
Calculating the denominator:
300⋅0.4⋅9.81=1177.2
Thus,
T=2π√731177.2
Calculating the square root:
T≈2π√0.0619≈2π⋅0.2488≈1.56s
The time period of small oscillations of the meter stick about the point of suspension is approximately 1.56 seconds.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective -1
21 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
15 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
The time period of small oscillations of mass m :-
_S01_040_Q01.png)
View SolutionA uniform semi-circular disc of mass m and radius r is suspended as shown in the figure. If T is the time period of small osciallations about an axis passing through point of supension and perpendicular to plane of disk. Then T is equal to
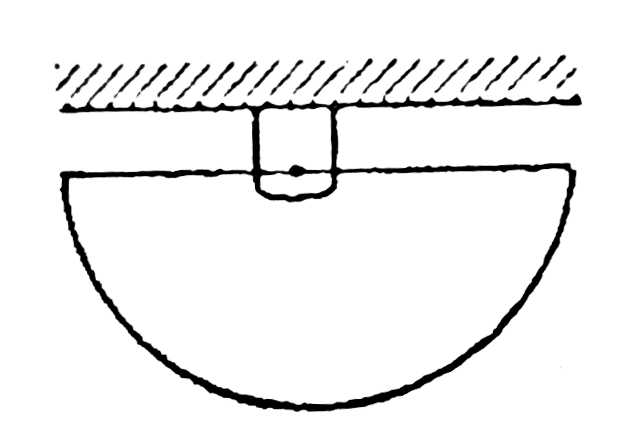
View SolutionA simple pendulum of length l is suspended through the ceiling of an elevator. Find the time period of small oscillations if the elevator a. is going up with an acceleration a0. b. is going down with an acceleration a0 and c. is moving with a uniform velocity.
View SolutionA uniform square plate at side a is hinged at one at its comes it is suspended such than it can rotate about horizontal axis. The time period of small oscillation about its equilibrium position.
View SolutionA uniform disc of mass m and radius r is suspended through a wire attached to its Centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
View SolutionA simple pendulum is suspended from the ceiling a car accelerating uniformly on a horizontal road. If the acceleration is a0 and the length of the pendulum is l, find the time period of small oscillations about the mean position.
View SolutionA solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
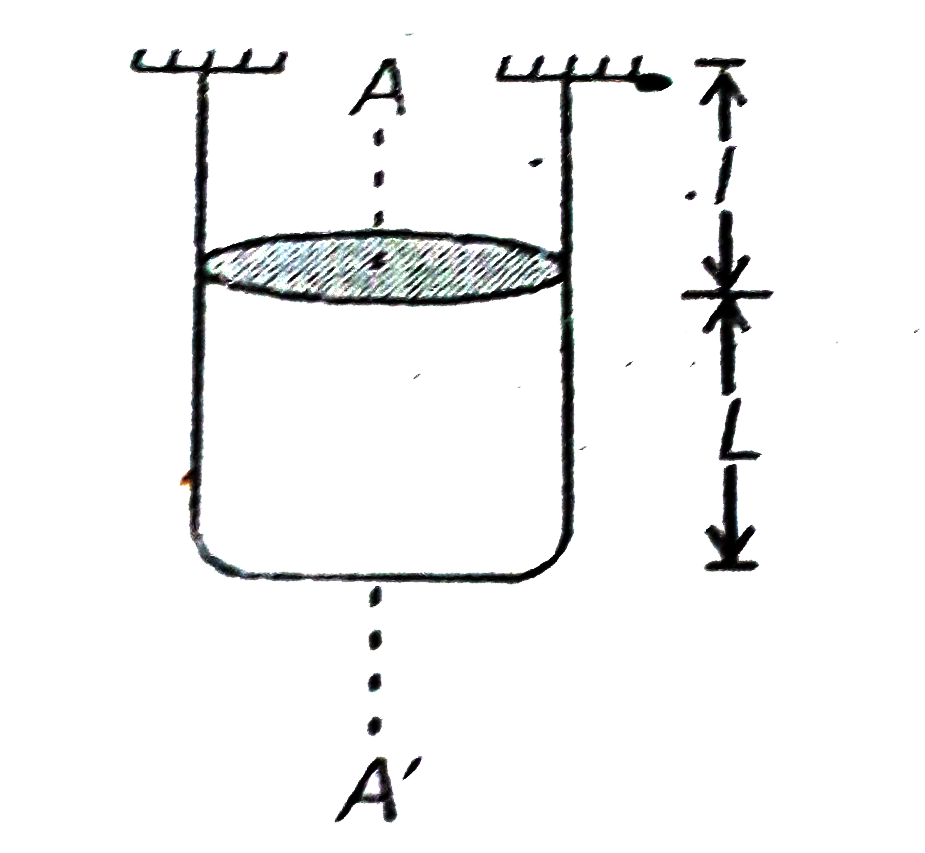
View SolutionA system is shown in the figure. The force The time period for small oscillations of the two blocks will be

View SolutionA uniform rod of length l is suspended from a point P. and the rod is made to undergo small oxcillations. Match the following
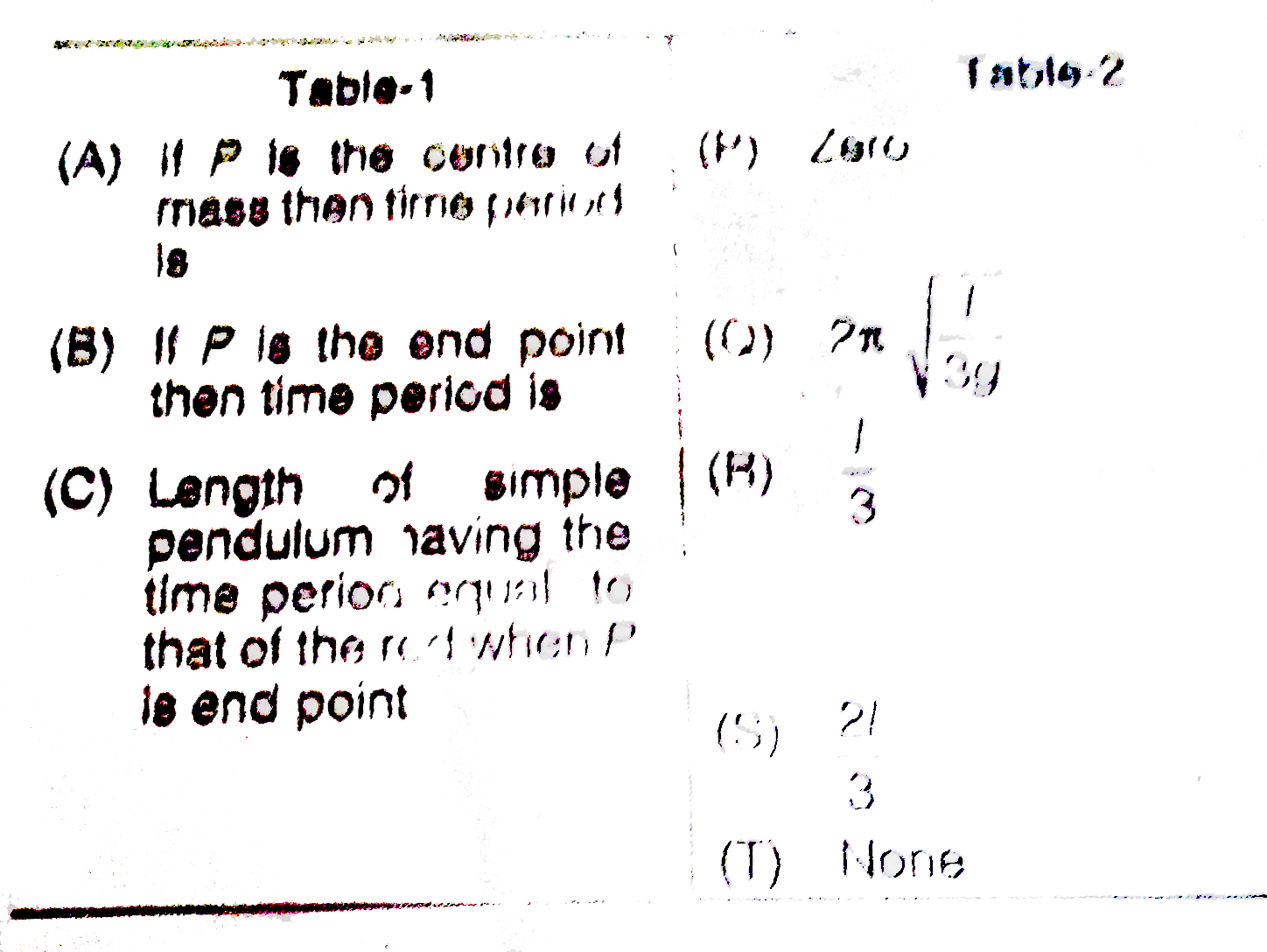
View SolutionFind the time period of m if pulley P is light and small.
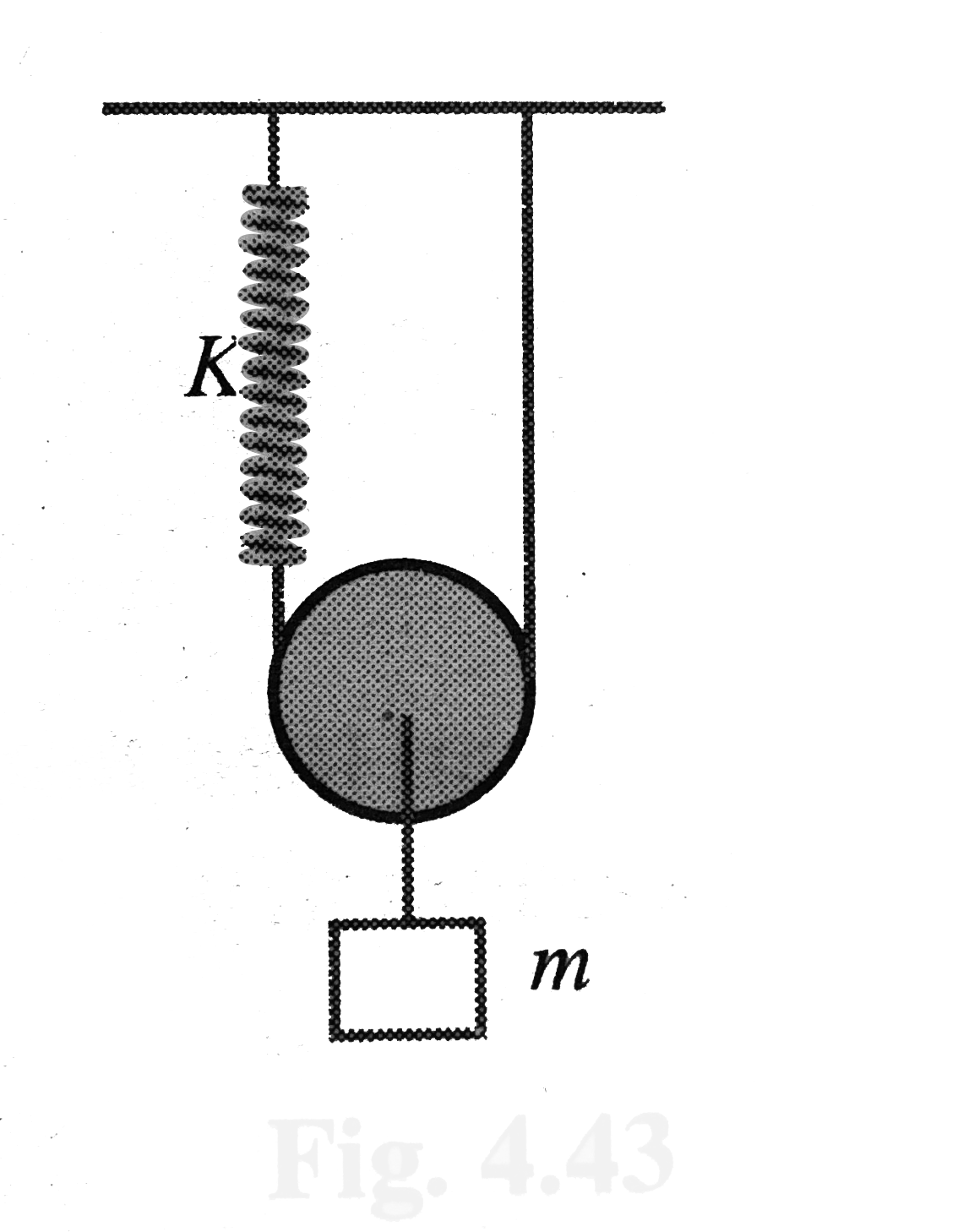
View Solution
