A particle suspended from a vertical spring oscillates 10 times per second. At the highest point of oscillation the spring becomes unstretched. A. Find the maximum speed of the block. B. Find the speed when the spring is stretched by 0.20 cm. Take g=π2ms−2
To solve the problem step by step, we will break it down into parts A and B as requested.
Part A: Finding the Maximum Speed of the Block
1. Identify the frequency and calculate the angular frequency (ω):
- Given frequency f=10Hz.
- The angular frequency ω is calculated using the formula:
ω=2πf=2π×10=20πrad/s
2. Determine the amplitude (A):
- At the highest point of oscillation, the spring becomes unstretched, which means the amplitude A can be calculated using the relationship between gravitational force and spring force.
- The equilibrium position of the spring is given by:
mg=kA
- Rearranging gives:
A=mgk
- We also know from the time period T:
T=2π√mk⟹k=4π2mT2
- Substituting T=1f=110:
k=4π2m×100=400π2m
- Thus:
A=mg400π2m=g400π2
- Given g=π2:
A=π2400π2=1400m=0.0025m=0.25cm
3. Calculate the maximum speed (V_max):
- The maximum speed in simple harmonic motion is given by:
Vmax=Aω
- Substituting the values:
Vmax=0.0025×20π=0.05πm/s
- Converting to cm/s:
Vmax=5πcm/s≈15.7cm/s
Part B: Finding the Speed when the Spring is Stretched by 0.20 cm
1. Use the velocity formula for simple harmonic motion:
- The velocity v at a position x is given by:
v=ω√A2−x2
- Here, x=0.20cm=0.0020m.
2. Substitute the values:
- We already have A=0.0025m and ω=20π:
v=20π√(0.0025)2−(0.0020)2
- Calculate A2−x2:
(0.0025)2=0.00000625,(0.0020)2=0.000004
A2−x2=0.00000625−0.000004=0.00000225
- Therefore:
v=20π√0.00000225=20π×0.0015=0.03πm/s
- Converting to cm/s:
v≈3πcm/s≈9.42cm/s
Final Answers
- A. Maximum Speed: Vmax≈15.7cm/s
- B. Speed when stretched by 0.20 cm: v≈9.42cm/s
- Given frequency f=10Hz.
- The angular frequency ω is calculated using the formula:
ω=2πf=2π×10=20πrad/s
- At the highest point of oscillation, the spring becomes unstretched, which means the amplitude A can be calculated using the relationship between gravitational force and spring force.
- The equilibrium position of the spring is given by:
mg=kA
- Rearranging gives:
A=mgk
- We also know from the time period T:
T=2π√mk⟹k=4π2mT2
- Substituting T=1f=110:
k=4π2m×100=400π2m
- Thus:
A=mg400π2m=g400π2
- Given g=π2:
A=π2400π2=1400m=0.0025m=0.25cm
- The maximum speed in simple harmonic motion is given by:
Vmax=Aω
- Substituting the values:
Vmax=0.0025×20π=0.05πm/s
- Converting to cm/s:
Vmax=5πcm/s≈15.7cm/s
- The velocity v at a position x is given by:
v=ω√A2−x2
- Here, x=0.20cm=0.0020m.
- We already have A=0.0025m and ω=20π:
v=20π√(0.0025)2−(0.0020)2
- Calculate A2−x2:
(0.0025)2=0.00000625,(0.0020)2=0.000004
A2−x2=0.00000625−0.000004=0.00000225
- Therefore:
v=20π√0.00000225=20π×0.0015=0.03πm/s
- Converting to cm/s:
v≈3πcm/s≈9.42cm/s
- A. Maximum Speed: Vmax≈15.7cm/s
- B. Speed when stretched by 0.20 cm: v≈9.42cm/s
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective -121videos
SIMPLE HARMONIC MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-215videos
SIMPLE HARMONIC MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer15videos
SIMPLE HARMONIC MOTION
- BOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer21videos
ROTATIONAL MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-27videos
SOME MECHANICAL PROPERTIES OF MATTER
Similar Questions
Frequency of a particle executing SHM is 10 Hz. The particle is suspended from a vertical spring. At the highest point of its oscillation the spring is unstretched. Maximum speed of the particle is (g=10m/s2
View SolutionA mass is suspended from a vertica spring which is executing SHM of frequency 5 Hz.
The spring is unstretched at the highest point of oscillation. Maximum speed of the mass is (take, acceleration due to gravity, g=10m/s2 )View SolutionA ball of mass 2kg hanging from a spring oscillates with a time period 2π seconds. Ball is removed when it is in equilibrium position, then spring shortens by
View Solution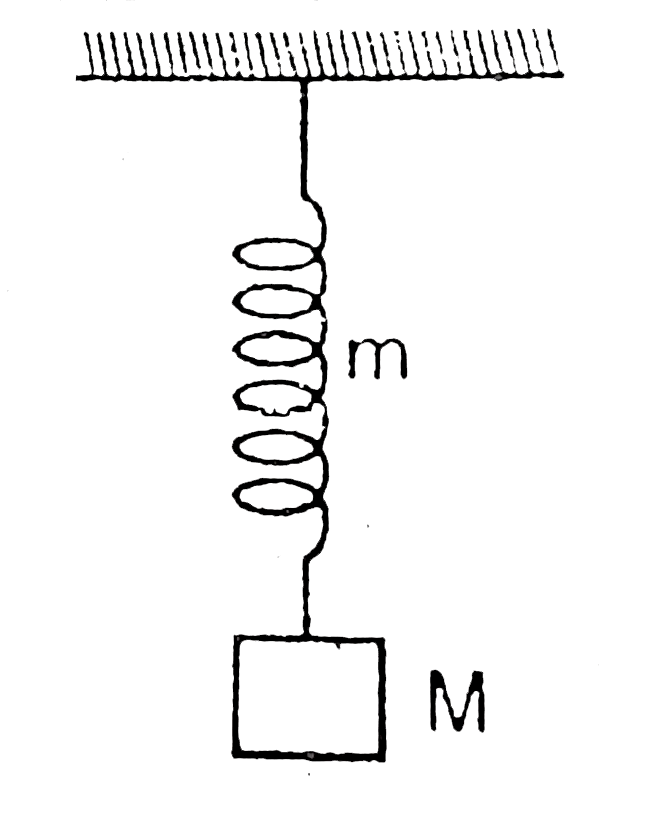
A block of M is suspended from a vertical spring of mass m as shown in the figure. When block is pulled down and released the mass oscillates with maximum velocity v.View SolutionThe pulley shown in figure has a radius of 20 cm and moment of inertial 0.2 kg-m^2. The string going over it is attached at one end to a vertical sprign of spring constant 50 N/m fixed from below and supports a 1 kg mas at other end. The system is released from rest with the spring at its natural length. Find the speed of the block when it has desceds through 10 cm. Take g=10ms2.
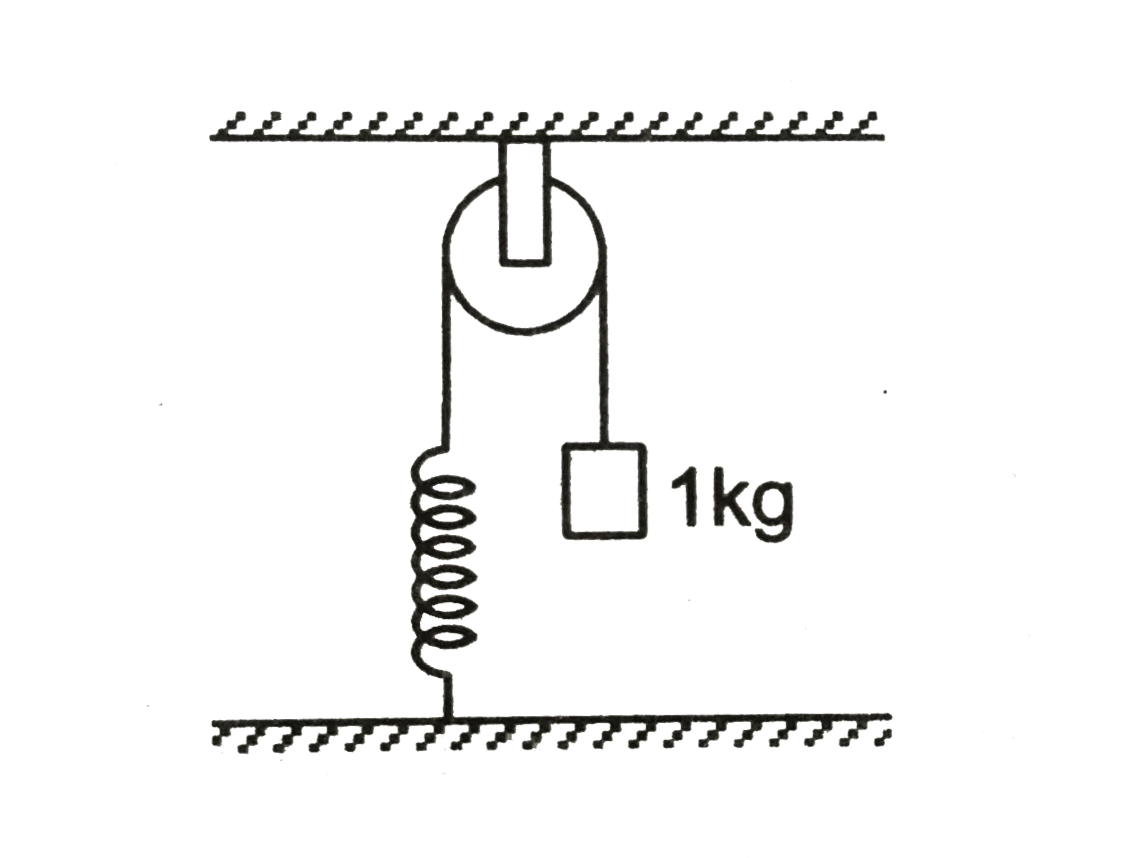 View Solution
View SolutionIn the given arrangement the block is released from the position where the spring is unstretched. The speed of the block when it has descended through 2cm is x10. Find the value of x.
 View Solution
View SolutionA block of mass 0.5 kg hanging from a vertical spring executes simple harmonic motion of amplitude 0.1 m and time period 0.314s. Find the maximum fore exerted by the spring on the blockl.
View SolutionA body of mass 2 kg suspended through a vertical spring executes simple harmonic motionof period 4s. If the oscillations are stopped and the body hangs in equillibrium, find the potential energy stored in the spring.
View SolutionA block of mass m is connected to a massless pulley and mass-less spring of stiffness k. The pulley is frictionless. The string is mass-less. Initially the spring is unstretched when the block is released. When the spring is maximum stretched, find the ratio of tenstion in the rope and weight of the block.
 View Solution
View SolutionTime period of a block with a spring is T0. Now ,the spring is cut in two parts in the ratio 2:3. Now find the time period of same block with the smaller part of the spring.
View Solution
