A 2 kg block iks placed over a 4 kg block and both are plced on a smooth horizontal surfae. The coefficient of friction between the blocks is 0.20. Find theacceleration of the two blocks if a horizontal force os 12 N is applied to a. the upper block, b. the lower block. Take g=10ms2.
To solve the problem, we need to analyze two scenarios where a force is applied to either the upper block or the lower block. We will calculate the accelerations in both cases step by step.
Given Data:
- Mass of upper block (m1) = 2 kg
- Mass of lower block (m2) = 4 kg
- Coefficient of friction (μ) = 0.20
- Applied force (F) = 12 N
- Acceleration due to gravity (g) = 10 m/s²
Step 1: Calculate the maximum frictional force between the blocks
The normal force (N) acting on the upper block (m1) due to its weight is:
N=m1⋅g=2kg⋅10m/s2=20N
The maximum frictional force (f_max) can be calculated using:
fmax=μ⋅N=0.20⋅20N=4N
Step 2: Case (a) - Force applied on the upper block
Assuming both blocks move together, the total mass (M) is:
M=m1+m2=2kg+4kg=6kg
The acceleration (a) if they move together can be calculated using Newton's second law:
F=M⋅a
12N=6kg⋅a
a=126=2m/s2
Now, we need to check if this acceleration is possible with the available friction. The required frictional force (f_required) to keep the blocks moving together is:
frequired=m1⋅a=2kg⋅2m/s2=4N
Since the maximum frictional force (4 N) is equal to the required frictional force (4 N), the blocks can move together.
Step 3: Calculate the acceleration of each block
Now, let's find the acceleration of each block:
- For the upper block (m1):
Fnet=F−fmax=12N−4N=8N
Using Newton's second law:
8N=2kg⋅a1
a1=82=4m/s2
- For the lower block (m2):
The only force acting on it is the frictional force:
fmax=m2⋅a2
4N=4kg⋅a2
a2=44=1m/s2
Summary for Case (a):
- Acceleration of upper block (a1) = 4 m/s²
- Acceleration of lower block (a2) = 1 m/s²
Step 4: Case (b) - Force applied on the lower block
Assuming both blocks move together again, the total mass remains the same (6 kg) and the maximum frictional force is still 4 N.
Calculating the required frictional force to keep them moving together:
frequired=m1⋅a=2kg⋅2m/s2=4N
Since the maximum frictional force (4 N) is equal to the required frictional force (4 N), they can move together.
Step 5: Calculate the acceleration of each block in this case
- For the upper block (m1):
fmax=m1⋅a1
4N=2kg⋅a1
a1=42=2m/s2
- For the lower block (m2):
Fnet=F−fmax=12N−4N=8N
Using Newton's second law:
8N=4kg⋅a2
a2=84=2m/s2
Summary for Case (b):
- Acceleration of upper block (a1) = 2 m/s²
- Acceleration of lower block (a2) = 2 m/s²
Final Answers:
- Case (a): a1 = 4 m/s², a2 = 1 m/s²
- Case (b): a1 = 2 m/s², a2 = 2 m/s²
- Mass of upper block (m1) = 2 kg
- Mass of lower block (m2) = 4 kg
- Coefficient of friction (μ) = 0.20
- Applied force (F) = 12 N
- Acceleration due to gravity (g) = 10 m/s²
The normal force (N) acting on the upper block (m1) due to its weight is:
N=m1⋅g=2kg⋅10m/s2=20N
fmax=μ⋅N=0.20⋅20N=4N
Assuming both blocks move together, the total mass (M) is:
M=m1+m2=2kg+4kg=6kg
F=M⋅a
12N=6kg⋅a
a=126=2m/s2
frequired=m1⋅a=2kg⋅2m/s2=4N
Now, let's find the acceleration of each block:
- For the upper block (m1):
Fnet=F−fmax=12N−4N=8N
Using Newton's second law:
8N=2kg⋅a1
a1=82=4m/s2
The only force acting on it is the frictional force:
fmax=m2⋅a2
4N=4kg⋅a2
a2=44=1m/s2
- Acceleration of upper block (a1) = 4 m/s²
- Acceleration of lower block (a2) = 1 m/s²
Assuming both blocks move together again, the total mass remains the same (6 kg) and the maximum frictional force is still 4 N.
frequired=m1⋅a=2kg⋅2m/s2=4N
- For the upper block (m1):
fmax=m1⋅a1
4N=2kg⋅a1
a1=42=2m/s2
Fnet=F−fmax=12N−4N=8N
Using Newton's second law:
8N=4kg⋅a2
a2=84=2m/s2
- Acceleration of upper block (a1) = 2 m/s²
- Acceleration of lower block (a2) = 2 m/s²
- Case (a): a1 = 4 m/s², a2 = 1 m/s²
- Case (b): a1 = 2 m/s², a2 = 2 m/s²
Topper's Solved these Questions
- FRICTIONBook:HC VERMA ENGLISHChapter:FRICTIONExercise:Questions for short Answer
Explore 11 Videos
- FRICTIONBook:HC VERMA ENGLISHChapter:FRICTIONExercise:Objective -2
Explore 5 Videos
- FLUID MECHANICSBook:HC VERMA ENGLISHChapter:FLUID MECHANICSExercise:All Questions
Explore 90 Videos
- GRAVITATIONBook:HC VERMA ENGLISHChapter:GRAVITATIONExercise:Question for short Answers
Explore 18 Videos
Similar Questions
A 2kg block is placed over a 5kg block and both are placed on a smooth horizontal surface. The coefficient of friction between the blocks is 0.10. Find the acceleration of the two blocks if a horizontal force of 14N is applied to the upper block (g = 10ms−2).
View SolutionA 3 kg block is placed over a 10 kg block and both are palced on a smooth horizontal surface. The coefficient of friction between the block is 0.2 . If a horizontal force of 20 N is applied to 3 kg block, accelerations of the two block in ms−2 are (take, g=ms−2)

View Solution
Knowledge Check
A block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
A10NB5NC2.5ND20NTwo blocks A and B of masses 10 kg and 15 kg are placed in contact with each other rest on a rough horizontal surface as shown in the figure. The coefficient of friction between the blocks and surface is 0.2. A horizontal force of 200 N is applied to block A. The acceleration of the system is (Take g=10ms−2)
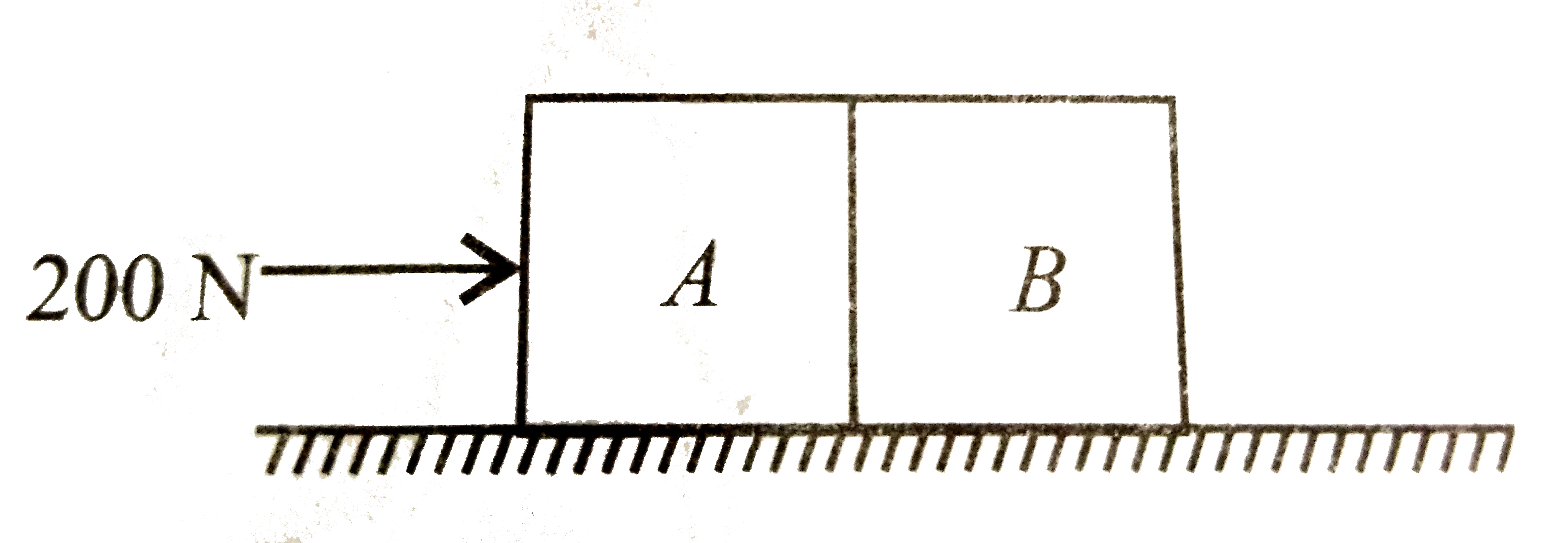 A4ms−2B6ms−2C8ms−2D10ms−2
A4ms−2B6ms−2C8ms−2D10ms−2
A block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
View SolutionA block of mass m is placed on another block of mass M lying on a smooth horizontal surface as shown in the figure. The co-efficient of friction between the blocks is μ. Find the maximum horizontal force F (in Newton) that can be applied to the block M so that the blocks together with same acceleration? (M=3kg,m=2kg,μ=0.1,g=10m/s2)

View SolutionA block A of mass 2kg is placed over smooth block B of mass 4kg which is placed over a smooth horizontal floor The coefficient of friction between A and B is 0.4 when a horizontal forces of magnitude 10N is applied on A the acceleration of block of A and B are

View SolutionA block of mass m is kept over another block of mass 2 m and the system rests on a smooth horizontal surface. The coefficient of friction between the blocks is 0.50. Find the work done by the force of friction on the smaller block by the bigger block during a displacement d of the system, when a force mg is applied to the lower block.
View SolutionA block of massm is placed on another block of mass M which itself is lying on a horizontal surface .The coefficient of friction between two blocks is μ1and that between the block of mass M and horizontal surfece is μ2 What maximum horizontal force can be applied to the lower block move without separation?

View SolutionA block A of mass m kg lies on a block B of mass m kg. B in turn lies on smooth horizontal plane. The coefficient of friction between A and B is μ. Both the blocks are initially at rest. A horizontal force F is applied to lower block B at t = 0 till the lower block B undergoes a displacement of magnitude L. Match the statements in Table-1 with the results in Table-2.

View Solution

