The friction coefficient between a road and the tyre of a vehicle is 4/3. Find the maximum incline the road may thave so that once hard brakes are applied and the wheel starts skidding, the vehicle going down at a speed of 36 km/hr is stopped within 5m.
To find the maximum incline of the road such that a vehicle traveling at 36 km/hr can stop within 5 meters after applying hard brakes, we can follow these steps:
Step 1: Convert the speed from km/hr to m/s
The speed of the vehicle is given as 36 km/hr. To convert this to meters per second (m/s), we use the conversion factor:
Speed in m/s=Speed in km/hr×518
Calculating this gives:
Speed=36×518=10 m/s
Step 2: Determine the required deceleration
We need to find the deceleration required to stop the vehicle within a distance of 5 meters. We can use the third equation of motion:
v2=u2+2as
where:
- v=0 (final velocity),
- u=10 m/s (initial velocity),
- s=5 m (stopping distance),
- a is the deceleration.
Rearranging the equation to solve for a:
0=(10)2+2a(5)⟹0=100+10a⟹10a=−100⟹a=−10 m/s2
Step 3: Set up the forces on the incline
When the vehicle is on an incline, the forces acting on it are:
- The gravitational force component acting down the incline: mgsinθ
- The frictional force acting up the incline: μmgcosθ
Using Newton's second law, we can set up the equation:
μmgcosθ−mgsinθ=ma
Dividing through by m (mass of the vehicle):
μgcosθ−gsinθ=a
Substituting a=−10 m/s² and g≈10 m/s²:
μgcosθ−gsinθ=−10
Step 4: Substitute the values
Given that the coefficient of friction μ=43:
43⋅10cosθ−10sinθ=−10
Dividing the entire equation by 10:
43cosθ−sinθ=−1
Rearranging gives:
43cosθ−sinθ+1=0
Step 5: Multiply through by 3 to eliminate the fraction
4cosθ−3sinθ+3=0
Rearranging gives:
4cosθ−3sinθ=−3
Step 6: Solve for θ
To find θ, we can express this in terms of sine and cosine:
43cosθ−sinθ=−1
This can be interpreted as:
sinθ=4cosθ+3
Using the identity sin2θ+cos2θ=1, we can solve for θ.
Step 7: Find the angle
Using trigonometric identities, we can find that:
θ=53∘−37∘=16∘
Final Answer
The maximum incline the road may have is:
θ=16∘
The speed of the vehicle is given as 36 km/hr. To convert this to meters per second (m/s), we use the conversion factor:
Speed in m/s=Speed in km/hr×518
Calculating this gives:
Speed=36×518=10 m/s
We need to find the deceleration required to stop the vehicle within a distance of 5 meters. We can use the third equation of motion:
v2=u2+2as
where:
- v=0 (final velocity),
- u=10 m/s (initial velocity),
- s=5 m (stopping distance),
- a is the deceleration.
0=(10)2+2a(5)⟹0=100+10a⟹10a=−100⟹a=−10 m/s2
When the vehicle is on an incline, the forces acting on it are:
- The gravitational force component acting down the incline: mgsinθ
- The frictional force acting up the incline: μmgcosθ
μmgcosθ−mgsinθ=ma
Dividing through by m (mass of the vehicle):
μgcosθ−gsinθ=a
Substituting a=−10 m/s² and g≈10 m/s²:
μgcosθ−gsinθ=−10
Given that the coefficient of friction μ=43:
43⋅10cosθ−10sinθ=−10
Dividing the entire equation by 10:
43cosθ−sinθ=−1
Rearranging gives:
43cosθ−sinθ+1=0
4cosθ−3sinθ+3=0
Rearranging gives:
4cosθ−3sinθ=−3
To find θ, we can express this in terms of sine and cosine:
43cosθ−sinθ=−1
This can be interpreted as:
sinθ=4cosθ+3
Using the identity sin2θ+cos2θ=1, we can solve for θ.
Using trigonometric identities, we can find that:
θ=53∘−37∘=16∘
The maximum incline the road may have is:
θ=16∘
Topper's Solved these Questions
- FRICTIONBOOK - HC VERMA ENGLISHCHAPTER - FRICTIONEXERCISE - Questions for short Answer
11 Videos
- FRICTIONBOOK - HC VERMA ENGLISHCHAPTER - FRICTIONEXERCISE - Objective -2
5 Videos
- FLUID MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - All Questions
90 Videos
- GRAVITATIONBOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Question for short Answers
18 Videos
Similar Questions
A car moving at a speed of 36 km/hr is taking a turn on a circular road of radius 50 m. A small wooden plate is kept on the seat with its plane perpendicular to the radius of the circular road figure. A small bock of mass 100 g is kept on the seat which rests against the plate. The friction coefficient between the block and the plate is μ=0.58. a. Find the normal contact force exerted by the plate on the block. b. The plate is slowly turned so that the angle between the normal to the plate and the radius of the road slowly increases Find the angle at which the block will just start sliding on the plate.

View SolutionFigure shown a small block A of mass m kept at the left end of a plank B of mass M=2m and length l . The system can slide on a horizontal road. The system is started towards right with the initial velocity v. The friction coefficient between the road and the plank is 1/2 and that between the plank and the block is 1/4 . Find

(a) the time elapsed before the block separates from the plank
(b) displacement of block and plank relative to ground till that moment.
View Solution
Knowledge Check
The coefficient of friction between the tyres and the road is 0.1. The maximum speed with which a cyclist can take a circular turn of radius 3 m without skidding is (Take g=10ms−2)
A√15ms−1B√3ms−1C√30ms−1D√10ms−1
The coefficient of friction between the tyres and road is 0.4. The minimum distance covered before attaining a speed of 8ms−1 starting from rest is nearly ( take g=10ms−2)
View SolutionThe coefficient of static friction between a block of mass m and an incline is μs=0.3, a. What can be the maximum angle θ of the incline with the horizontal so that the block does not slip on the plane? b. If the incline makes an angle θ2 with the horizontal, find the frictional force on the block.
View SolutionA rectangular box lies on a rough inclined surface . The coefficient of friction between the surface and the box is μ. Let the mass of the box be m .
(a) At what angle of inclination θ of the plane to the horizontal will the box just start to slide down the plane ?
(b) What is the force acting on the box down the plane , if the angle of inclination of the plane is increased to α>θ ?
(c) What is the force needed to be applied upwards along the plane to make the box either remain stationary or just move up with uniform speed ?
(d) What is the force needed to be applied upwards along the plane to make the box move up the plane with acceleration a ?
View SolutionA block of mass 10 kg slides down on an incline 5 m long and 3 m high. A man pushes up on the ice block parallel to the incline so that it slides down at constant speed. The coefficient of friction between the ice and the incline is 0.1. Find :
(a) the work done by the man on the block.
(b) the work done by gravity on the block.
(c) the work done by the surface on the block.
(d) the work done by the resultant forces on the block.
(e) the change in K.E. of the block.
View SolutionA bar of mass m is placed on a triangular block of mass M as shown in figure The friction coefficient between the two surface is μ and ground is smooth find the minimum and maximum horizontal force F required to be applied on block so that the bar will not slip on the inclined surface of block

View SolutionA block of mass 2 kg rests on an inclined plane which makes an angle of 30∘ with the horizontal. The coefficient of friction between the block and the surface is √3/2. (i) What force should be applied on the block so that it moves down without any acceleration ? (ii) What force should be applied on the block so that it moves up without any acceleration ? (iii) Calculate the ratio of the powers in the above two cases if the block moves with uniform speed in both the cases.
View SolutionTwo block tied with a massless string of length 3m are placed on a rotating table as shown. The axis of rotation is 1m from 1kg mass and 2m from 2kg mass. The angular speed ω=4rad/s . Ground below 2kg block is smooth and below 1kg block is rough. (g=10m/s2)
(a) Find tension in the string, force of friction on 1kg block and its direction.
(b) If coefficient of friction between 1kg block and groung is μ=0.8. Find maximum angular speed so that neither of the blocksd slips.
(c) If maximum tension in the string can be 100N , then maximum angular speed so that neither of the blocks slips.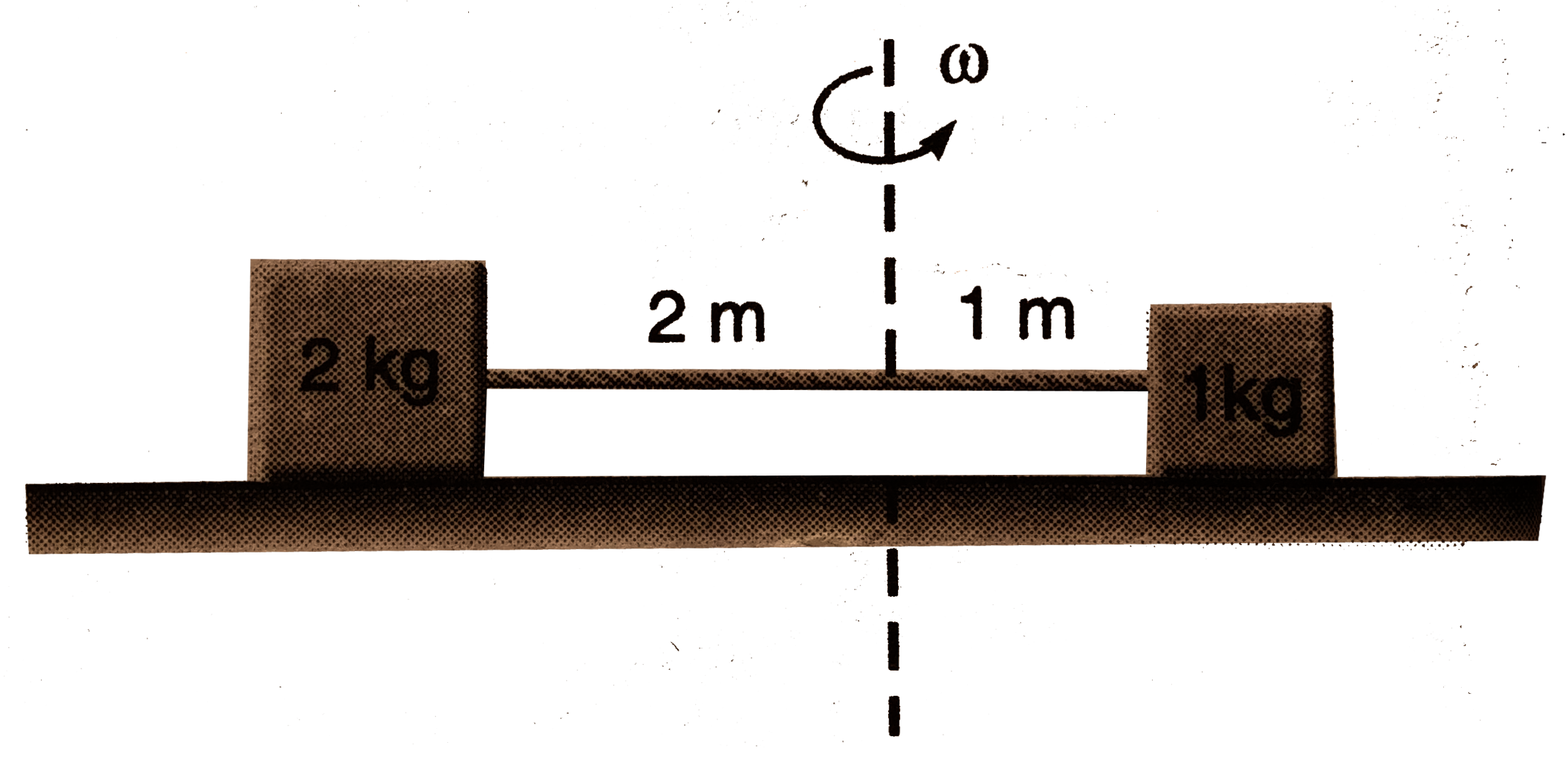
View Solution
